机器学习笔记：非负矩阵分解问题 NMF

Posted 2021-09-28 UQI-LIUWJ

1 NMF介绍

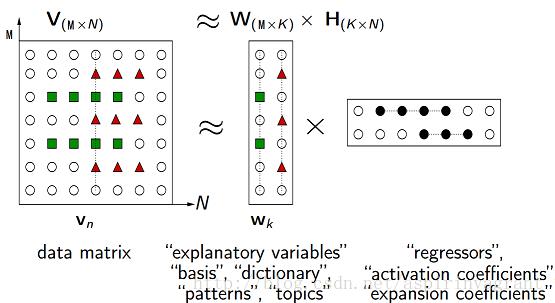
        NMF(Non-negative matrix factorization)，即对于任意给定的一个非负矩阵V，其能够寻找到一个非负矩阵W和一个非负矩阵H，满足条件V=W*H,从而将一个非负的矩阵分解为左右两个非负矩阵的乘积。

        其中，V矩阵中每一列代表一个观测点的信息(observation)，每一行代表一个特征(feature)；W矩阵称为基矩阵，H矩阵称为系数矩阵或权重矩阵。此时V矩阵的每一列，都相当于基矩阵W的每一列对于H矩阵每一列的加权和。

        这时用系数矩阵H代替原始矩阵，就可以实现对原始矩阵进行降维，得到数据特征的降维矩阵，从而减少存储空间。（H的每一个列向量可以看成矩阵V对应的列向量，投影到基矩阵W的每一个列向量得到的坐标）

         NMF本质上说是一种矩阵分解的方法，它的特点是可以将一个大的非负矩阵分解为两个小的非负矩阵，又因为分解后的矩阵也是非负的，所以也可以继续分解。

        非负矩阵分解的关键是“非负”，即原数据和新基底都必须是非负数，或者说位于“第一象限”，这样原数据投影在新基底上的数值才自然也是非负数。

2 用数学语言定义NMF

将矩阵分解问题转换成两个矩阵之间误差最小化的问题

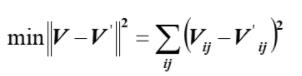
3 W和H的迭代公式

         采用的是迭代法，一步步逼近最终的结果，当计算得到的两个矩阵W和H收敛时，就说明分解成功。

        需要注意的是，原矩阵和分解之后两个矩阵的乘积并不要求完全相等，可以存在一定程度上的误差。

 4 NMF的损失函数

4.0 naive form

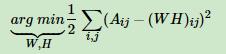
用 矩阵表示，则是：

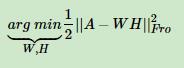
4.1 squared frobenius norm

 

 4.2 KL散度

X,Y分别是原矩阵和WH的乘积结果

4.3  Itakura-Saito (IS)

 5 NMF应用举例

5.1：文本主题模型

假设我们输入有m个词，n个文本。Aij对应的是第i个词在第j个文本的特征值。

经过NMF分解后，Wik对应的是第i个词和第k个“主题”的概率相关度；Hkj对应的是第j个文本和第k个“主题”的概率相关度

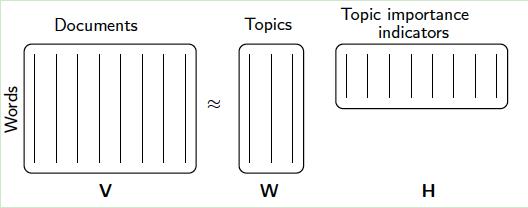
5.2 图像处理

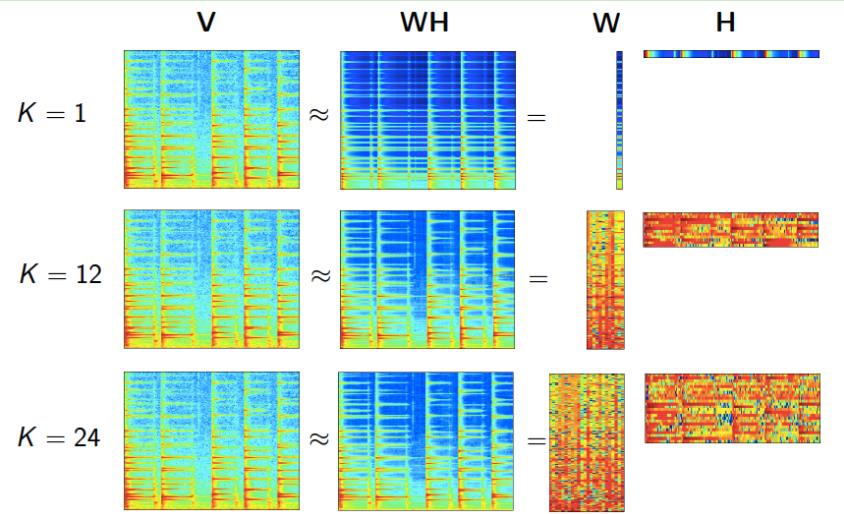
 6 NMF的不足

        NMF作为一个漂亮的矩阵分解方法，它可以很好的用于主题模型，并且使主题的结果有基于概率分布的解释性。

        但是NMF只能对训练样本中的文本进行主题识别，而对不在样本中的文本识别不一定很准确。

文本主题模型之非负矩阵分解(NMF) - 刘建平Pinard - 博客园 (cnblogs.com) 

7 NMF的实现（sklearn）

#导入库
from sklearn.decomposition import NMF
import numpy as np

X = np.array([[1, 1], 
              [2, 1], 
              [3, 1.2], 
              [4, 1], 
              [5, 0.8], 
              [6, 1]])

#定义NMF模型
model = NMF(
    n_components=2, #分解的稠密矩阵中k的大小
    
    beta_loss='frobenius',  
    # {'frobenius', 'kullback-leibler', 'itakura-saito'}
    #对应的是前面说的1~3三种损失函数
    # 一般来说，默认使用naive的损失函数（'frobenius'，同时alpha默认为0）
    
    tol=1e-4,  # 停止迭代的极限条件
    
    init='random',# W H 的初始化方法
    
    max_iter=200,  # 最大迭代次数
    
    l1_ratio=0.,  # L1正则化比例
    
    alpha=0.,  # 正则化参数
    
    random_state=0)

#打印model 构造函数各参数
print(model.get_params())
'''
{'alpha': 0.0, 'beta_loss': 'frobenius', 'init': 'random', 'l1_ratio': 0.0, 'max_iter': 200, 'n_components': 2, 'random_state': 0, 'shuffle': False, 'solver': 'cd', 'tol': 0.0001, 'verbose': 0}
'''

W = model.fit_transform(X)
#相当于model.fit(X) 和 W=model.transform(X) 两步
H = model.components_

print(W,'\\n',H,'\\n',model.n_iter_,'\\n',model.reconstruction_err_)
'''
[[0.         0.46880684]
 [0.55699523 0.3894146 ]
 [1.00331638 0.41925352]
 [1.6733999  0.22926926]
 [2.34349311 0.03927954]
 [2.78981512 0.06911798]]
 
 [[2.09783018 0.30560234]
 [2.13443044 2.13171694]]
 
 30 

 0.0011599349216014024
'''