算法导论习题：摔杯子

Posted 2021-09-28 UQI-LIUWJ

选自Algorithm Design第二章第8题

1 题目描述

        你正在对各种型号的玻璃罐进行一些压力测试，以确定它们可以跌落且不会破裂的高度。

        在特定类型的玻璃罐上，此实验的设置如下：你有一个有 n 个梯级的梯子，你想找到最高的梯级，你可以从那里放下一个罐子，罐子不会摔碎。我们称之为最高的安全梯级。

        尝试二进制搜索可能很自然：从中间的梯级中放一个罐子，看看它是否损坏，然后根据结果从梯级 n/4 或 3n/4 递归尝试。但这有一个缺点，即你可能会在寻找答案时打破很多罐子。

         另一方面，如果您的主要目标是保存罐子，则可以尝试以下策略。首先从第一个梯级放下一个罐子，然后是第二个梯级，依此类推，每次爬高一个，直到罐子破裂。通过这种方式，你只需要一个罐子 在它损坏的那一刻，您就有了正确的答案——但你可能必须将罐子丢n 次（而不是像二进制搜索解决方案中那样记录 n）。

        所以这是一个权衡：如果你愿意打破更多的罐子，你似乎可以执行更少的下降。为了更好地理解这种权衡是如何在定量水平上进行的，让我们考虑如何在给定 k ≥ 1 罐的固定“预算”的情况下运行此实验。换句话说，你必须确定正确的答案——最高的安全梯级——并且在这样做时最多可以使用 k 个罐子。

1.1 问题1

        假设您的预算为 k = 2 罐。 描述一种寻找最高安全梯级的策略，该策略要求您最多丢弃一个罐子 f(n) 次，因为某些函数 f(n) 的增长速度比线性增长慢。 （换句话说，应该是这样的 ）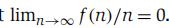

1.2 问题2

        现在假设您有 k > 2 罐的预算，对于某些给定的 k。 描述使用最多 k 个罐子找到最高安全梯级的策略。 如果 fk(n) 表示根据您的策略需要丢弃 jar 的次数，那么函数 f1, f2, f3,... 应该具有这样的特性，即每个函数的增长速度都比前一个慢：  

2 解题思路

2.1 问题1

（1） 假设n是一个安全平方数，我们在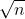的倍数位置上扔第一个罐子，直到它碎了为止

        如果我们到最后一个（也就是n），罐子还没有碎，那么就都是安全高度。

        否则假设它在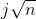的位置碎了，我们就知道最高安全梯级应该在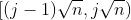之间，于是我们从开始一个一个梯级向上扔，直到碎了为止

        第一个罐子的时间复杂度是

        第二个罐子的时间复杂度也是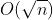

        所以整体的时间复杂度是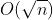

（2）  假设n不是一个安全平方数，我们在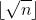的倍数位置上扔第一个罐子，直到它碎了为止(

        否则假设它在的位置碎了，我们就知道最高安全梯级应该在之间，于是我们从开始一个一个梯级向上扔，直到碎了为止

        第一个罐子的时间复杂度是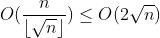

        第二个罐子的时间复杂度是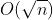

        所以整体的时间复杂度也是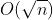

2.2 问题2

        我们假设

        然后我们第一个罐子在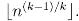以及它的倍数的位置扔下。

        在这种情况下，我们最多扔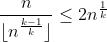,同时，我们把第二个罐子的搜索空间降低至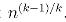

        然后我们递归地看k-1个罐子的情况，根据假设，我们有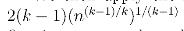，也即

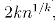 将这个和第一个罐子的情况合并，有：，假设成立