CS224W摘要02.Traditional Methods for Machine Learning in Graphs

Posted 2021-09-27 oldmao_2000

文章目录

• Node-level Tasks and Features
• • Node degree
  • Node centrality
  • Clustering coefficient
  • Graphlets
  • 小结
• Link Prediction Task and Feature
• • Distance-based feature
  • Local neighborhood overlap
  • Global neighborhood overlap
  • • 邻接矩阵的l次方
    • Katz index
• Graph-Level Features and Graph Kernels
• • Graphlet kernel
  • WL kernel

CS224W: Machine Learning with Graphs
公式输入请参考： 在线Latex公式
这节主要从以下三个方面
Node-level prediction
Link-level prediction
Graph-level prediction
以无向图为例，讲解传统的特征工程咋整。

Node-level Tasks and Features

Characterize the structure and position of a node in the network: 有四种

Node degree

用节点度作为特征只计算了相连节点的个数，缺点是没有办法描述节点在图中的重要性。

Node centrality

点度中心性Degree centrality：当前节点的度/（总节点数量-1）
通俗理解就是：重要的节点往往拥有较多连接的节点。你的朋友越多，你的影响力就越强。
特征向量中心性Engienvector centrality：一个节点的邻居节点越重要，那么该节点就越重要。
思想是，我的朋友很重要，那么我就很重要。
那朋友的重要性呢？这就是一个递归计算的问题了。
https://zhuanlan.zhihu.com/p/31198752
这里给了例子，如果是非特征向量与邻接矩阵相乘，就会改变图的点度中心性，只有特征向量不会改变点度中心性，因此求解过程就是求邻接矩阵的特征向量c和特征值$\lambda$。公式不写了，里面的求和项可以转化为邻接矩阵的乘法这里要花心思理解。

中介中心性Betweenness centrality：如果一个节点处于其他节点的多条最短路径上，那么该节点的中心性就高。计算方式：
$$\frac{经过当前节点的最短路径数量}{除了当前节点之外，所有节点对之间的最短路径数量}$$
在社交网络中，该节点往往是中间人的关系，学名是：被禁止的三元组(forbidden triad)的关系
图的边缘节点的中介中心性为0
接近中心性Closeness centrality：如果一个节点跟其他所有节点的距离越近，该节点的中心性就高。计算方式：
$$\frac{1}{当前节点到其他所有节点跳数（路径长度）之和}$$

Clustering coefficient

描述一个图中的节点之间结集成团的程度的系数。例如：社交网络中，我的朋友之间相互认识的程度。

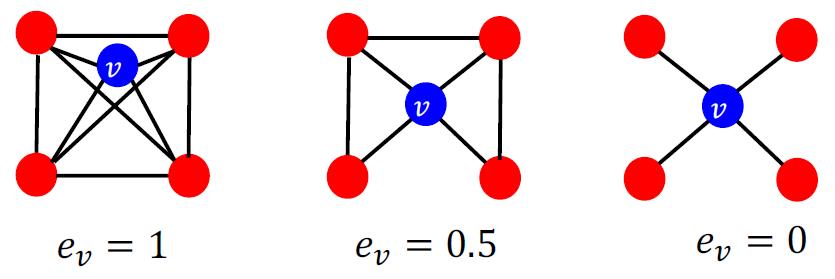
单个节点计算方法：
$$\frac{当前节点的邻居节点之间的边的数量}{当前节点的邻居节点之间的边的最大可能数量}$$
分母实际上是套公式：$\frac{n(n-1)}{2}$
然后求所有节点的平均，得到最后结果。
用例子来说，对于中间的图，v有4个朋友，4个朋友两两组合应该有6个朋友对，但是实际上只有3个朋友对，因此，其聚集系数是3/6=0.5

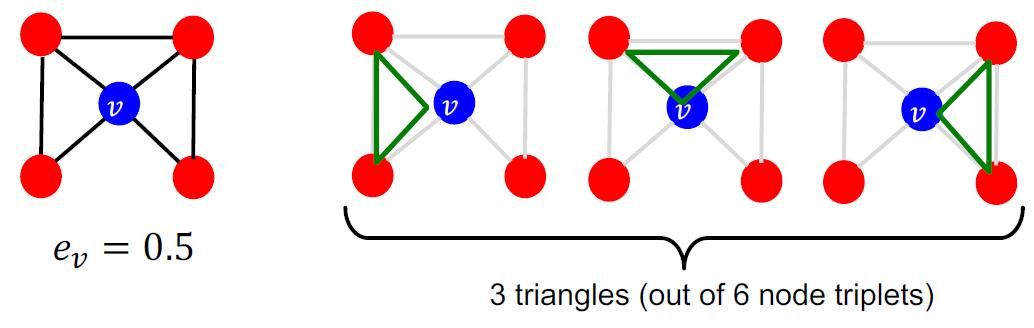
也就是可以数三角形来算。

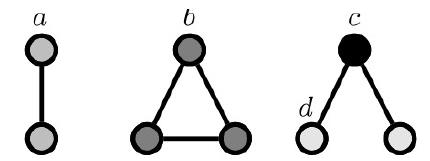
Graphlets

Graphlets: Rooted connected non-isomorphic subgraphs.
graphlets 是一系列连通的非同构子图
ppt中给出不同节点数量的非同构子图，看一小部分即可：

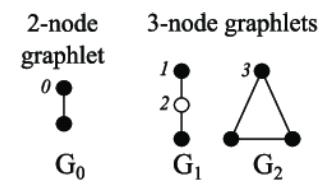
3个节点的时候，$G_1$ 1号和2号节点为根是不同的图，是不同构的。
那么对于下图：

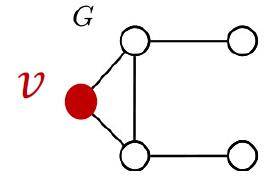
可以包含v的子图有三种，且列出不同构的形态Graph Degree Vector (GDV)，就是能够包含节点v匹配的到的graphlets的个数：

得到Graphlet instances:

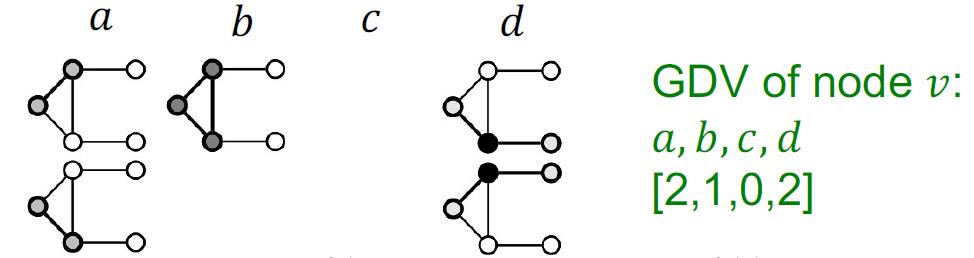
GDV可以用来判定两个结点的局部网络拓扑结构是否类似。

小结

给出了分类
Importance-based features:
§ Node degree
§ Different node centrality measures
可以用于社交网络中的重要人物识别
Structure-based features:
§ Node degree
§ Clustering coefficient
§ Graphlet count vector
可以用于类似固定结构的蛋白质网络预测任务

Link Prediction Task and Feature

把边预测看做任务，一般有两种形式：

1. Links missing at random: Remove a random set of links and then aim to predict them（静态网络如蛋白质网络）
2. Links over time: 预测未来时间步的边的连接情况。（交易网络、社交网络）

训练方法是对节点对之间进行建边评分，然后对评分排序取top n进行建边，并与标签比对。
边特征有三种：

Distance-based feature

用节点间的最短路径作为特征。

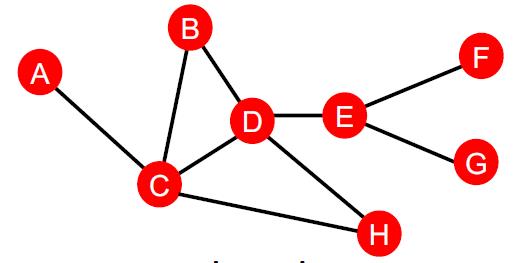
但是这个方法对于领域的特征表示并不明显，例如上图中BH和DF的长度一样，但是BH之间有两条路径而DF只有一条。

Local neighborhood overlap

用两个节点之间的共同邻居数量作为特征。
$$|N(v_1)\cap N(v_2)|$$
归一化的表达，Jaccard’s coefficient:
$$\frac{|N(v_1)\cap N(v_2)|}{|N(v_1)\cup N(v_2)|}$$
这样减少了邻居多少的影响。
进一步对社交网络而言，还进一步衡量了共同邻居的重要度，Adamic-Adar index:：
$$\sum _{u\in N(v_1)\cap N(v_2)}\frac{1}{\log (k_u)}$$

这个衡量方式有缺点：当两个点之间没有共同邻居（$|N(v_1)\cap N(v_2)|=\varphi$）则该特征为0，但是实际上二者未来还是可能有边的。例如上图中的节点A和E，二者从图中看是有间接关系，但是Local neighborhood overlap没法表示这种关系。

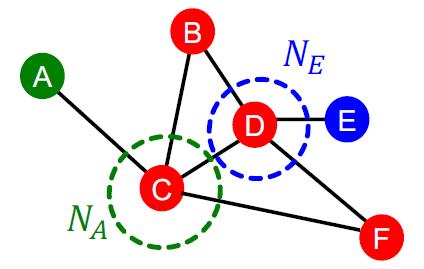
Global neighborhood overlap

解决上面的问题。

邻接矩阵的l次方

count the number of paths of all lengths between a given pair of nodes.
计算上面的number的方法就求邻接矩阵的乘方。
例如：计算距离为1的节点,，因为邻接矩阵本身就是表示相邻节点的，所以表示为：$A^{(1)}$;
计算距离为2的节点：$A^{(2)}$简单理解就是：u到v长度为2的路径数量，先找u到i（长度为1），再找i到v（长度为1）,累加，看上去貌似很复杂，其实就是写成邻接矩阵相乘：
$$\sum _i{A}_{ui}\times A_{iv}=A_{uv}^2$$
例子：

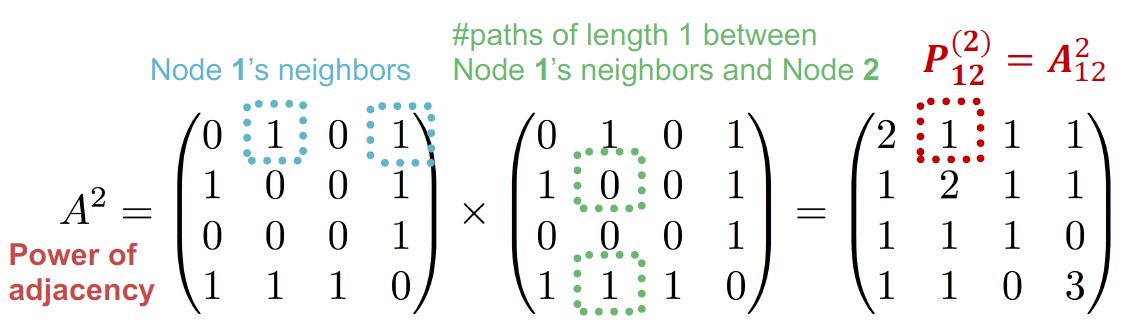
上面表明节点1到2有长度为2的路径：1→4→2
那么通过归纳法：邻接矩阵的$l$次方$A_{uv}^l$可以表示两节点间路径长度为$l$的数量

Katz index

两个节点$v_1,v_2$之间的Katz index可以表示为：
$$S_{v_1{v}_2}=\sum _{l=1}^{\infty }{\beta }^l{A}_{v_1{v}_2}^l$$
这里$0<\beta <1$是长短路径不同的权重（这里长路径的权重要低一些）
Katz index可以写成（矩阵级数的计算）：
$$S_{v_1{v}_2}=\sum _{i=1}^{\infty }{\beta }^i{A}^i=(I-$$

CS224W摘要总纲（已完结）

CS224W摘要10.Knowledge Graph Embeddings

CS224W摘要03.Node Embedding

CS224W摘要05.Message passin and Node classification

CS224W摘要15.Deep Generative Models for Graphs