《LeetCode之每日一题》:145.x 的平方根

Posted 2021-09-27 是七喜呀！

x的平方根

• 有关题目
• • 题解

有关题目

给你一个非负整数 x ，计算并返回 x 的 平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。

注意：不允许使用任何内置指数函数和算符，
例如 pow(x, 0.5) 或者 x ** 0.5 。

示例 1：

输入：x = 4
输出：2

示例 2：

输入：x = 8
输出：2
解释：8 的平方根是 2.82842..., 由于返回类型是整数，
小数部分将被舍去。

提示：

0 <= x <= 2^31 - 1

题解

法一：袖珍计算器算法
参考官方题解

思路：
使用指数函数exp 与对数函数ln 代替平方根函数

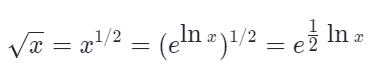
细节：
①
2147395600 = 46,340 * 46,340，但在exp 与 ln函数运算中，
由于自然对数e是一个无限不循环小数，其值约等于2.718281828459…，
我们只能得出一个与答案非常靠近但小于答案的近似值，故我们需要在此验证(ans + 1) * (ans + 1) 与 x 之间的关系
②
我们注意到题干条件给的x 的范围 0 <= x <= 2^31 - 1
当我们的x = INT_MAX时，在验证答案的时候可能会溢出，
故验证的时候我们需要强制类型转换一下

class Solution {
public:
    int mySqrt(int x) {
        if (x == 0) return 0;
        int ans = exp(0.5 * log(x));
        return ((long long)(ans + 1) * (ans + 1) <= x ? ans + 1 : ans);
    }
};

法二：二分查找

思路：
由于题干条件需要我们找到x 的平方根，加上取整，
故需要找到满足条件mid * mid <= x，我们的最大mid整数值
我们可以通过二分查找加速这一查找过程

class Solution {
public:
    int mySqrt(int x) {
        int l = 0, r = x, ans = -1;
        while(l <= r){
            int mid = l + (r - l) / 2;
            if ((long long)mid * mid <= x){
                ans = mid;
                l = mid + 1;
            }
            else {
                r = mid - 1;
            }
        }
        return ans;
    }
};

时间复杂度：O(log x)，即为二分查找的次数
空间复杂度：O(1)

法三：牛顿迭代法
牛顿迭代法

思路：牛顿迭代法可以近似快速求解函数零点
构建函数y = x ^ 2 - C（其中C 为输入数据）
使用牛顿迭代法来求解零点

细节：
①
注意寻找x(i) 与 x(i+1)之间的关系
②
注意构建函数时，对于本题来说，由于我们寻找的为零点中较大值，
所以我们使用找 x0时也要从x ^ (1/2)右边来找，这里x0取输入值
③
一般来说当 x(i) 与 x(i+1)之间的查找小于1e-7时，我们就可以得到自己想要的答案了

class Solution {
public:
    int mySqrt(int x) {
        if (x == 0) return 0;

        double C = x, x0 = x;
        while(x0 * x0 > x){//while(true)也可
            double x1 = 0.5 * (x0 + C / x0);
            if (fabs(x1 - x0) <  1e-7)
                break;
            x0 = x1;
        }
        return (int)x0;
    }
};

时间复杂度：O(log x)，牛顿迭代法二次收敛，比二分查找更快
空间复杂度：O(1)