机器学习笔记03：Normal equation与梯度下降的比较

Posted 2023-03-04 xietx1995

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了机器学习笔记03：Normal equation与梯度下降的比较相关的知识，希望对你有一定的参考价值。

在《机器学习笔记02》中已经讲了多变量的梯度下降法，以及其他的一些小技巧和注意事项。下面来讲一种更加数学化的方法，我们称之为Normal equation，网上也没找到什么标准的翻译，就暂且称其为矩阵方程法吧。

一、简单回顾梯度下降

如下图所示，我们在进行梯度下降的时候，一般都会执行多次迭代，才能得出最佳的一组 $\\theta$ 值。

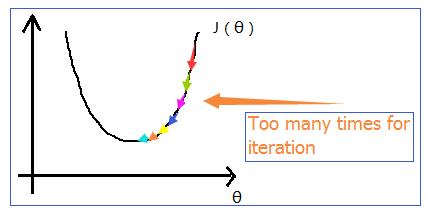
我们能不能只用一次数学意义上的计算就能把所有的

θ $\\theta$ 值都求出来呢，答案是可以的，我们用到的就是 normal equation（矩阵方程法）。

先来看看单元变量的Normal equation方法:

1.当 $\\theta\\in R$ 时，误差函数为

J(θ)=aθ2+bθ+c $J(\\theta)=a\\theta^2+b\\theta+c$ 此时只需要很简单地对

θ $\\theta$ 求导数，使其导数为

0 $0$ 即可求出

θ $\\theta$ ：

Let∂∂θJ(θ)=0 $Let \\quad \\frac\\partial\\partial\\thetaJ(\\theta)=0$
2.当

θ∈Rn+1 $\\theta\\in R^n+1$ 时，误差函数为

J(θ0,θ1,...,θn)=12m∑i=1m(hθ(x(i))−y(i))2 $J(\\theta_0,\\theta_1,...,\\theta_n)=\\frac12m \\sum_i=1^m (h_\\theta(x^(i))-y^(i))^2$ 我们只要对每个

θ $\\theta$ 求偏导数，并使其为

0 $0$ 即可求出每个

θ $\\theta$ 的值：

Let∂∂θjJ(θ)=0(j=0,1,2,...,n) $Let \\quad \\frac\\partial\\partial\\theta_jJ(\\theta)=0 \\quad(j=0,1,2,...,n)$ 这种方法是不是很简单。

我们来看个已经用烂了的例子：房价预测
假设我们有如下的训练数据（样本数量 $m=4$ ,特征数量 $n=4$ ）

	Size( $feet^2$ )	Number of bedrooms	Number of floors	Age of house(years)	Price( $\\$$ 1000)
$x_0$	$x_1$	$x_2$	$x_3$	$x_4$	$y$
1	2104	5	1	45	460
1	1416	3	2	40	232
1	1534	3	2	30	315
1	852	2	1	36	178

我们记X=⎡⎣⎢⎢⎢⎢11112104141615348525332122145403036⎤⎦⎥⎥⎥⎥;y=⎡⎣⎢⎢⎢⎢[ML]简单的Normal Equation对数据点进行线性回归