用Python实现基于遗传算法(GA)求解混合流水车间调度问题(HFSP)
Posted 码丽莲梦露
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了用Python实现基于遗传算法(GA)求解混合流水车间调度问题(HFSP)相关的知识,希望对你有一定的参考价值。
之前一直研究的是柔性作业车间调度问题,研究汇总如下:
用python实现基于遗传算法求解柔性作业车间调度问题代码实现(包括标准算例准换、编码、解码、交叉、变异的详细讲述)
用python实现基于蚁群算法求解带准备时间的双资源约束柔性作业车间调度问题
用Python实现带运输时间准备时间的MSOS染色体解码(FJSP)
Tensorflow2.0|基于深度强化学习(DQN)实现动态柔性作业车间调度问题(DFJSP)
用Python实现论文《考虑装卸的柔性作业车间双资源调度问题》的降准解码算法
今天,来讲述并一下HFSP问题,并给出相应的代码实现。
1 问题描述
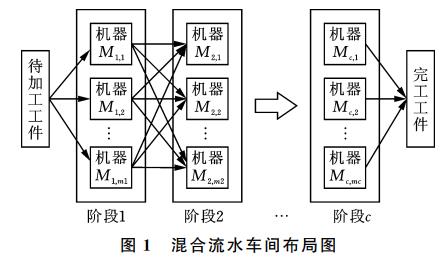
混合流水车间(又称柔性流水车间)在流水车间的基础上,在所有或部分阶段引入多台可选择的并行机器,提高了车间地生产能力和柔性,是车间调度领域研究的热点之一。HFSP问题可以描述为:n 个工件在(c≥2)个阶段上进行连续加工,阶段i有mi(mi ≥1;i=1,2,...,c)台机器,且至少存在一个阶段有多台机 器.HFSP需要根据各阶段上工件的加工顺序和机器分配,来优化某项或多项性能指标.图1为HFSP车间布局图.
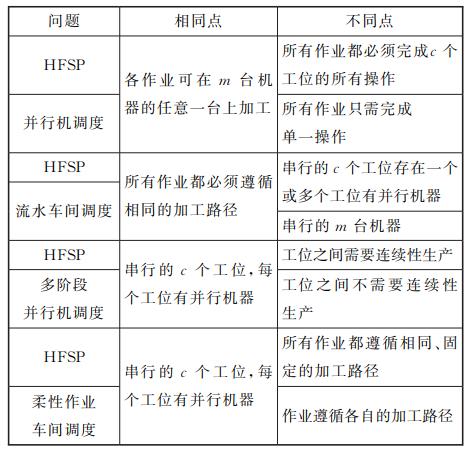
HFSP与其他问题的区别:
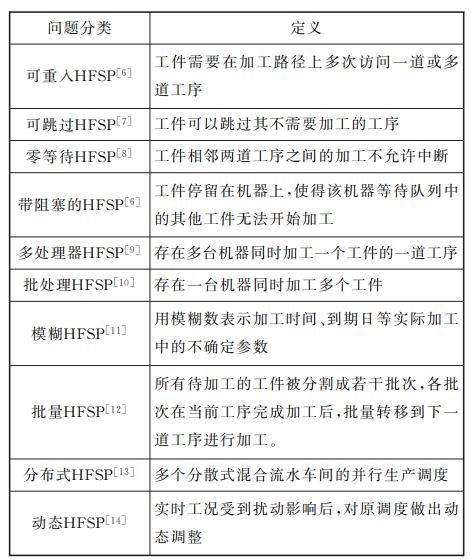
扩展HFSP的分类与定义:
HFSP常用的目标函数:
(1)完工时间
(2)流经时间
(3)工件延迟
(4)工作负荷
(5)总能耗
... ...
本文的目标函数为:最小化完工时间
2 算法
遗传算法对于入门是非常有好的,其他类似进化算法几乎都是在此基础上演变的,当你懂得遗传算法的逻辑和思路以后,上手其他算法就很快了,所以还是本文还是决定用遗传算法来求解。
2.1 初始化
2.1.1 编码
目前大多数求解 HFSP的算法都采用的是基于工件排 列的编码方法,即用 犖 个工件排成顺序队列,工件在队列 中的位置标明工件第一道工序的加工顺序。鉴于后续阶段 工件的加工受上一阶段影响较大,也采用此方法,后续阶段 则根据前一阶段工件加工完成时间采用非降序排列的方式 进行编码。举例说明,例如5个工件的编码 为(4,2,5,1, 3),此编码标明在第一加工阶段,工件4先加工,紧接着工 件2加工、其次是5、再是1、最后是工件3加工。若它们在 第一阶段加工完成到达第二阶段的顺序依次为2、5、4、1、3, 则在 第 二 阶 段 的 编 码 为 (2,5,4,1,3),后 续 阶 段 的 编 码 同理。
2.1.2 解码
对于上述编方法,采用如下解码算法可以构造一个调度方案 :
步骤 1 对每个工件每道工序的所有可用机器计算当前工序的开始时间、完成时间 、加工时间和当前机器负载。计算工序的开始时间时,需要比较该工件上道工序的完成时间 (TP)和该机器 所加工的上道工序的完成时间(TM)。若TM≥TP,且在该机器上TP与TM之间存在大于该工序加工 时间的空隙,则可将该工序插入空隙内,开始时间为空隙中前一道工序的结束时间;若TM<TP,则开始时间为TP。
步骤2 选择机器。优取原则为:优先选取完成时间最小的机器;若完成时间相同,则选取当前机器负载最小的机器;若机器负载也都相同,则随机选取机器。即优先级为完成时间>机器负载 。
步骤3 判断是否所有工件的所有工序都已进行机器选择。若已选择 ,则结束循环,输出调度方案;否则,返回步骤1.
交叉方式:POX
变异:打乱互换
3 代码
3.1 Instance
import random
random.seed(32)
#State:阶段,即工件有几道工序,Job:工件数,Machine['type':list],对应各阶段的并行机数量
def Generate(State,Job,Machine):
PT=[]
for i in range(State):
Si=[] #第i各加工阶段
for j in range(Machine[i]):
S0=[random.randint(1,20) for k in range(Job)]
Si.append(S0)
PT.append(Si)
return PT
Job=20
State=5
Machine=[3,3,2,3,3]
PT=Generate(State,Job,Machine)3.2 Scheduling
import random
import matplotlib.pyplot as plt
from Instance import Job,State,Machine,PT
import numpy as np
class Item:
def __init__(self):
self.start=[]
self.end=[]
self._on=[]
self.T=[]
self.last_ot=0
self.L=0
def update(self,s,e,on,t):
self.start.append(s)
self.end.append(e)
self._on.append(on)
self.T.append(t)
self.last_ot=e
self.L+=t
class Scheduling:
def __init__(self,J_num,Machine,State,PT):
self.M=Machine
self.J_num=J_num
self.State=State
self.PT=PT
self.Create_Job()
self.Create_Machine()
self.fitness=0
def Create_Job(self):
self.Jobs=[]
for i in range(self.J_num):
J=Item()
self.Jobs.append(J)
def Create_Machine(self):
self.Machines=[]
for i in range(len(self.M)): #突出机器的阶段性,即各阶段有哪些机器
State_i=[]
for j in range(self.M[i]):
M=Item()
State_i.append(M)
self.Machines.append(State_i)
#每个阶段的解码
def Stage_Decode(self,CHS,Stage):
for i in CHS:
last_od=self.Jobs[i].last_ot
last_Md=[self.Machines[Stage][M_i].last_ot for M_i in range(self.M[Stage])] #机器的完成时间
last_ML = [self.Machines[Stage][M_i].L for M_i in range(self.M[Stage])] #机器的负载
M_time=[self.PT[Stage][M_i][i] for M_i in range(self.M[Stage])] #机器对当前工序的加工时间
O_et=[last_Md[_]+M_time[_] for _ in range(self.M[Stage])]
if O_et.count(min(O_et))>1 and last_ML.count(last_ML)>1:
Machine=random.randint(0,self.M[Stage])
elif O_et.count(min(O_et))>1 and last_ML.count(last_ML)<1:
Machine=last_ML.index(min(last_ML))
else:
Machine=O_et.index(min(O_et))
s, e, t=max(last_od,last_Md[Machine]),max(last_od,last_Md[Machine])+M_time[Machine],M_time[Machine]
self.Jobs[i].update(s, e,Machine, t)
self.Machines[Stage][Machine].update(s, e,i, t)
if e>self.fitness:
self.fitness=e
#解码
def Decode(self,CHS):
for i in range(self.State):
self.Stage_Decode(CHS,i)
Job_end=[self.Jobs[i].last_ot for i in range(self.J_num)]
CHS = sorted(range(len(Job_end)), key=lambda k: Job_end[k], reverse=False)
#画甘特图
def Gantt(self):
fig = plt.figure()
M = ['red', 'blue', 'yellow', 'orange', 'green', 'moccasin', 'purple', 'pink', 'navajowhite', 'Thistle',
'Magenta', 'SlateBlue', 'RoyalBlue', 'Aqua', 'floralwhite', 'ghostwhite', 'goldenrod', 'mediumslateblue',
'navajowhite','navy', 'sandybrown']
M_num=0
for i in range(len(self.M)):
for j in range(self.M[i]):
for k in range(len(self.Machines[i][j].start)):
Start_time=self.Machines[i][j].start[k]
End_time=self.Machines[i][j].end[k]
Job=self.Machines[i][j]._on[k]
plt.barh(M_num, width=End_time - Start_time, height=0.8, left=Start_time, \\
color=M[Job], edgecolor='black')
plt.text(x=Start_time + ((End_time - Start_time) / 2 - 0.25), y=M_num - 0.2,
s=Job+1, size=15, fontproperties='Times New Roman')
M_num += 1
plt.yticks(np.arange(M_num + 1), np.arange(1, M_num + 2), size=20, fontproperties='Times New Roman')
plt.ylabel("机器", size=20, fontproperties='SimSun')
plt.xlabel("时间", size=20, fontproperties='SimSun')
plt.tick_params(labelsize=20)
plt.tick_params(direction='in')
plt.show()
#
# Sch=Scheduling(J_num,Machine,State,PT)
3.3 GA
import random
import numpy as np
import copy
from Scheduling import Scheduling as Sch
from Instance import Job,State,Machine,PT
import matplotlib.pyplot as plt
class GA:
def __init__(self,J_num,State,Machine,PT):
self.State=State
self.Machine=Machine
self.PT=PT
self.J_num=J_num
self.Pm=0.2
self.Pc=0.9
self.Pop_size=100
# 随机产生染色体
def RCH(self):
Chromo = [i for i in range(self.J_num)]
random.shuffle(Chromo)
return Chromo
# 生成初始种群
def CHS(self):
CHS = []
for i in range(self.Pop_size):
CHS.append(self.RCH())
return CHS
#选择
def Select(self, Fit_value):
Fit = []
for i in range(len(Fit_value)):
fit = 1 / Fit_value[i]
Fit.append(fit)
Fit = np.array(Fit)
idx = np.random.choice(np.arange(len(Fit_value)), size=len(Fit_value), replace=True,
p=(Fit) / (Fit.sum()))
return idx
# 交叉
def Crossover(self, CHS1, CHS2):
T_r = [j for j in range(self.J_num)]
r = random.randint(2, self.J_num) # 在区间[1,T0]内产生一个整数r
random.shuffle(T_r)
R = T_r[0:r] # 按照随机数r产生r个互不相等的整数
# 将父代的染色体复制到子代中去,保持他们的顺序和位置
H1=[CHS1[_] for _ in R]
H2=[CHS2[_] for _ in R]
C1=[_ for _ in CHS1 if _ not in H2]
C2=[_ for _ in CHS2 if _ not in H1]
CHS1,CHS2=[],[]
k,m=0,0
for i in range(self.J_num):
if i not in R:
CHS1.append(C1[k])
CHS2.append(C2[k])
k+=1
else:
CHS1.append(H2[m])
CHS2.append(H1[m])
m+=1
return CHS1, CHS2
# 变异
def Mutation(self, CHS):
Tr = [i_num for i_num in range(self.J_num)]
# 机器选择部分
r = random.randint(1, self.J_num) # 在变异染色体中选择r个位置
random.shuffle(Tr)
T_r = Tr[0:r]
K=[]
for i in T_r:
K.append(CHS[i])
random.shuffle(K)
k=0
for i in T_r:
CHS[i]=K[k]
k+=1
return CHS
def main(self):
BF=[]
x=[_ for _ in range(self.Pop_size+1)]
C=self.CHS()
Fit=[]
for C_i in C:
s=Sch(self.J_num,self.Machine,self.State,self.PT)
s.Decode(C_i)
Fit.append(s.fitness)
best_C = None
best_fit=min(Fit)
BF.append(best_fit)
for i in range(self.Pop_size):
C_id=self.Select(Fit)
C=[C[_] for _ in C_id]
for Ci in range(len(C)):
if random.random()<self.Pc:
_C=[C[Ci]]
CHS1,CHS2=self.Crossover(C[Ci],random.choice(C))
_C.extend([CHS1,CHS2])
Fi=[]
for ic in _C:
s = Sch(self.J_num, self.Machine, self.State, self.PT)
s.Decode(ic)
Fi.append(s.fitness)
C[Ci]=_C[Fi.index(min(Fi))]
Fit.append(min(Fi))
elif random.random()<self.Pm:
CHS1=self.Mutation(C[Ci])
C[Ci]=CHS1
Fit = []
Sc=[]
for C_i in C:
s = Sch(self.J_num, self.Machine, self.State, self.PT)
s.Decode(C_i)
Sc.append(s)
Fit.append(s.fitness)
if min(Fit)<best_fit:
best_fit=min(Fit)
best_C=Sc[Fit.index(min(Fit))]
BF.append(best_fit)
plt.plot(x,BF)
plt.show()
best_C.Gantt()
if __name__=="__main__":
g=GA(Job,State,Machine,PT)
g.main()
4 实验结果
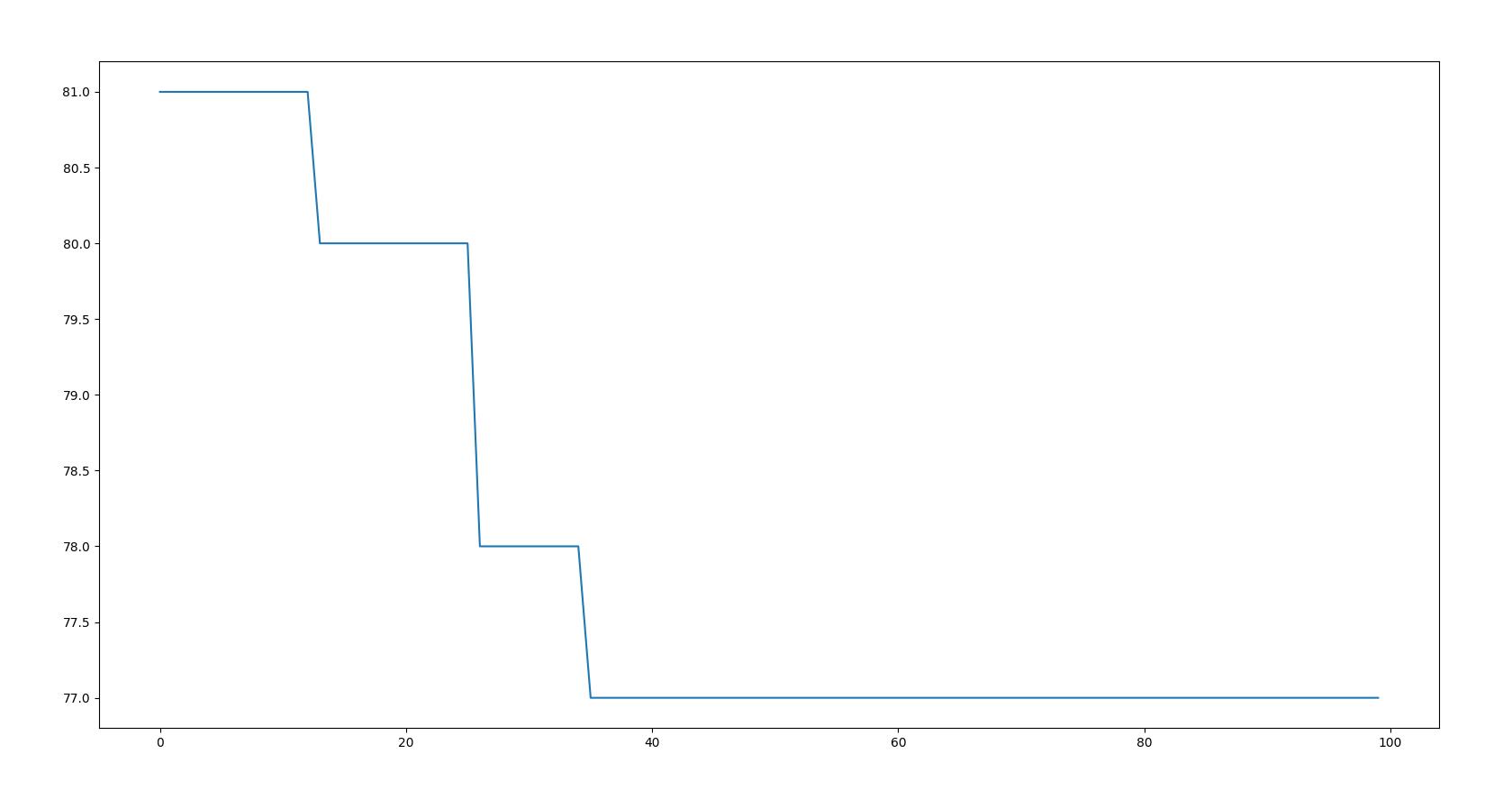
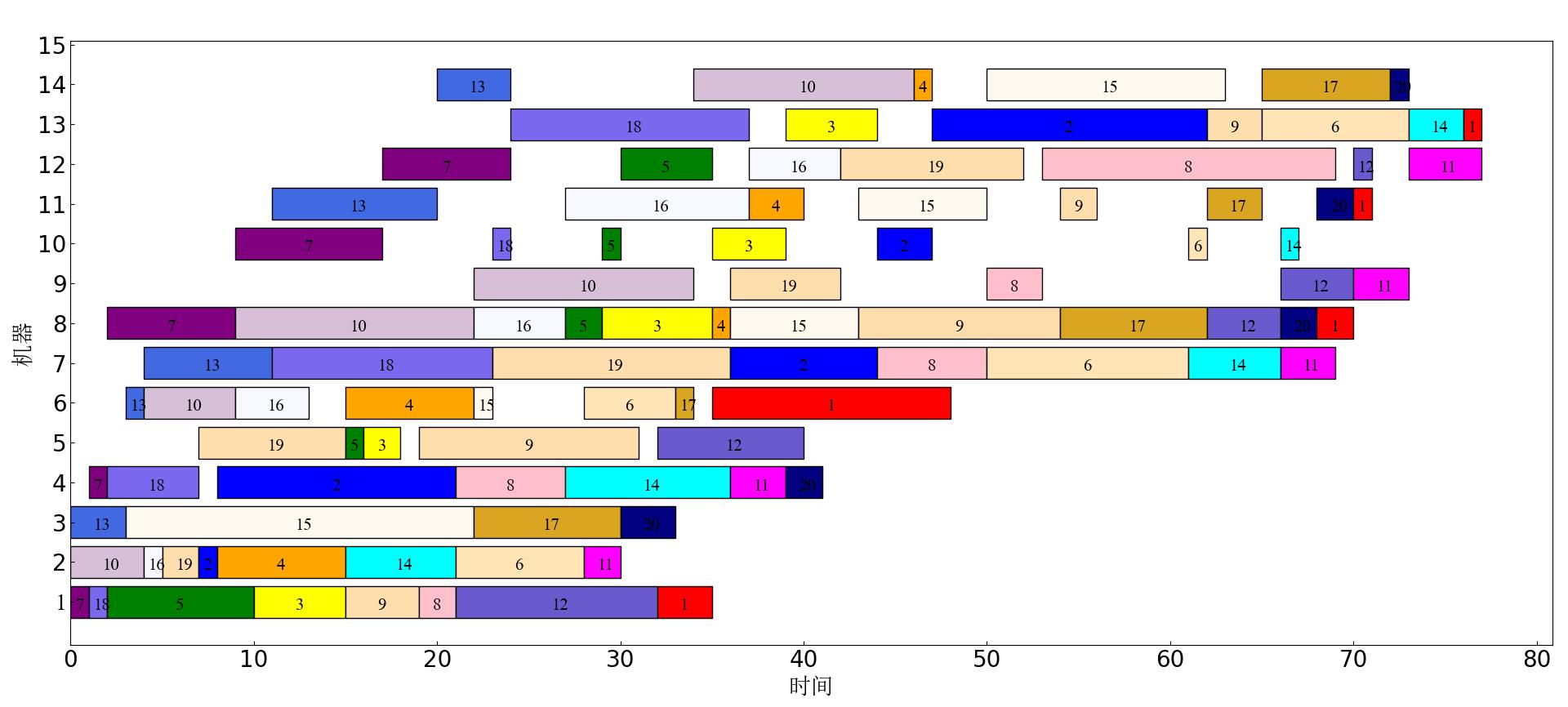
以上是关于用Python实现基于遗传算法(GA)求解混合流水车间调度问题(HFSP)的主要内容,如果未能解决你的问题,请参考以下文章