❤️思维导图整理大厂面试高频数组: 两万字详解各种数组求和(建议收藏)❤️

Posted 孤柒

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了❤️思维导图整理大厂面试高频数组: 两万字详解各种数组求和(建议收藏)❤️相关的知识，希望对你有一定的参考价值。

此专栏文章是对力扣上算法题目各种方法的总结和归纳, 整理出最重要的思路和知识重点并以思维导图形式呈现, 当然也会加上我对导图的详解.

目的是为了更方便快捷的记忆和回忆算法重点(不用每次都重复看题解), 毕竟算法不是做了一遍就能完全记住的. 所以本文适合已经知道解题思路和方法, 想进一步加强理解和记忆的朋友, 并不适合第一次接触此题的朋友(可以根据题号先去力扣看看官方题解, 然后再看本文内容).

关于本专栏所有题目的目录链接, 刷算法题目的顺序/注意点/技巧, 以及思维导图源文件问题请点击此链接.

想进大厂, 刷算法是必不可少的, 欢迎和博主一起打卡刷力扣算法, 博主同步更新了算法视频讲解 和 其他文章/导图讲解, 更易于理解, 欢迎来看!

文章目录

一.你还在用暴力法解 两数之和 吗? 力扣1详细注解

题目链接: https://leetcode-cn.com/problems/two-sum/

0.导图整理

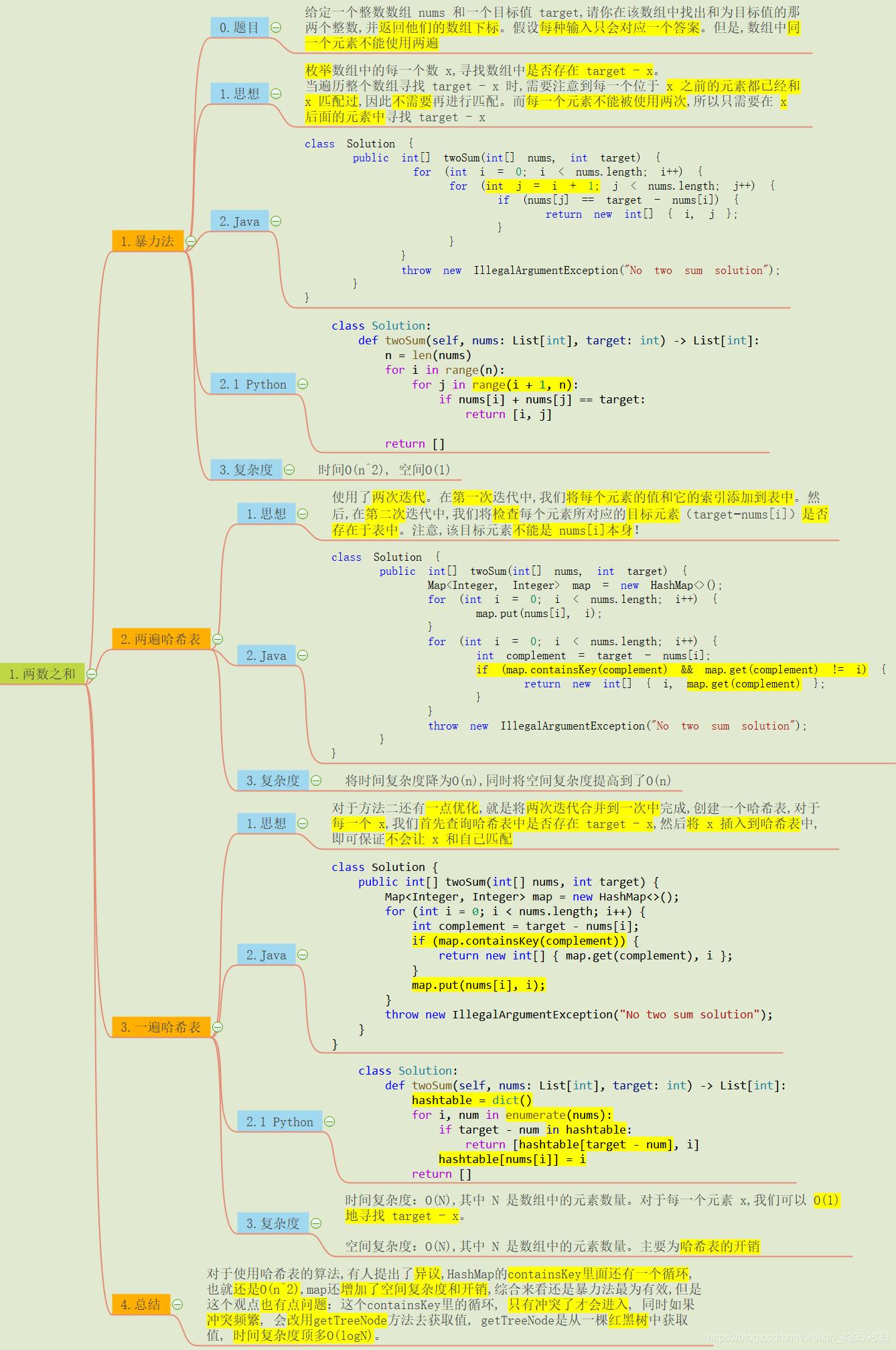
1.暴力法

暴力法的思想很简单, 就是两层循环: 一层用来遍历所有元素, 另一层用来寻找目标数.

但此题中的注意点是题目中的: 假设每种输入只会对应一个答案. 但是, 数组中同一个元素不能使用两遍.

每种输入只对应一个输出 也就是要求我们找到满足的元素直接返回就可以了, 并不需要再去找其他满足的元素, 这也为下面使用哈希表的方法提供了前提, 因为如果需要找到所有满足的元素, 那么哈希表的结构就不能满足要求了.

数组中同一个元素不能使用两遍 这个要求就是代码中标注重点的部分 j = i + 1; 的含义. 当遍历整个数组寻找 target - x 时, 需要注意到每一个位于 x 之前的元素都已经和 x 匹配过, 因此不需要再进行匹配. 而每一个元素不能被使用两次, x本身也不需要进行匹配, 所以只需要在 x 后面的元素中寻找 target - x, 也就是从i+1开始遍历.

2.两遍哈希表

暴力法使用了两层循环, 时间复杂度达到了O(n^2), 而使用哈希表就可以将寻找目标数的操作降为O(1), 直接降了一个量级, 具体过程如下:

使用了两次迭代。在第一次迭代中, 将每个元素的值和它的索引添加到表中。然后, 在第二次迭代中, 检查每个元素所对应的目标元素（target−nums[i]）是否存在于表中。注意, 该目标元素不能是 nums[i]本身！也就是 map.get(complement) != i 的含义.

3.一遍哈希表

对于上面方法还有一点优化, 就是将两次迭代合并到一次中完成, 先进行匹配, 再插入到哈希表中!

首先创建一个哈希表, 对于每一个 x, 首先查询哈希表中是否存在 target - x, 如果存在直接返回结果就可以了. 之后将 x 插入到哈希表中, 即可保证不会让 x 和自己匹配, 因为在匹配时, x还未插入到哈希表中.

这种优化对于时间复杂度没有太大影响, 但是代码看起来更简洁了.

4.哈希表中的循环和异议

对于使用哈希表的算法, 有人提出了异议, HashMap的containsKey里面还有一个循环, 也就还是O(n^2), map还增加了空间复杂度和开销, 综合来看还是暴力法最为有效, 但是这个观点也有点问题: 这个containsKey里的循环, 只有冲突了才会进入, 同时如果冲突频繁, 会改用getTreeNode方法去获取值, getTreeNode是从一棵红黑树中获取值, 时间复杂度顶多O(logN), 综合来看, 还是降低了时间复杂度.

5.java和Python中哈希表的差别

从上述代码可以看出, 两者对于哈希表的实现还是有很大的差别的.

首先java中的哈希表是用Map类实现的, 判断是否包含一个元素用的是 map.containsKey(Key) 函数, 获取 键 对应的 值 使用的是 map.get(Key) 函数, 插入到哈希表中使用的是 map.put(Key, Value)

但是在Python中直接使用它自带的数据类型 字典dict 就实现了哈希表的操作, 并不需要新建类, 而且相应的操作也非常简单, 几乎不需要通过其他函数来实现. 判断是否包含一个元素用的是 in, 获取 键 对应的 值 使用的是 hashtable[Key] 函数, 插入到哈希表中使用的是 hashtable[Key] = Value

仔细对比会发现, Python语法是真的简洁明了, 这也是博主喜欢Python的原因.

这里补充说明一下Python中的 enumerate(nums) 函数, 简单来说就是对nums数组中的所有数添加了下标, 它返回的是 由下标和数据构成的二元元组, 在Python的for循环中还是挺经常使用的函数.

源码

Python:

# 暴力法
class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        n = len(nums)
        for i in range(n):
            for j in range(i + 1, n):
                if nums[i] + nums[j] == target:
                    return [i, j]
 
        return []
 
 
# 一遍哈希表
class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        hashtable = dict()
        for i, num in enumerate(nums):
            if target - num in hashtable:
                return [hashtable[target - num], i]
            hashtable[nums[i]] = i
        return []

java:

// 暴力法
class Solution {
    public int[] twoSum(int[] nums, int target) {
         for (int i = 0; i < nums.length; i++) {
            for (int j = i + 1; j < nums.length; j++) {
                if (nums[j] == target - nums[i]) {
                    return new int[] { i, j };
                }
            }
        }
        throw new IllegalArgumentException("No two sum solution");
    }
}
 
//两遍哈希表
class Solution {
    public int[] twoSum(int[] nums, int target) {
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            map.put(nums[i], i);
        }
        for (int i = 0; i < nums.length; i++) {
            int complement = target - nums[i];
            if (map.containsKey(complement) && map.get(complement) != i) {
                return new int[] { i, map.get(complement) };
            }
        }
        throw new IllegalArgumentException("No two sum solution");
    }
}
 
//一遍哈希表
class Solution {
    public int[] twoSum(int[] nums, int target) {
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            int complement = target - nums[i];
            if (map.containsKey(complement)) {
                return new int[] { map.get(complement), i };
            }
            map.put(nums[i], i);
        }
        throw new IllegalArgumentException("No two sum solution");
    }
}

二.两数之和II有序数组, 多个有序, 思路全变, 力扣167详细注解

题目链接: https://leetcode-cn.com/problems/two-sum-ii-input-array-is-sorted/

0.导图整理

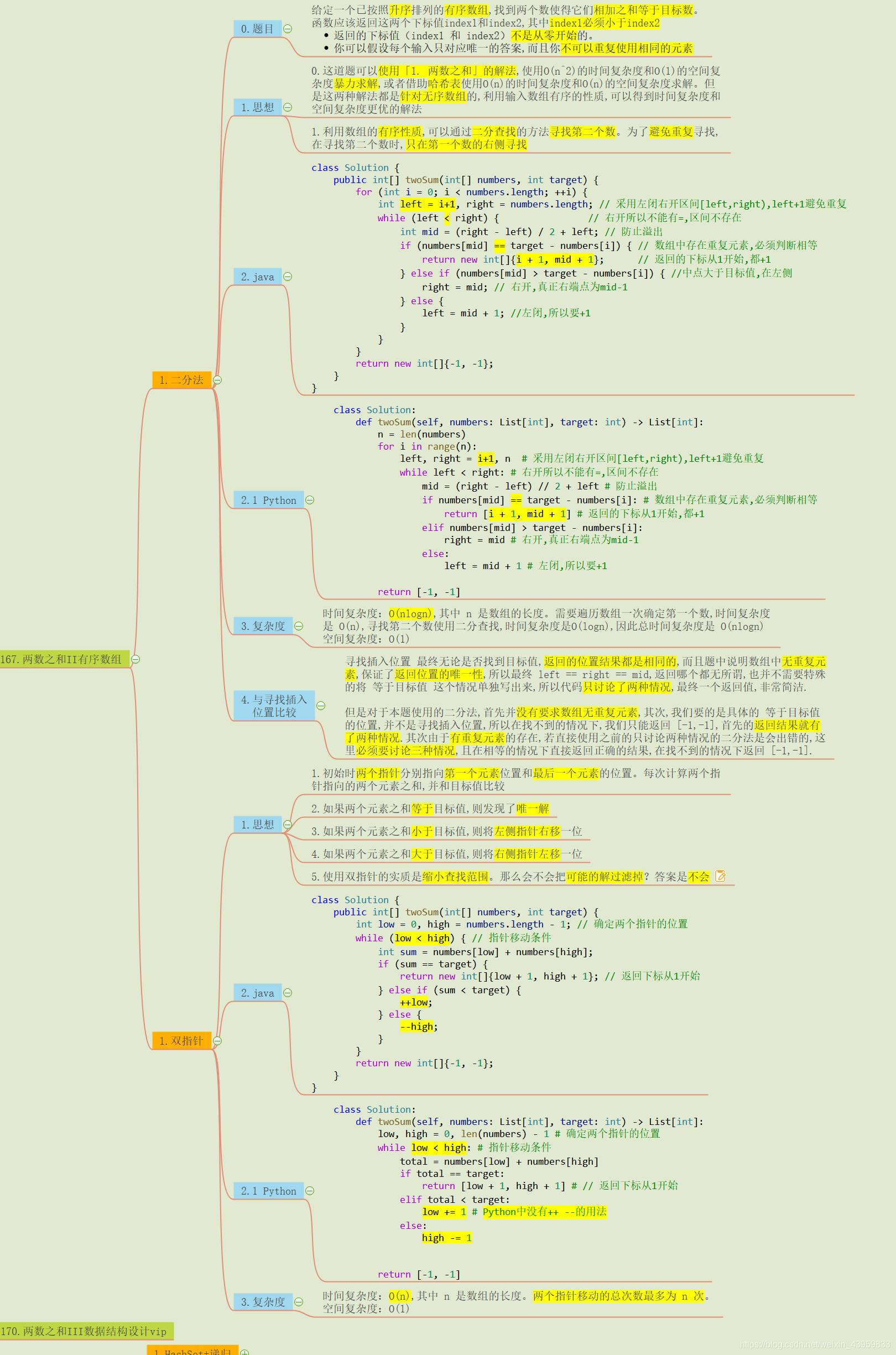
1.两数之和中有序和无序的区别

之前写了一篇关于无序数组的两数之和问题, 在无序数组中寻找第二个数就没有多少捷径, 毕竟数组无序, 很多经典的方法都用不上, 最后只能牺牲空间来换取时间, 利用哈希表将空间复杂度增加到了O(n), 从而降低了寻找第二个数的时间复杂度.

但是当数组有序之后, 就能使用一些经典的算法同时仍然保证空间复杂度为O(1), 不需要牺牲空间来换取时间, 比如下面马上介绍的 二分法 和 双指针 方法.

这里给我们提供了一种思维, 那我们是不是也可以将无序数组先进行排序后, 再使用这些经典算法呢? 当然可以这么做, 但对于两数之和来说, 必要性不是太大. 因为最快的排序算法也需要O(nlogn)的时间复杂度, 对于两数之和确实提升也不是太大, 但是对于 三数之和/四数之和 还是挺实用的, 后续文章将很快讲到.

2.二分法和寻找插入位置的区别

数组有序了, 使用二分法寻找第二个数就可以将时间复杂度降到O(logn)了, 关于二分法, 之前的这篇文章已经讲解的很清楚了, 这里就不再重复介绍了.

这里说说 二分法 和 寻找插入位置的不同, 也是两篇文章中代码不同的部分.

寻找插入位置 最终无论是否找到目标值, 返回的位置结果都是相同的, 而且题中说明数组中无重复元素, 保证了返回位置的唯一性, 所以最终 left == right == mid, 返回哪个都无所谓, 也并不需要特殊的将 等于目标值 这个情况单独写出来, 所以代码只讨论了两种情况, 最终一个返回值, 非常简洁.

但是对于本题使用的二分法, 首先并没有要求数组无重复元素, 其次, 我们要的是具体的 等于目标值 的位置, 并不是寻找插入位置, 所以在找不到的情况下, 我们只能返回 [-1, -1], 首先的返回结果就有了两种情况.

其次由于有重复元素的存在, 若直接使用之前的只讨论两种情况的二分法是会出错的, 这里必须要讨论三种情况, 且在相等的情况下直接返回正确的结果, 在找不到的情况下返回 [-1, -1].

本题另外的一个小的注意点是: 返回的下标从1开始, 只要在原本的返回结果上+1就可以了.

还有一个注意点是, 为了避免重复寻找,在寻找第二个数时,只在第一个数的右侧寻找, 也就是left = i+1.

3.双指针思想

双指针在有序数组中是非常重要的思想, 一定要掌握. 思想还是挺简单的, 但是优化的效果是非常棒的, 比二分法更加优秀. 导图中对思想的描述挺清楚了, 这里说下它的适用范围吧.

最基本最首要的前提是 数组一定要是有序的, 其次, 一定要涉及到几个数之间的相互关系, 最常用的也就是几个数相加等于某一定值的情况, 其他情况, 今后遇到了再细说. 常用于数组和链表之中.

源码

Python:

# 二分法
class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        n = len(numbers)
        for i in range(n):
            left, right = i+1, n  # 采用左闭右开区间[left,right),left+1避免重复
            while left < right: # 右开所以不能有=,区间不存在
                mid = (right - left) // 2 + left # 防止溢出
                if numbers[mid] == target - numbers[i]: # 数组中存在重复元素,必须判断相等
                    return [i + 1, mid + 1] # 返回的下标从1开始,都+1
                elif numbers[mid] > target - numbers[i]:
                    right = mid # 右开,真正右端点为mid-1
                else:
                    left = mid + 1 # 左闭,所以要+1
        
        return [-1, -1]

# 双指针
class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        low, high = 0, len(numbers) - 1 # 确定两个指针的位置
        while low < high: # 指针移动条件
            total = numbers[low] + numbers[high]
            if total == target:
                return [low + 1, high + 1] # // 返回下标从1开始
            elif total < target:
                low += 1 # Python中没有++ --的用法
            else:
                high -= 1


        return [-1, -1]

​

java:

// 二分法
class Solution {
    public int[] twoSum(int[] numbers, int target) {
        for (int i = 0; i < numbers.length; ++i) {
            int left = i+1, right = numbers.length; // 采用左闭右开区间[left,right),left+1避免重复
            while (left < right) {                // 右开所以不能有=,区间不存在
                int mid = (right - left) / 2 + left; // 防止溢出
                if (numbers[mid] == target - numbers[i]) { // 数组中存在重复元素,必须判断相等
                    return new int[]{i + 1, mid + 1};      // 返回的下标从1开始,都+1
                } else if (numbers[mid] > target - numbers[i]) { //中点大于目标值,在左侧
                    right = mid; // 右开,真正右端点为mid-1
                } else {
                    left = mid + 1; //左闭,所以要+1
                }
            }
        }
        return new int[]{-1, -1};
    }
}

// 双指针
class Solution {
    public int[] twoSum(int[] numbers, int target) {
        int low = 0, high = numbers.length - 1; // 确定两个指针的位置
        while (low < high) { // 指针移动条件
            int sum = numbers[low] + numbers[high];
            if (sum == target) {
                return new int[]{low + 1, high + 1}; // 返回下标从1开始
            } else if (sum < target) {
                ++low;
            } else {
                --high;
            }
        }
        return new int[]{-1, -1};
    }
}

​

三.三数之和 相比于 两数之和 的难点, 力扣15详细注解

题目链接: https://leetcode-cn.com/problems/3sum/

0.导图整理

1.对于不重复三元组的处理

本题最大的难点在于题目要求的 不重复的三元组, 三数之和 不像 两数之和 那样简单, 它的可重复情况是非常多的, 无法像 两数之和 那样, 只要将第一个元素放入哈希表中, 就可以轻松解决元素重复的问题了.

对于三数之和, 即使使用哈希表去重, 它的操作也是比较困难的. 所以我们不能简单地使用三重循环枚举所有的三元组, 然后使用哈希表进行去重操作, 这样的工作量比较大.

因此我们必须换一种方法来解决此题, 从源头上解决元素重复的问题. 如果给定的数组是有序的, 那么其中可重复的情况就是完全可以控制的了, 处理起来也是很简单的. 所以我们首先将数组中的元素从小到大进行排序, 随后使用普通的三重循环就可以满足上面的要求.

我们会发现其中重复的元组都是相邻的元组, 只需要保证在每一重循环时, 相邻两次枚举的元素不是相同的元素, 这样就可以避免元组重复的情况了. 也就是导图中每层循环时的 if判断语句.

2.双指针的思想

使用普通的三层循环确实也能解决问题, 但是O(n^3)的时间复杂度也确实太高了, 这时我们想到了在 有序数组的两数之和 中使用的双指针的方式(双指针在此文已说明清楚, 这里就不重复讲解了), 虽然现在是三数之和, 但当我们正常遍历了第一层循环之后, 剩下的两个数不就形成了 有序数组的两数之和 了吗? 所以我们只要 保持第二重循环不变, 而将第三重循环变成一个从数组最右端开始向左移动的指针, 同时加上上述讨论的避免重复的条件, 最终代码就完成了.

时间复杂度也从O(n^3) 降到了 O(n^2), 至于空间复杂度, 有两种情况: 如果允许我们改变原来的数组, 那么只需要排序算法额外的空间复杂度O(logN), 如果不允许的话, 那就要使用了一个额外的数组存储了nums的副本并进行排序,空间复杂度为 O(N).

3.元素为整型链表的数组链表: ArrayList<List>()

这里补充说明下这个数据结构, 对于新手来说, 看着还是挺吓人的呢! 我们从外到里依次来拆分这个结构. 首先最外面 ArrayList() 表明它的本质是一个数组链表, 无论里面的元素是什么类型, 它最本质的结构都不会发生变化的. 再来看它里面所装的结构是 List, 就是说这个数组链表中的每一个元素都是一个链表List, 长度可以是任意的长度, 但是这个链表List中的元素的类型必须是整型Integer. 这里的<>用到了java中的 泛型 的概念, 简单来说就是一个写一个通用的模板, 里面所包含元素的类型可以是任意的, 具体使用时对其指定具体的类型即可. 对于较复杂的数据类型, 一般都是采用这种由外到内的分析方法.

对应本题来说下具体的应用: ans.add(Arrays.asList(nums[first],nums[second],nums[third])), 首先ans这个数组链表使用.add函数添加了一个链表, 而这个链表是通过 3个整型数据 由Arrays.asList()这个方法转换成的链表, 这样就成功添加了一个链表. 之后每次循环, 只要有满足条件的三元组都会添加一个链表, 最终所有满足条件的三元组链表形成了最终结果的数组链表ans.

对于java和C++这种强类型的语言, 使用时要明确指明所用到的数据类型, 但对于Python这种弱类型的语言来说, 用起来就非常简单了, 你只需要创建了链表list(), 不需要指明任何类型, 使用时直接添加某种特定类型的数据即可. 而且每次添加的数据会自动保存为一个链表的形式添加到链表中, 不需要显式地自己将其转化为链表, 用起来还是很简单的.

源码

Python:

​
class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]: # 元素为整型链表的数组链表
        n = len(nums)
        nums.sort()   # 将数组进行排序
        ans = list()
        
        # 枚举 a
        for first in range(n):
            # 需要和上一次枚举的数不相同
            if first > 0 and nums[first] == nums[first - 1]:
                continue
            # c 对应的指针初始指向数组的最右端
            third = n - 1
            target = -nums[first]
            # 枚举 b
            for second in range(first + 1, n):
                # 需要和上一次枚举的数不相同
                if second > first + 1 and nums[second] == nums[second - 1]:
                    continue
                # 需要保证 b 的指针在 c 的指针的左侧
                while second < third and nums[second] + nums[third] > target:
                    third -= 1
                if second == third: # 如果指针重合,后续也不会满足条件,可以退出循环
                    break
                if nums[second] + nums[third] == target:
                    ans.append([nums[first], nums[second], nums[third]])
        
        return ans

​

java:

​
class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        int n = nums.length;
        Arrays.sort(nums); //将数组进行排序
        List<List<Integer>> ans = new ArrayList<List<Integer>>(); //元素为整型链表的数组链表
        // 枚举 a
        for (int first = 0; first < n; ++first) {
            // 需要和上一次枚举的数不相同
            if (first > 0 && nums[first] == nums[first - 1]) {
                continue;
            }
            // c 对应的指针初始指向数组的最右端
            int third = n - 1;
            int target = -nums[first];
            // 枚举 b
            for (int second = first + 1; second < n; ++second) {
                // 需要和上一次枚举的数不相同
                if (second > first + 1 && nums[second] == nums[second - 1]) {
                    continue;
                }
                // 需要保证 b 的指针在 c 的指针的左侧
                while (second < third && nums[second] + nums[third] > target) {
                    --third;
                }
                if (second == third) { // 如果指针重合,后续也不会满足条件,可以退出循环
                    break;
                }
                if (nums[second] + nums[third] == target) {
                    ans.add(Arrays.asList(nums[first],nums❤️思维导图整理大厂面试高频数组12: 4种方法彻底解决接雨水问题, 力扣42❤️


 ❤️思维导图整理大厂面试高频数组12: 4种方法彻底解决接雨水问题, 力扣42❤️


 ❤️思维导图整理大厂面试高频数组10: 3种方法彻底解决中位数问题, 力扣4❤️


 ❤️思维导图整理大厂面试高频数组9: 删除重复元素的通解问题, 力扣26/80❤️


 ❤️思维导图整理大厂面试高频数组10: 3种方法彻底解决中位数问题, 力扣4❤️


 ❤️思维导图整理大厂面试高频数组16: 最长湍流子数组的动态规划构建 和 滑动窗口解法, 力扣978❤️