数据结构二叉树链式结构的实现

Posted 2021-09-26 Huang_ZhenSheng

目录

二叉树的遍历：

前序遍历递归图解： 

​

二叉树的链式结构的实现：

二叉树的节点个数：

二叉树的节点个数方法1：

二叉树的节点个数方法2：

二叉树的节点个数方法3：

二叉树叶子节点个数：

二叉树第k层节点的个数 :

二叉树的深度/高度: 

二叉树查找值为x的节点: 

---

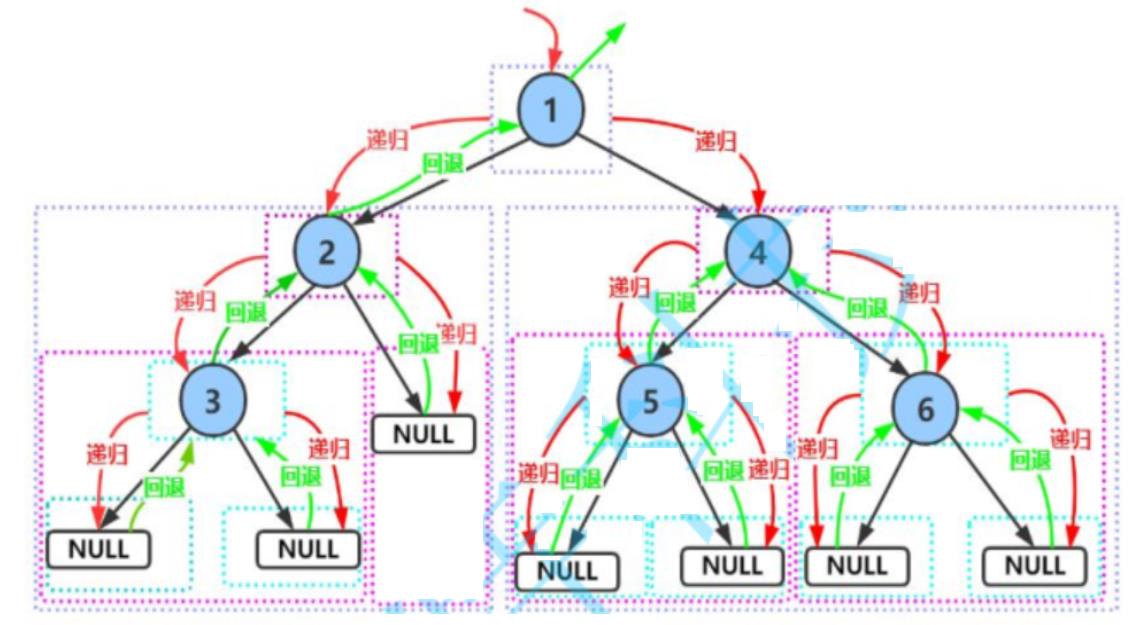
二叉树的遍历：

所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。

按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：

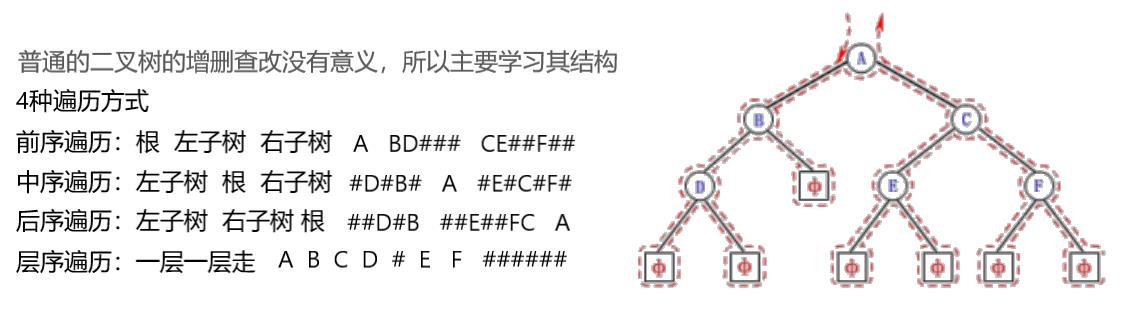
前序遍历递归图解： 

详细图解： 

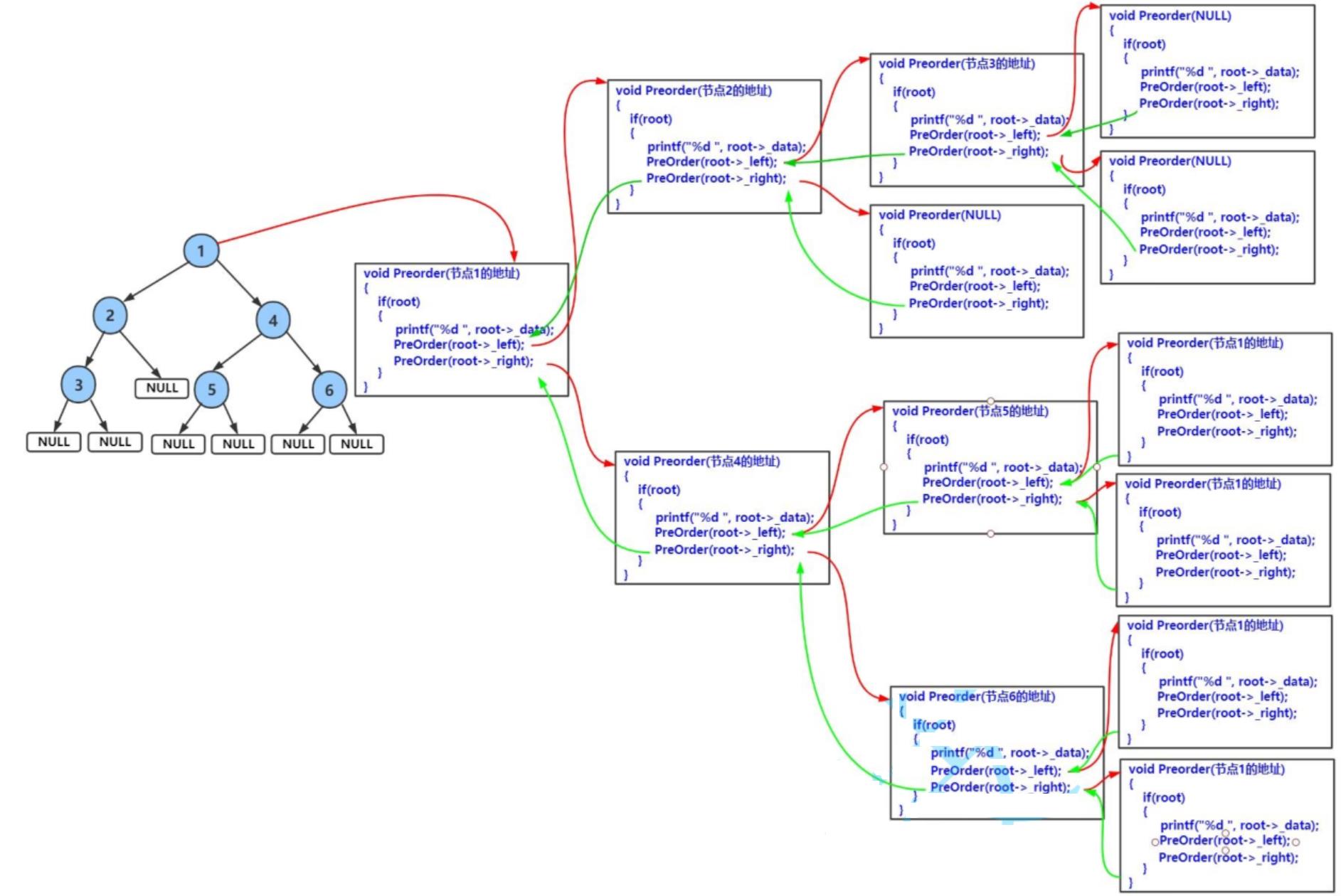
简单图解： 

二叉树的链式结构的实现：

主要包含：（注重递归的理解）

二叉树节点个数

二叉树叶子节点个数

二叉树第K层节点个数

二叉树深度/高度

二叉树查找值为X的节点

二叉树的节点个数：

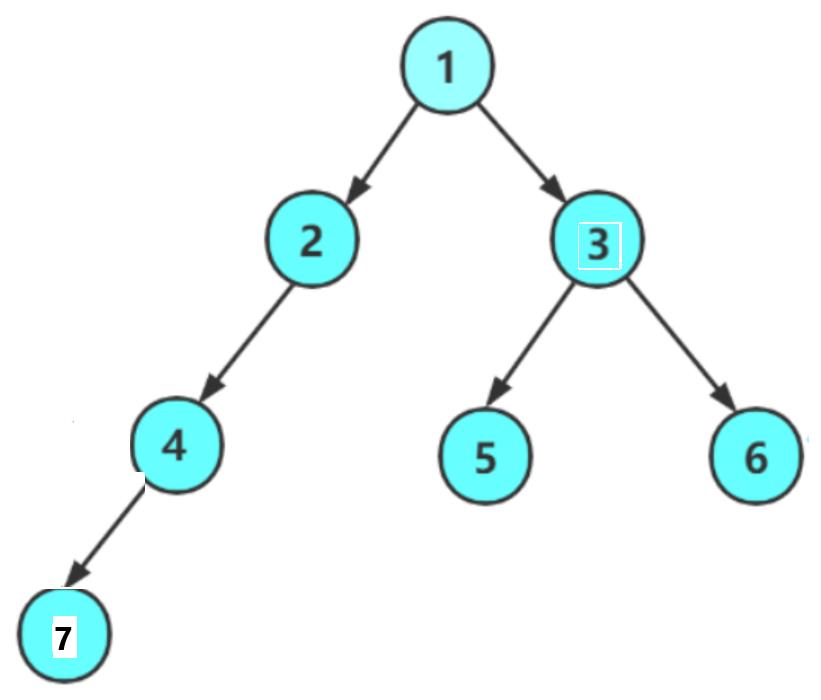
这里先创建一个二叉树：

typedef char BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

BTNode* BuyNode(BTDataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	node->data = x;
	node->left = NULL;
	node->right = NULL;
	return node;
}
BTNode* CreatBinaryTree()
{
	BTNode*node1 = BuyNode('A');
	BTNode*node2 = BuyNode('B');
	BTNode*node3 = BuyNode('C');
	BTNode*node4 = BuyNode('D');
	BTNode*node5 = BuyNode('E');
	BTNode*node6 = BuyNode('F');
	BTNode*node7 = BuyNode('G');

	node1->left = node2;
	node1->right = node3;
	node2->left = node4;
	node3->right = node5;
	node3->left = node6;
	node4->left = node7;
	return node1;
}

int main()
{
	BTNode* root = CreatBinaryTree();
	printf("BinaryTreeSize:%d",BinaryTreeSize(root));
	return 0;
}

二叉树的节点个数方法1：

遍历：全局变量

//遍历：全局变量
int size = 0;
void BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	else
	{
		size++;
	}
	BinaryTreeSize(root->left);
	BinaryTreeSize(root->right);
}

二叉树的节点个数方法2：

遍历：局部变量

//遍历：局部变量
void BinaryTreeSize(BTNode* root,int* psize)
{
	if (root == NULL)
	{
		return;
	}
	else
	{
		(*psize)++;
	}
	BinaryTreeSize(root->left,psize);
	BinaryTreeSize(root->right,psize);
}

二叉树的节点个数方法3：

分治思想：

先遍历左子树，在遍历右子树，然后在加根节点1

//分治
int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	else
	{
		return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
	}
}

二叉树叶子节点个数：

如果节点的左孩子跟右孩子都为空，则+1

//二叉树叶子节点的个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	else if(root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	else
	{
		return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
	}
}

二叉树第k层节点的个数 :

//二叉树第k层节点的个数
int BinaryTreeLevelkSize(BTNode* root,int k)
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	else
	{
		return  BinaryTreeLevelkSize(root->left, k-1) + BinaryTreeLevelkSize(root->right, k-1);
	}

}

二叉树的深度/高度: 

//二叉树的深度/高度
int BinaryTreeDepth(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int leftleaf = BinaryTreeDepth(root->left);
	int leftright = BinaryTreeDepth(root->right);
	return leftleaf > leftright? leftleaf+1 : leftright+1;
}

二叉树查找值为x的节点: 

//二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}
	BTNode* retleft = BinaryTreeFind(root->left,x);
	if (retleft)
	{
		return retleft;
	}
	BTNode* retright = BinaryTreeFind(root->right, x);
	if (retright)
	{
		return  retright;
	}
	return NULL;
}