频域分析频谱泄露频率分辨率栅栏效应
Posted Zhi Zhao
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了频域分析频谱泄露频率分辨率栅栏效应相关的知识，希望对你有一定的参考价值。
信号的频域分析
一、时域加窗
现实生活中的信号大部分是连续的，通过对连续的信号进行采样得到散时间信号，但是计算机所能处理的数据都是有限长的，因而我们可以对原始序列做加窗处理使其成为有限长序列。
以矩形窗为例，其时域表达式为：
式(1)中，
N
=
M
+
1
N=M+1
N=M+1，为矩形窗的长度。
对无限长序列进行加窗处理，就是对序列在时域上乘以一个窗函数。
由卷积定理可以得到，时域的相乘等于频域的卷积。
设仿真信号的时域表达式为：
x
(
t
)
=
A
0
∗
c
o
s
(
2
π
f
0
t
)
+
A
1
∗
c
o
s
(
2
π
f
1
t
)
x(t)=A_{0}*cos(2πf_{0}t)+A_{1}*cos(2πf_{1}t)
x(t)=A0∗cos(2πf0t)+A1∗cos(2πf1t)
x
(
t
)
x(t)
x(t)做傅里叶变换（FT）的频域表达式为：
X
(
j
Ω
)
=
A
0
π
δ
(
Ω
+
Ω
0
)
+
A
0
π
δ
(
Ω
−
Ω
0
)
+
A
1
π
δ
(
Ω
+
Ω
0
)
+
A
1
π
δ
(
Ω
−
Ω
0
)
X(jΩ)=A_{0}πδ(Ω+Ω_{0})+A_{0}πδ(Ω-Ω_{0})+A_{1}πδ(Ω+Ω_{0})+A_{1}πδ(Ω-Ω_{0})
X(jΩ)=A0πδ(Ω+Ω0)+A0πδ(Ω−Ω0)+A1πδ(Ω+Ω0)+A1πδ(Ω−Ω0)
连续信号
x
(
t
)
x(t)
x(t)的波形及频谱如图1所示。
连续信号
x
(
t
)
x(t)
x(t)经过采样后，得到的离散时间的表达式为：
x
[
n
]
=
x
(
t
)
∣
t
=
n
T
s
x[n]=x(t)|_{t=nT_{s}}
x[n]=x(t)∣t=nTs
离散序列
x
[
n
]
x[n]
x[n]做离散时间傅里叶变换（DTFT）的频域表达式为：
X
(
e
j
w
)
=
1
T
s
∑
k
=
−
∞
∞
X
(
j
w
T
s
−
j
k
2
π
T
s
)
X(e^{jw})=\\frac{1}{T_{s}}\\sum_{k=-∞}^{∞}X(j\\frac{w}{T_{s}}-jk\\frac{2π}{T_{s}})
X(ejw)=Ts1k=−∞∑∞X(jTsw−jkTs2π)
离散序列
x
[
n
]
x[n]
x[n]的波形及频谱如图2所示。
矩形窗函数
w
[
n
]
w[n]
w[n]做离散时间傅里叶变换（DTFT）的频域表达式为：
W
(
e
j
w
)
=
e
−
j
w
(
N
−
1
)
/
2
∗
s
i
n
(
w
N
/
2
)
s
i
n
(
w
/
2
)
W(e^{jw})=e^{-jw(N-1)/2} *\\frac{sin(wN/2)}{sin(w/2)}
W(ejw)=e−jw(N−1)/2∗sin(w/2)sin(wN/2)
矩形窗函数
w
[
n
]
w[n]
w[n]的波形及频谱如图3所示。
离散序列
x
[
n
]
x[n]
x[n]与窗函数
w
[
n
]
w[n]
w[n]的卷积为：
V
(
e
j
w
)
=
1
2
π
∫
−
π
π
X
(
e
j
θ
)
W
(
e
j
(
w
−
θ
)
)
d
θ
=
A
0
2
W
(
e
j
(
w
+
w
0
)
)
+
A
0
2
W
(
e
j
(
w
−
w
0
)
)
+
A
1
2
W
(
e
j
(
w
+
w
0
)
)
+
A
1
2
W
(
e
j
(
w
−
w
0
)
)
V(e^{jw})=\\frac{1}{2π}\\int_{-π}^{π}X(e^{jθ})W(e^{j(w-θ)})dθ=\\frac{A_{0}}{2}W(e^{j(w+w_{0})})+\\frac{A_{0}}{2}W(e^{j(w-w_{0})})+\\frac{A_{1}}{2}W(e^{j(w+w_{0})})+\\frac{A_{1}}{2}W(e^{j(w-w_{0})})
V(ejw)=2π1∫−ππX(ejθ)W(ej(w−θ))dθ=2A0W(ej(w+w0))+2A0W(ej(w−w0))+2A1W(ej(w+w0))+2A1W(ej(w−w0))
截断后的离散序列
v
[
n
]
v[n]
v[n]的波形及频谱如图4所示。
频谱泄露
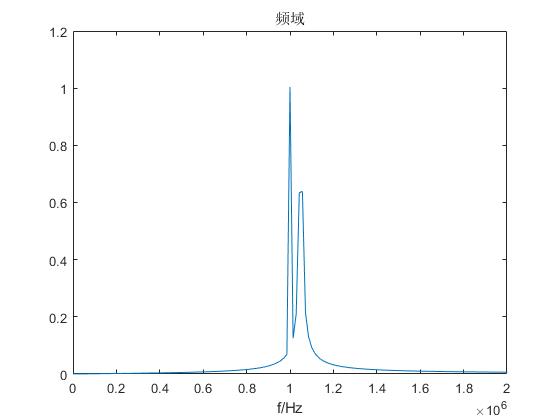
信号的频率成分包括1MHz和1.05MHz，1MHz对应的幅值为1，但是1.05MHz的幅值减小了，且在其他频率点上都有不小的幅值。这就是出现了频谱泄露的现象。
产生频谱泄露的原因是什么？
由于计算机只能处理有限长的数据，所以需要对采集的信号进行截断，相当于对原始信号做了加窗处理。对信号加窗就是对信号在时域上乘以一个窗函数，时域的乘积对应频域的卷积，而窗函数的频域包括主瓣和旁瓣，旁瓣造成了信号频谱的泄漏。频域泄漏不可避免，只能减小。
如何抑制这一现象？
可以取更长的数据点
以上是关于频域分析频谱泄露频率分辨率栅栏效应的主要内容，如果未能解决你的问题，请参考以下文章
从Matlab平台进行FFT到ARM平台C语言FFT频谱分析
数字信号处理 频域采样及恢复（离散频谱到连续频谱） MATLAB