2021数学建模国赛C题思路 生产企业原材料的订购与运输 第一版思路 思路开源 已修订 程序

Posted 2021-09-25 您好啊数模君

原创开源思路下载链接，程序已出，怕大家不会用程序，下面链接中加了一般能跑通的程序

链接：https://pan.baidu.com/s/13aSy2-hlkLa7Ps8wknYY1Q 
提取码：gap4

这里有百种算法出处整理，本题算法可从上面找取：

给裸赛的家人们整理了百种算法出处https://mp.weixin.qq.com/s/OhWRCeep885MuyhMhvdiOw

 这道题是优化问题，先看看题目，以下为题目告知的条件和目标函数

条件：

①生产48周，每周产能2.82wm³，折合每周需要A类原材料1.692wm³或B原材料1.8612wm³或C原材料2.0304wm³；

②24周的原材料订购和转运计划，那么相当于平均每周需要送达的材料能够满足5.64wm³，这里是包含了订购及转运时间加起来共计24周以内要完成，如果考虑8家转运商满负荷运转以及平均损耗，那么一天送达的就有4.75wm³,就算是按最低的材料置换产能的比例也能大于5.64wm³，所以运输这块没啥问题，接下来看供应商供应能力，如果也按取平均，那么肯定是不够的，所以可以取最大供应量的周数据作为该供应商最大供应能力的体现

③A类和B类原材料的采购单价分别比C类原材料高20%和10%，那么就假设C单位立方米成本为1，A成本为1.2，B成本为1.1；

④三类原材料运输和储存的单位费用相同，一般运输一批货物只算单次运输的费用，这里的储存费用就不用按照每周多少来考虑，如果要考虑，那么就要涉及到储存的材料使用情况，毕竟边供应边生产；

⑤我们可以就假设当周订货当周送达

目标函数：

一家供应商每周供应的原材料尽量由一家转运商运输，也就是说供应商数要少，供应商数可作为一目标函数

接下来看问题

第一问确定50家最重要的供应商，一般的都是从供应情况去看，这里可以确定一些指标，然后进行评价，最后评分最高Top50作为本问结果，可以考虑以下指标：

①供应商都是只供应一种原料，那么就会有材料得性价比，算一下哪一个原材料经济效益最高，用1/[0.6 0.66 0.72]=[1.67 1.52 1.39]，然后再去除下单价/[1.2 1.1 1]=[1.3889 1.3774 1.3889]，然后各供应商按供应的原材料对应，将这个结果作为第一个指标，指标越大越好

②供应商最大供应能力，最大供应量并换算为产能，指标越大越好

③供应商平均供应能力，平均供应量并换算为产能，指标越大越好

④供应商供应得稳定性，对历史供应数据，做下方差，指标越小越好

⑤历史供应量/历史订单量比，指标越大越好

。。。

除了以上指标大家还可以多增加一些，然后用评价算法评价后排序即可，第一问评价可以用多种算法例如投影寻踪、熵权法、Tosis等评价，然后在通过组合评价方法例如Borda求一个综合性的评价值，然后进行排序，但是注意这里对数据进行标准化时有一个问题，客观算法可能会存在偏离主观的现象，可以这么来做，对于你们认为的重要性小的指标可以通过ln(β+x)函数映射，这样能够减少该指标对最后结果的影响

第二问，A、C类原材料经济效益最高，我们发现C类原材料运输费用和储存费用要比AB较高，因为置换为产能需要更多的供应量，并且供应C类材料的供应商是最少的，在本问，考虑供应商的最大供应能力即可，但是为了方便运算，最好是再增加一个产能计算，最大供应能力就以历史5年中供应量最大的一周作为起最大供应能力，对于转运商的运输损耗，可以直接取平均，也可以预测未来24周的每周的损耗都可以，前者更简单，对于本问建模部分，采用优化算法进行多目标求解，目标函数有：1、供应商数最少，2、总成本=运输成本+储存成本=2*运输成本最低；约束条件有：1、24周从供应到转运结束的原材料转化为产能要达标，2、只有24周转运时间，3、每周至多送达8*6000*损耗，4、每周至多订购8*6000的供货量。为了降低寻优维度，可以增加这样一个优先条件，C原材料置换为产能置换率最低，那么C原材料就优先用损耗较大转运商转运，这样对整体的产能损耗较小，其次为B

第二问设计启发式算法如下：

第三问，尽量多地采购 A 类和尽量少地采购 C 类原材料，以减少转运及仓储的成本，同时希望转运商的转运损耗率尽量少，本问在第二问基础上增加一个目标函数A类原材料-C材料采购量为目标函数，同样按第二问方法来做

第四问，只考虑产能，转运商运能拉满情况下去选择供应商，每周最多订6000m³*8=4.8wm³，考虑所有Top50供应商日均ABC类最大供应量，在第二问基础上，第四问增加一个目标函数为产能的最大化，同样按第二问做法来做，但题目说的很明确了，A类材料才是最合适的材料，但是第二问算法中涉及到k个供应商的选取，那么第四问实则就只是选择最佳供应商而已，对于供应量，按A、B、C类原材料的供应商依次按最大供应量选取，直到供应量达到4.8wm³为止，对于选择转运商还是按第二问默认的规则来，C类材料给损耗率最大的转运商

本题目优与供应商数会发生变化，建议通过模拟退火算法框架进行寻优

第一问结果决定后面问效果，方法慎选

评价方法自己选

指标提取

clear X1=xlsread('附件1 近5年402家供应商的相关数据.xlsx','企业的订货量（m?）'); X2=xlsread('附件1 近5年402家供应商的相关数据.xlsx','供应商的供货量（m?）'); [~,X3,~]=xlsread('附件1 近5年402家供应商的相关数据.xlsx','企业的订货量（m?）'); X3=string(X3); X3=X3(2:end,2); X3(find(X3=="A"))=1.3889; X3(find(X3=="B"))=1.3774; X3(find(X3=="C"))=1.3889; %从供应角度看供应商的供应情况 Y(:,1)=max(X2')';%供应商最大供应能力，正向指标 Y(:,2)=mean(X2,2);%供应商平均供应能力，正向指标 Y(:,3)=1./std(X2')';%供应商供应的稳定性,对历史供应数据，做方差，负向指标，可以做个倒数 Y(:,4)=double(X3);%供应商材料经济效益，正向指标 Y(:,5)=sum(X2,2)./sum(X1,2);%历史供应量/历史订单量比，正向指标 %从企业角度看对供应商的认可情况 Y(:,6)=max(X1')';%供应商最大订单量，正向指标 Y(:,7)=mean(X1,2);%供应商平均订单量，正向指标 Y(:,8)=1./std(X1')';%供应商订单量的稳定性,对历史供应数据，做方差，负向指标，可以做个倒数 %还有其他指标可自加 Y=log(1+Y);%对指标ln函数映射，以减少数据本身差距，将评分重心转移至权重 Y=mapminmax(Y',0,1)';

层次分析评价

a=[1 5/4 5/4 5/9 5/8 5/6 1 1     4/5 1 1 4/9 4/8 4/6 4/5 4/5     4/5 1 1 4/9 4/8 4/6 4/5 4/5     9/5 9/4 9/4 1 9/8 9/6 9/5 9/5     8/5 2 2 8/9 1 8/6 8/5 8/5     6/5 6/4 6/4 6/9 6/8 1 6/5 6/5     1 5/4 5/4 5/9 5/8 5/6 1 1     1 5/4 5/4 5/9 5/8 5/6 1 1];  %构建判断矩阵 n1=length(a); %a矩阵的长度 [x,y]=eig(a); %求特征值 lamda=max(diag(y)) %最大特征向量 num=find(diag(y)==lamda); w0=x(:,num)/sum(x(:,num)) %准则层权向量 ri=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45]; %平均随机一致性指标 CR1=(lamda-n1)/(n1-1); %一致性指标 CR=CR1/ri(n1); %一致性比例 if CR>=0.10     disp('矩阵没通过一致性检验，请重新调整矩阵'); else     disp('矩阵通过一致性检验'); end f=Y*w0; [f,paixu]=sort(f,'descend');

熵权法评价

[n,m]=size(Y); for i=1:n     for j=1:m         p(i,j)=Y(i,j)/sum(Y(:,j));     end end %% 计算第 j 个指标的熵值 e(j) k=1/log(n); for j=1:m     e(j)=-k*sum(p(:,j).*log(p(:,j))); end d=ones(1,m)-e; % 计算信息熵冗余度 w=d./sum(d) % 求权值 w f=Y*w'; [f,paixu]=sort(f,'descend');

秩和比

w=[0.0532   0.3138  0.0865  0.0000  0.1076  0.0318  0.1549  0.2523];%通过其他方法求得的权重 ra=tiedrank(Y); [n,m]=size(ra);%求矩阵维度 RSR=mean(ra,2)/n; W=repmat(w,[n,1]);%用于复制平铺矩阵，相当于讲w矩阵看成一个元素，形成n×1维的矩阵并用W矩阵记录 WRSR=sum(ra.*W,2)/n;%加权秩和比 [sWRSR,ind]=sort(WRSR,'descend');%sort为排序函数 p=[1:n]/n; p(end)=0.99999; Probit=norminv(p,0,1); X=[ones(n,1),Probit']; [ab,abint,r,rint,stats]=regress(sWRSR,X); WRSRfit=ab(1)+ab(2)*Probit; f=WRSRfit'; paixu=ind;

Topsis

[n,m]=size(Y); %n为A矩阵的行数，m为A矩阵的列数 c=sqrt(sum(Y.*Y)); %规范化决策矩阵 d=Y./c; w=[0.0532   0.3138  0.0865  0.0000  0.1076  0.0318  0.1549  0.2523];%通过其他方法求得的权重 c=w.*d; cmax=max(c); cmin=min(c); for i=1:n     c1=c(i,:)-cmax;     s1(i)=norm(c1);     c2=c(i,:)-cmin;     s2(i)=norm(c2);     T(i)=s2(i)/(s1(i)+s2(i)); end %排名 [~,pm]=sort(T,'descend'); disp('评分结果，评分区间[0,1]') disp(T) disp('方案排名') disp(pm)

因子分析

X=Y; mapping.mean = mean(X, 1); X = X - repmat(mapping.mean, [size(X, 1) 1]);%去均值 C = cov(X);%协方差矩阵 C(isnan(C)) = 0; C(isinf(C)) = 0; [M, lambda] = eig(C);%求C矩阵特征向量及特征值 [lambda, ind] = sort(diag(lambda), 'descend');%排序 lambda=lambda./sum(lambda); L=lambda; lambda=cumsum(lambda); mapping.lambda = lambda; k=find(lambda>0.95); M = M(:,ind(1:k(1)));%%取前k列 mappedX = X * M;%降维后的X mappedX=mapminmax(mappedX',0,1)'; L=L(1:k(1))./sum(L(1:k(1)));%贡献率归一化 f=mappedX*L; [f,paixu]=sort(f,'descend');

投影寻踪-聪明的鲨鱼(自己改名)

w1=[0.0532   0.3138  0.0865  0.0000  0.1076  0.0318  0.1549  0.2523];%通过其他方法求得的权重 [bestx,f]=youhua(w1,Y);

function [bestx,f1]=youhua(w1,p) %% 启发式算法+投影寻踪 %可调参数 sub=w1.*0.5; %自变量下限 up=w1.*1.5; %自变量上限 opt=1;%-1为最小化，1为最大化 % 程序为最小化寻优，如果是最大化寻优更改排序部分程序即可 n=length(sub); %自变量个数 num=100*n^2; %种群大小 if num>10000     num=10000; end det=10+10*n;%迭代次数 k=1.5+0.1*n;%k为最大环绕圈数 R=0.01*n;%当鲨鱼进入猎物该范围，则直接对猎物位置进行逼近 Mc=(up-sub).*0.1;%猎物行动最大范围 x=[]; f=[]; for i=1:num     x(i,:)=sub+(up-sub).*rand(1,n); %初始化位置     f(i,1)=Target(p,x); end %以最小化为例 if opt==-1     [bestf,a]=min(f);%记录历史最优值     bestx=x(a,:);%记录历史最优解 elseif opt==1     [bestf,a]=max(f);%记录历史最优值     bestx=x(a,:);%记录历史最优解 end trace=[]; trace(1)=bestf; xx=[];ff=[]; for ii=1:det     %猎物躲避,蒙特卡洛模拟周围1000次，并选择最佳的点作为下一逃跑点     d=[];     d=pdist2(bestx,x);     d=sort(d);     z=exp(-d(2)/mean(Mc));%猎物急躁系数     z=max(z,0.1);     dx=[];     yx=[];     bestt=[];     bestc=[];     for i=1:1000         m=[];         for k=1:n             m=[m,(-1)^randi([1,2])];         end         xd=[];         xd=bestx+Mc.*z.*((det-ii)/det).*rand(1,n).*m;         xd=max(sub,xd);         xd=min(up,xd);         dx=[dx;xd];%(det-ii)/det表示随着追捕，猎物可逃窜的范围越来越小         yx=[yx;Target(p,xd)];     end     if opt==-1         [bestt,a]=min(yx);%选择最佳逃跑点         bestc=dx(a,:);         if bestt<bestf             bestf=bestt;             bestx=bestc;         end     elseif opt==1         [bestt,a]=max(yx);%选择最佳逃跑点         bestc=dx(a,:);         if bestt>bestf             bestf=bestt;             bestx=bestc;         end     end     %鲸鱼追捕     for i=1:num         %更新公式         if sqrt(sum((x(i,:)-bestx).^2))<=R             xx(i,:)=x(i,:)+rand.*(x(i,:)-bestx);             xx(i,:)=max(sub,xx(i,:));             xx(i,:)=min(up,xx(i,:));             ff(i,1)=Target(p,xx(i,:));         else             xx(i,:)=x(i,:)+real(shayu(x(i,:)-bestx,k));             xx(i,:)=max(sub,xx(i,:));             xx(i,:)=min(up,xx(i,:));             ff(i,1)=Target(p,xx(i,:));         end     end     %引入上一代进行排序,并重新分配角色     F=[bestf;f;ff];     X=[bestx;x;xx];     if opt==-1         [F,b]=sort(F,'ascend');%按小到大排序     elseif opt==1         [F,b]=sort(F,'descend');%按大到大排序     end     X=X(b,:);     f=F(1:num,:);     x=X(1:num,:);     if opt==-1         [bestf,a]=min(f);%记录历史最优值     elseif opt==1         [bestf,a]=max(f);%记录历史最优值     end     bestx=x(a,:);%记录历史最优解     trace=[trace;bestf]; end bestx=bestx./sum(bestx); disp(["投影寻踪计算权重结果为：",string(bestx)]) f1=[p*bestx'];

function f=shayu(X,K) %X为鲸鱼坐标减去猎物坐标 %k为最大围绕圈数 n=length(X); Y=[]; y=[]; costheta=[]; theta=[]; k=[]; for i=1:n-1     Y=[X(1:i),0];     y(i)=sqrt(sum(X(1:i+1).^2));     %计算角度（圈数）     costheta(i)=(X(1:i+1)*Y')/(sqrt(sum(X(1:i+1).^2))*sqrt(sum(Y.^2)));     if isnan(costheta(i))==1         costheta(i)=1;     end     if X(i+1)>=0         theta(i)=acos(costheta(i))/(2*pi);     else         theta(i)=2-acos(costheta(i))/(2*pi);     end     theta(i)=theta(i)*2*pi;     %自适应调节k     if y(i)>=10         k(i)=K*exp(-2);     else         k(i)=K*exp(-y(i)/5);     end end %位置更新公式，左包围或右包围 f=[]; l=[]; yy=y; ttheta=theta; l=k(1).*rand; yy(1)=yy(1).*exp(-l); ttheta(1)=ttheta(1)+l*2*pi*(-1).^randi([1,2]); f=[yy(1).*cos(ttheta(1));yy(1).*sin(ttheta(1))]; if n>2     for j=1:n-2         a=mod(j,2);         if a==1             l=k(j+1).*rand;             yy(j+1)=yy(j+1).*exp(-l);             ttheta(j+1)=ttheta(j+1)+l*2*pi*(-1).^randi([1,2]);             f=[f.*abs(cos(ttheta(j+1)));yy(j+1).*sin(ttheta(j+1))];         elseif a==0             l=k(j+1).*rand;             yy(j+1)=yy(j+1).*exp(-l);             ttheta(j+1)=ttheta(j+1)+l*2*pi*(-1).^randi([1,2]);             f=[f.*abs(sin(ttheta(j+1)));yy(j+1).*cos(ttheta(j+1))];         end     end end f=f';

function y=Target(x,a) %计算目标函数值 m=[]; n=[]; [m,n]=size(x); z=[]; for i=1:m     s1=0;     for j=1:n         s1=s1+a(j)*x(i,j);     end     z(i)=s1; end Sz=[]; Sz=std(z);%方差 R=[]; R=0.1*Sz; s3=0; r=[]; t=[]; u=[]; for i=1:m     for j=1:m         r=abs(z(i)-z(j));         t=R-r;         if t>=0             u=1;         else             u=0;         end         s3=s3+t*u;     end end Dz=[]; Dz=s3; y=[]; y=Sz*Dz; end

组合评价模型—模糊Borda

组合评价模型—模糊Borda(Matlab)https://mp.weixin.qq.com/s/Y4UNRIuUjSMgHbE2oa2jkg

或者采用类似一下公式组合权重再进行评价

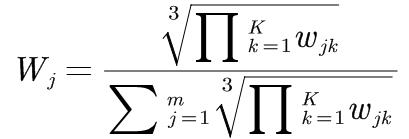
第二问程序

以模拟退火框架写的，可更改为其他优化算法，程序以发布的思路编写的，如有不懂请结合思路理解，程序仅为参考，切勿照搬

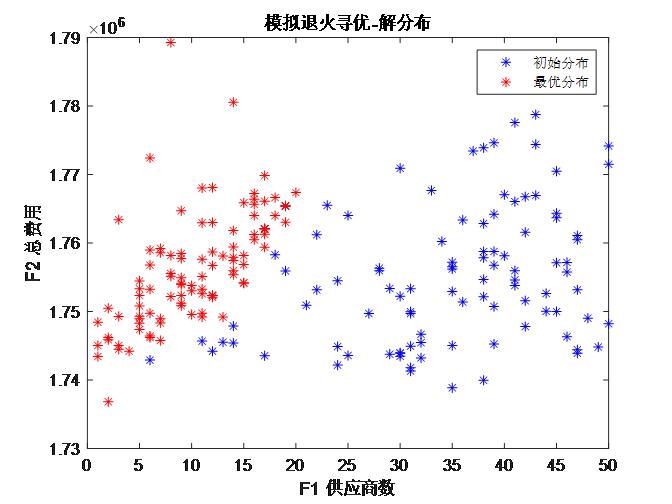
clear %% 第一部分请自行修改为第一问的Top50供应商 %直接运行程序十有八九会报错，因为是随机选的50，请将aa矩阵更改为你们第一问的结果Top50的编号 [~,X1,~]=xlsread('附件1 近5年402家供应商的相关数据.xlsx','企业的订货量（m?）'); X1=string(X1); X1=X1(2:end,2); X2=xlsread('附件1 近5年402家供应商的相关数据.xlsx','供应商的供货量（m?）'); X3=xlsread('附件2 近5年8家转运商的相关数据.xlsx'); X3=mean(X3,2);%这里我直接取平均损耗了 XXX3=X3; [X3,x3]=sort(X3); X3=[X3,6000.*ones(8,1)];%加上最大转运量，方便调用 Y=zeros(size(X1,1),3);%记录单价、单位原料转化为产能的比例、供应商最大供应能力 Y(find(X1=="A"),1)=1.2; Y(find(X1=="B"),1)=1.1; Y(find(X1=="C"),1)=1; Y(find(X1=="A"),2)=1/0.6; Y(find(X1=="B"),2)=1/0.66; Y(find(X1=="C"),2)=1/0.72; Y(:,3)=max(X2')';%供应商最大供应能力，正向指标 %我这里随机选择50个，你们的话就用第一问结果 clear X2 aa=randperm(402);aa=aa(1:50); X1=X1(aa,:);Y=Y(aa,:); %% 寻优部分 num=100;%个体数 T0=100;%初始温度 q=0.95;%降温系数 Tmin=1;%最低温度 %初始化种群 x=[]; T=[]; F=[]; for i=1:num     YL=48*28200; %总产能     tt1=[];     tt2=[];     while YL>0 %直到满足产能为止     if YL>56400         z=56400;     else         z=YL;     end     t1=zeros(50,1); %这里是随机给个初始值，方便直接进入while循环 k=[];k=randi([3,50]);%最多选择50个供应商 a=[];a=randperm(50);a=a(1:k);%随机选取供应商 a=sort(a);     while sum(Y(a,2).*Y(a,3).*(1-max(X3(:,1))/100))<z %判断其最大供应量转化为产能是否达标，不能则重新随机         k=[];k=randi([3,50]);%最多选择50个供应商         a=[];a=randperm(50);a=a(1:k);%随机选取供应商         a=sort(a);     end     Min=0;%记录供应量     m=0;%记录对应产能     n=0;     b=[];[~,b]=sort(X1(a),'descend');b=a(b);%按CBA顺序排序，确定Min     while m<z         n=n+1;         if m+Y(b(n),2)*Y(b(n),3)<z             m=m+Y(b(n),2)*Y(b(n),3)*(1-max(X3(:,1))/100);             Min=Min+Y(b(n),3);         else             Min=Min+(z-m)/Y(b(n),2);             m=z;         end     end     c=[];c=Min/sum(Y(a,3));     d=50000;     while sum(d)>48000         d=round((c+(1-c).*rand(k,1)).*Y(a,3));%由于从不同供应商那里订购同一材料价格相同，实则最后就是ABC原料的订购比     end     t1(a,1)=d;%订单     %转运，根据思路将A优先安排给损耗最小的转运商     bb=[];[~,bb]=sort(X1(a));bb=a(bb);     XX3=X3(:,2);     t2=zeros(50,8);     for j=1:length(bb)         f=[];f=t1(bb(j));         while f>0             e=[];e=find(XX3>0);             if XX3(e(1))>=f                 t2(bb(j),x3(e(1)))=f;                 XX3(e(1))=XX3(e(1))-f;                 f=0;             else                 t2(bb(j),x3(e(1)))=XX3(e(1));                 f=f-XX3(e(1));                 XX3(e(1))=0;             end         end     end     YL=YL-sum(t2.*Y(:,2)*(1-XXX3./100)); %将一周的供应量换算为产能     tt1=[tt1,t1];%格式按订购方案表格排列     tt2=[tt2,t2];%格式按转运方案表格排列     end     %记录变量及目标函数     x(i,1)=k;     T{i,1}=tt1;     T{i,2}=tt2;     F(i,1)=k;%供应商数     F(i,2)=2*sum(sum(tt2));%总费用 end [TT,x,T]=ns2_1(x,T,F(:,1),F(:,2)); bestf=TT(1,:); bestx=x(1,:); bestT=T(1,:); figure plot(TT(:,1),TT(:,2),'b*') while T0>Tmin     %初始化种群     xt=[];     Tt=[];     Ft=[];     for i=1:num                  YL=48*28200;         tt1=[];         tt2=[];         while YL>0         if YL>56400             z=56400;         else             z=YL;         end         t1=zeros(50,1);         k=[];k=randi([3,50]);;%这里是随机给个初始值，方便直接进入while循环         a=[];a=randperm(50);a=a(1:k);         a=sort(a);         while sum(Y(a,2).*Y(a,3).*(1-max(X3(:,1))/100))<z %判断其最大供应量转化为产能是否达标，不能则重新随机             k=[];k=randi([3,50]);             a=[];a=randperm(50);a=a(1:k);             a=sort(a);         end         Min=0;%记录供应量         m=0;%记录对应产能         n=0;         b=[];[~,b]=sort(X1(a),'descend');b=a(b);         while m<z             n=n+1;             if m+Y(b(n),2)*Y(b(n),3)<z                 m=m+Y(b(n),2)*Y(b(n),3)*(1-max(X3(:,1))/100);                 Min=Min+Y(b(n),3);             else                 Min=Min+(z-m)/Y(b(n),2);                 m=z;             end         end         c=[];c=Min/sum(Y(a,3));         d=50000;         while sum(d)>48000             d=round((c+(1-c).*rand(k,1)).*Y(a,3));%由于从不同供应商那里订购同一材料价格相同，实则最后就是ABC原料的订购比         end         t1(a,1)=d;%订单         %转运         bb=[];[~,bb]=sort(X1(a));bb=a(bb);         XX3=X3(:,2);         t2=zeros(50,8);         for j=1:length(bb)             f=[];f=t1(bb(j));             while f>0                 e=[];e=find(XX3>0);                 if XX3(e(1))>=f                     t2(bb(j),x3(e(1)))=f;                     XX3(e(1))=XX3(e(1))-f;                     f=0;                 else                     t2(bb(j),x3(e(1)))=XX3(e(1));                     f=f-XX3(e(1));                     XX3(e(1))=0;                 end             end         end         YL=YL-sum(t2.*Y(:,2)*(1-XXX3./100));         tt1=[tt1,t1];         tt2=[tt2,t2];         end         %记录变量及目标函数         xt(i,1)=k;         Tt{i,1}=tt1;         Tt{i,2}=tt2;         Ft(i,1)=k;%供应商数         Ft(i,2)=2*sum(sum(tt2));     end     [TTt,xt,Tt]=ns2_1([x;xt],[T;Tt],[F(:,1);Ft(:,1)],[F(:,2);Ft(:,2)]);     TTt=TTt(1:num,:);     xt=xt(1:num,:);     Tt=Tt(1:num,:);     for kk=1:num         delta=TTt(kk,1)*TTt(kk,2)-TT(kk,1)*TT(kk,2);         if delta<0             TT(kk,:)=TTt(kk,:);             x(kk,:)=xt(kk,:);             T(kk,:)=Tt(kk,:);         else             P=exp(-delta/T0);             if P>rand                 TT(kk,:)=TTt(kk,:);                 x(kk,:)=xt(kk,:);                 T(kk,:)=Tt(kk,:);             end         end     end     bestf=TT(1,:);     bestx=x(1,:);     bestT=T(1,:);     T0=T0*q; end hold on plot(TT(:,1),TT(:,2),'r*') legend('初始分布','最优分布') title('模拟退火寻优-解分布') xlabel('F1 供应商数') ylabel('F2 总费用') %% 最后的结果bestf为最优方案的目标函数，bestx为最少供应商数，bestT中有两个矩阵，均以按附件AB表格排好格式，直接复制过去即可

function y=yongji(H) %计算拥挤度 y1=H(:,1); y2=H(:,2); [yy1,a1]=sort(y1); [yy2,a2]=sort(y2); L=[]; L=[1 1]; for i=2:length(yy1)-1     L=[L;(yy1(i+1,1)-yy1(i-1,1))/(max(yy1)-min(yy1)),(yy2(i+1,1)-yy2(i-1,1))/(max(yy2)-min(yy2))]; end L=[L;1 1]; L=[L(a1,1),L(a2,2)]; y=sum(L,2); end

function [TT,chrom,cchrom]=ns2(x,T,F1,F2) % 快速非支配排序 a = 0; T1 = []; T2 = []; chrom=x; cchrom=T; chrom1 = []; chrom2 = []; cchrom1 = []; cchrom2 = []; while a == 0 %根据被支配数进行分级和排序     M = [];     for i = 1:length(F1)         M(i,1) = length(find(F1<F1(i,1)))+length(find(F2<F2(i,1)));%目标函数最小化这里为<，最大化改成>     end     b1 = [];     b2 = [];     [b1,b2] = sort(M); %b1返回从小到大排序，b2返回原始序号     if  length(chrom)>0 && b1(1) == 0   %无被支配数进入一级用T1矩阵保存         T1 = [T1;F1(b2(1)),F2(b2(1))];         chrom1 = [chrom1;chrom(b2(1),:)];         cchrom1 = [cchrom1;cchrom(b2(1),:)];         F1(b2(1)) = [];         F2(b2(1)) = [];         chrom(b2(1),:) = [];         cchrom(b2(1),:) = [];     else  %有被支配数进入二级用T2矩阵保存         a = 1;         T2 = [F1,F2];         chrom2 = chrom;         cchrom2 = cchrom;     end end T2 = T2(b2,:); chrom2 = chrom2(b2,:); cchrom2 = cchrom2(b2,:); if size(T1,1) > 2  %T1矩阵不用进行拥挤度调整排序，直接对T2进行排序调整即可     y = yongji(T1);%拥挤度     for i = 2:size(T1,1)             if y(i-1) > y(i)                 T1(i-1:1:i,:) = T1(i:-1:i-1,:); %根据拥挤度调整排序，如果后者优于前者则反转顺序                 chrom1(i-1:1:i,:) = chrom1(i:-1:i-1,:);                 cchrom1(i-1:1:i,:) = cchrom1(i:-1:i-1,:);             end     end end if length(T2) > 0  %T1矩阵不用进行拥挤度调整排序，直接对T2进行排序调整即可     y = yongji(T2);%拥挤度     for i = 2:size(T2,1)         if b1(i) == b1(i-1)             if y(i-1) > y(i)                 T2(i-1:1:i,:) = T2(i:-1:i-1,:); %根据拥挤度调整排序，如果后者优于前者则反转顺序                 chrom2(i-1:1:i,:) = chrom2(i:-1:i-1,:);                 cchrom2(i-1:1:i,:) = cchrom2(i:-1:i-1,:);             end         end     end end %排序重组 TT = [T1;T2]; chrom = [chrom1;chrom2]; cchrom = [cchrom1;cchrom2];

第三问程序

 以模拟退火框架写的，可更改为其他优化算法，程序以发布的思路编写的，如有不懂请结合思路理解，程序仅为参考，切勿照搬

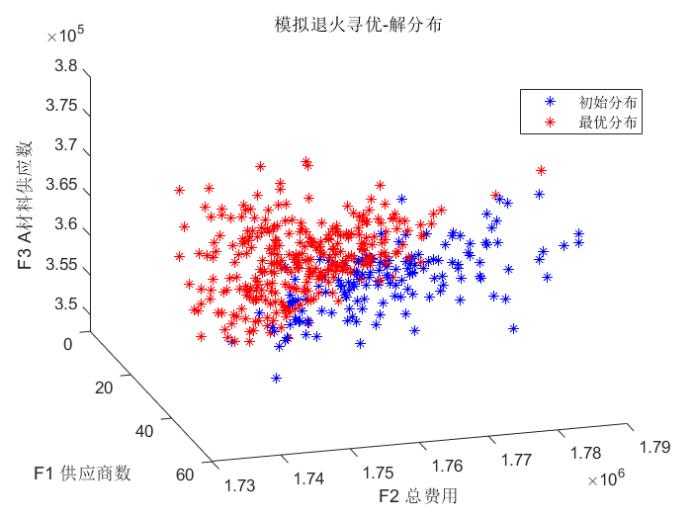
clear %% 第一部分请自行修改为第一问的Top50供应商 %直接运行程序十有八九会报错，因为是随机选的50，请将aa矩阵更改为你们第一问的结果Top50的编号 [~,X1,~]=xlsread('附件1 近5年402家供应商的相关数据.xlsx','企业的订货量（m?）'); X1=string(X1); X1=X1(2:end,2); X2=xlsread('附件1 近5年402家供应商的相关数据.xlsx','供应商的供货量（m?）'); X3=xlsread('附件2 近5年8家转运商的相关数据.xlsx'); X3=mean(X3,2);%这里我直接取平均损耗了 XXX3=X3; [X3,x3]=sort(X3); X3=[X3,6000.*ones(8,1)];%加上最大转运量，方便调用 Y=zeros(size(X1,1),3);%记录单价、单位原料转化为产能的比例、供应商最大供应能力 Y(find(X1=="A"),1)=1.2; Y(find(X1=="B"),1)=1.1; Y(find(X1=="C"),1)=1; Y(find(X1=="A"),2)=1/0.6; Y(find(X1=="B"),2)=1/0.66; Y(find(X1=="C"),2)=1/0.72; Y(:,3)=max(X2')';%供应商最大供应能力，正向指标 %我这里随机选择50个，你们的话就用第一问结果 clear X2 aa=randperm(402);aa=aa(1:50); X1=X1(aa,:);Y=Y(aa,:); %% 寻优部分 num=300;%个体数 T0=100;%初始温度 q=0.95;%降温系数 Tmin=1;%最低温度 %初始化种群 x=[]; T=[]; F=[]; for i=1:num     YL=48*28200; %总产能     tt1=[];     tt2=[];     while YL>0 %直到满足产能为止     if YL>56400         z=56400;     else         z=YL;     end     t1=zeros(50,1);     %这里是随机给个初始值，方便直接进入while循环     k=[];k=randi([3,50]);%最多选择50个供应商     a=[];a=randperm(50);a=a(1:k);%随机选取供应商     a=sort(a);     while sum(Y(a,2).*Y(a,3).*(1-max(X3(:,1))/100))<z %判断其最大供应量转化为产能是否达标，不能则重新随机         k=[];k=randi([3,50]);%最多选择50个供应商         a=[];a=randperm(50);a=a(1:k);%随机选取供应商         a=sort(a);     end     Min=0;%记录供应量     m=0;%记录对应产能     n=0;     b=[];[~,b]=sort(X1(a),'descend');b=a(b);%按CBA顺序排序，确定Min     while m<z         n=n+1;         if m+Y(b(n),2)*Y(b(n),3)<z             m=m+Y(b(n),2)*Y(b(n),3)*(1-max(X3(:,1))/100);             Min=Min+Y(b(n),3);         else             Min=Min+(z-m)/Y(b(n),2);             m=z;         end     end     c=[];c=Min/sum(Y(a,3));     d=50000;     while sum(d)>48000         d=round((c+(1-c).*rand(k,1)).*Y(a,3));%由于从不同供应商那里订购同一材料价格相同，实则最后就是ABC原料的订购比     end     t1(a,1)=d;%订单     %转运，根据思路将A优先安排给损耗最小的转运商     bb=[];[~,bb]=sort(X1(a));bb=a(bb);     XX3=X3(:,2);     t2=zeros(50,8);     for j=1:length(bb)         f=[];f=t1(bb(j));         while f>0             e=[];e=find(XX3>0);             if XX3(e(1))>=f                 t2(bb(j),x3(e(1)))=f;                 XX3(e(1))=XX3(e(1))-f;                 f=0;             else                 t2(bb(j),x3(e(1)))=XX3(e(1));                 f=f-XX3(e(1));                 XX3(e(1))=0;             end         end     end     YL=YL-sum(t2.*Y(:,2)*(1-XXX3./100)); %将一周的供应量换算为产能     tt1=[tt1,t1];%格式按订购方案表格排列     tt2=[tt2,t2];%格式按转运方案表格排列     end     %记录变量及目标函数     x(i,1)=k;     T{i,1}=tt1;     T{i,2}=tt2;     F(i,1)=k;%供应商数     F(i,2)=2*sum(sum(tt2));%总费用     F(i,3)=sum(sum(tt1(find(X1=="A"),:)));%A材料     F(i,4)=sum(sum(tt1(find(X1=="C"),:)));%C材料 end [TT,x,T]=ns2_2(x,T,F(:,1),F(:,2),F(:,3),F(:,4)); bestf=TT(1,:); bestx=x(1,:); bestT=T(1,:); figure plot3(TT(:,1),TT(:,2),TT(:,3),'b*') while T0>Tmin     %初始化种群     xt=[];     Tt=[];     Ft=[];     for i=1:num                  YL=48*28200;         tt1=[];         tt2=[];         while YL>0         if YL>56400             z=56400;         else             z=YL;         end         t1=zeros(50,1);         k=[];k=randi([3,50]);         a=[];a=randperm(50);a=a(1:k);         a=sort(a);%这里是随机给个初始值，方便直接进入while循环         while sum(Y(a,2).*Y(a,3).*(1-max(X3(:,1))/100))<z %判断其最大供应量转化为产能是否达标，不能则重新随机             k=[];k=randi([3,50]);             a=[];a=randperm(50);a=a(1:k);             a=sort(a);         end         Min=0;%记录供应量         m=0;%记录对应产能         n=0;         b=[];[~,b]=sort(X1(a),'descend');b=a(b);         while m<z             n=n+1;             if m+Y(b(n),2)*Y(b(n),3)<z                 m=m+Y(b(n),2)*Y(b(n),3)*(1-max(X3(:,1))/100);                 Min=Min+Y(b(n),3);             else                 Min=Min+(z-m)/Y(b(n),2);                 m=z;             end         end         c=[];c=Min/sum(Y(a,3));         d=50000;         while sum(d)>48000             d=round((c+(1-c).*rand(k,1)).*Y(a,3));%由于从不同供应商那里订购同一材料价格相同，实则最后就是ABC原料的订购比         end         t1(a,1)=d;%订单         %转运         bb=[];[~,bb]=sort(X1(a));bb=a(bb);         XX3=X3(:,2);         t2=zeros(50,8);         for j=1:length(bb)             f=[];f=t1(bb(j));             while f>0                 e=[];e=find(XX3>0);                 if XX3(e(1))>=f                     t2(bb(j),x3(e(1)))=f;                     XX3(e(1))=XX3(e(1))-f;                     f=0;                 else                     t2(bb(j),x3(e(1)))=XX3(e(1));                     f=f-XX3(e(1));                     XX3(e(1))=0;                 end             end         end         YL=YL-sum(t2.*Y(:,2)*(1-XXX3./100));         tt1=[tt1,t1];         tt2=[tt2,t2];         end         %记录变量及目标函数         xt(i,1)=k;         Tt{i,1}=tt1;         Tt{i,2}=tt2;         Ft(i,1)=k;%供应商数         Ft(i,2)=2*sum(sum(tt2));%总费用         Ft(i,3)=sum(sum(tt1(find(X1=="A"),:)));%A材料         Ft(i,4)=sum(sum(tt1(find(X1=="C"),:)));%C材料     end     [TTt,xt,Tt]=ns2_2([x;xt],[T;Tt],[F(:,1);Ft(:,1)],[F(:,2);Ft(:,2)],[F(:,3);Ft(:,3)],[F(:,4);Ft(:,4)]);     TTt=TTt(1:num,:);     xt=xt(1:num,:);     Tt=Tt(1:num,:);     for kk=1:num         delta=TTt(kk,3)/(TTt(kk,1)*TTt(kk,2)*TTt(kk,4))-TT(kk,3)/(TT(kk,1)*TT(kk,2)*TT(kk,4));         if delta<0             TT(kk,:)=TTt(kk,:);             x(kk,:)=xt(kk,:);             T(kk,:)=Tt(kk,:);         else             P=exp(-delta/T0);             if P>rand                 TT(kk,:)=TTt(kk,:);                 x(kk,:)=xt(kk,:);                 T(kk,:)=Tt(kk,:);             end         end     end     bestf=TT(1,:);     bestx=x(1,:);     bestT=T(1,:);     T0=T0*q; end hold on plot3(TT(:,1),TT(:,2),TT(:,3),'r*') legend('初始分布','最优分布') title('模拟退火寻优-解分布') xlabel('F1 供应商数') ylabel('F2 总费用') zlabel('F3 A材料供应数') %% 最后的结果bestf为最优方案的目标函数，bestx为最少供应商数，bestT中有两个矩阵，均以按附件AB表格排好格式，直接复制过去即可

function [TT,chrom,cchrom]=ns2(x,T,F1,F2,F3,F4) % 快速非支配排序 a = 0; T1 = []; T2 = []; chrom=x; cchrom=T; chrom1 = []; chrom2 = []; cchrom1 = []; cchrom2 = []; while a == 0 %根据被支配数进行分级和排序     M = [];     for i = 1:length(F1)         M(i,1) = length(find(F1<F1(i,1)))+length(find(F2<F2(i,1)))+length(find(F3>F3(i,1)))+length(find(F4<F4(i,1)));%目标函数最小化这里为<，最大化改成>     end     b1 = [];     b2 = [];     [b1,b2] = sort(M); %b1返回从小到大排序，b2返回原始序号     if  length(chrom)>0 && b1(1) == 0   %无被支配数进入一级用T1矩阵保存         T1 = [T1;F1(b2(1)),F2(b2(1)),F3(b2(1)),F4(b2(1))];         chrom1 = [chrom1;chrom(b2(1),:)];         cchrom1 = [cchrom1;cchrom(b2(1),:)];         F1(b2(1)) = [];         F2(b2(1)) = [];         F3(b2(1)) = [];         F4(b2(1)) = [];         chrom(b2(1),:) = [];         cchrom(b2(1),:) = [];     else  %有被支配数进入二级用T2矩阵保存         a = 1;         T2 = [F1,F2,F3,F4];         chrom2 = chrom;         cchrom2 = cchrom;     end end T2 = T2(b2,:); chrom2 = chrom2(b2,:); cchrom2 = cchrom2(b2,:); if size(T1,1) > 2  %T1矩阵不用进行拥挤度调整排序，直接对T2进行排序调整即可     y = yongji(T1);%拥挤度     for i = 2:size(T1,1)             if y(i-1) > y(i)                 T1(i-1:1:i,:) = T1(i:-1:i-1,:); %根据拥挤度调整排序，如果后者优于前者则反转顺序                 chrom1(i-1:1:i,:) = chrom1(i:-1:i-1,:);                 cchrom1(i-1:1:i,:) = cchrom1(i:-1:i-1,:);             end     end end if length(T2) > 0  %T1矩阵不用进行拥挤度调整排序，直接对T2进行排序调整即可     y = yongji(T2);%拥挤度     for i = 2:size(T2,1)         if b1(i) == b1(i-1)             if y(i-1) > y(i)                 T2(i-1:1:i,:) = T2(i:-1:i-1,:); %根据拥挤度调整排序，如果后者优于前者则反转顺序                 chrom2(i-1:1:i,:) = chrom2(i:-1:i-1,:);                 cchrom2(i-1:1:i,:) = cchrom2(i:-1:i-1,:);             end         end     end end %排序重组 TT = [T1;T2]; chrom = [chrom1;chrom2]; cchrom = [cchrom1;cchrom2];

function y=yongji(H) %计算拥挤度 y1=H(:,1); y2=H(:,2); [yy1,a1]=sort(y1); [yy2,a2]=sort(y2); L=[]; L=[1 1]; for i=2:length(yy1)-1     L=[L;(yy1(i+1,1)-yy1(i-1,1))/(max(yy1)-min(yy1)),(yy2(i+1,1)-yy2(i-1,1))/(max(yy2)-min(yy2))]; end L=[L;1 1]; L=[L(a1,1),L(a2,2)]; y=sum(L,2); end