P3302 SDOI2013森林

Posted 2021-09-25 Jozky86

P3302 [SDOI2013]森林

题意：

一片森林，有n个节点，m个边，现在有t个操作，
Q x y k：Q x y k 查询点 x 到点 y 路径上所有的权值中，第 ·k 小的权值是多少
L x y 在点 x 和点 y 之间连接一条边。保证完成此操作后，仍然是一片森林。
必须在线操作

题解：

算是这个题P2633 Count on a tree的延申，这个题是求点x与点y路径上的第k小权值，本题多了一个合并操作。
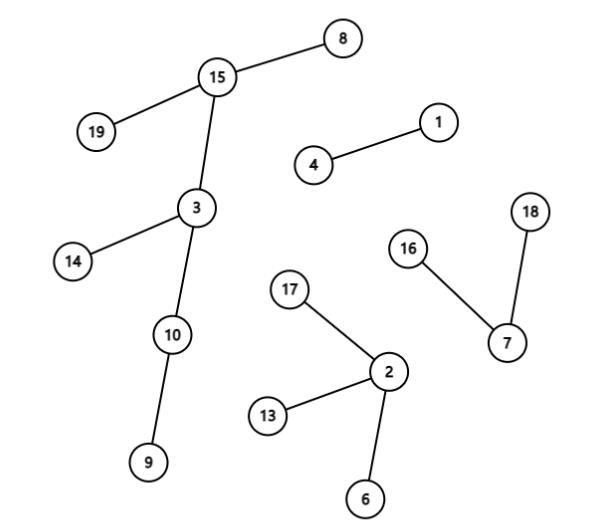
合并我是这样想的：如图，如果我们要合并点10和点13，我想的是直接让13的父亲节点为10，但是这样直接连复杂度不行，所以我们要采取启发式合并的思想。对于点x和点y，让小树接到大树上，重构小树中的主席树、LCA相关数组，这样保证了每次重构的工作量是最少的(log n)。
重构就是dfs被加入的小树，然后更新小树的主席树，深度，倍增fa等信息

思路很简单，难在调试啊
我调了半天都没对emm
详细细节看代码，感觉代码写的还是很清晰明了

代码：

#include <bits/stdc++.h>
#include <unordered_map>
#define debug(a, b) printf("%s = %d\\n", a, b);
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;
clock_t startTime, endTime;
//Fe~Jozky
const ll INF_ll= 1e18;
const int INF_int= 0x3f3f3f3f;
void read(){};
template <typename _Tp, typename... _Tps> void read(_Tp& x, _Tps&... Ar)
{
    x= 0;
    char c= getchar();
    bool flag= 0;
    while (c < '0' || c > '9')
        flag|= (c == '-'), c= getchar();
    while (c >= '0' && c <= '9')
        x= (x << 3) + (x << 1) + (c ^ 48), c= getchar();
    if (flag)
        x= -x;
    read(Ar...);
}
template <typename T> inline void write(T x)
{
    if (x < 0) {
        x= ~(x - 1);
        putchar('-');
    }
    if (x > 9)
        write(x / 10);
    putchar(x % 10 + '0');
}
void rd_test()
{
#ifdef ONLINE_JUDGE
#else
    startTime= clock();
    freopen("data.in", "r", stdin);
#endif
}
void Time_test()
{
#ifdef ONLINE_JUDGE
#else
    endTime= clock();
    printf("\\nRun Time:%lfs\\n", (double)(endTime - startTime) / CLOCKS_PER_SEC);
#endif
}
const int maxn= 8e4 + 5;
int T, n, m, TT, lastans;
int tot, row[maxn], s[maxn], size[maxn];
int find_rt[maxn], lg[maxn], fa[maxn][35], deep[maxn];
struct Tree
{
    int ls, rs, siz;
} rt[105 * maxn];
int root[maxn], top;
vector<int> vec[maxn];
void pre_work()
{
    lg[0]= -1;
    read(T, n, m, TT);
    for (int i= 1; i <= n; i++) {
        read(row[i]);
        s[i]= row[i];
        lg[i]= lg[i >> 1] + 1;
        find_rt[i]= i;
    }
    //离散化处理
    sort(row + 1, row + 1 + n);
    tot= unique(row + 1, row + 1 + n) - (row + 1);
    for (int i= 1; i <= n; i++)
        s[i]= lower_bound(row + 1, row + 1 + tot, s[i]) - row;

    for (int i= 1; i <= m; i++) {
        int u, v;
        read(u, v);
        vec[u].push_back(v);
        vec[v].push_back(u);
    }
}

void build(int& pos, int pre, int l, int r, int val)
{
    pos= ++top;
    rt[pos]= rt[pre];
    rt[pos].siz++;
    if (l == r)
        return;
    int mid= (l + r) >> 1;
    if (val <= mid)
        build(rt[pos].ls, rt[pre].ls, l, mid, val);
    else
        build(rt[pos].rs, rt[pre].rs, mid + 1, r, val);
}

void dfs(int u, int f, int rt)
{
    build(root[u], root[f], 1, tot, s[u]); //建立主席树

    deep[u]= deep[f] + 1; //求深度
    fa[u][0]= f; //求倍增fa
    size[rt]++; //记录子树数量
    find_rt[u]= rt; //记录根节点

    for (int i= 1; i <= 18; i++) //每次更新倍增
        fa[u][i]= fa[fa[u][i - 1]][i - 1];
    for (auto v : vec[u]) {
        if (v == f)
            continue;
        dfs(v, u, rt);
    }
}

int LCA(int u, int v)
{
    if (deep[u] < deep[v])
        swap(u, v);
    while (deep[u] > deep[v])
        u= fa[u][lg[deep[u] - deep[v]]];
    if (u == v)
        return u;
    for (int i= lg[deep[u]]; i >= 0; i--)
        if (fa[u][i] != fa[v][i])
            u= fa[u][i], v= fa[v][i];
    return fa[u][0];
}

int query(int u, int v, int lca, int fa_lca, int l, int r, int k)
{
    //主席树查询第k小值
    if (l == r)
        return row[l];
    int sum= rt[rt[u].ls].siz + rt[rt[v].ls].siz - rt[rt[lca].ls].siz - rt[rt[fa_lca].ls].siz;
    int mid= (l + r) >> 1;
    if (k <= sum)
        return query(rt[u].ls, rt[v].ls, rt[lca].ls, rt[fa_lca].ls, l, mid, k);
    return query(rt[u].rs, rt[v].rs, rt[lca].rs, rt[fa_lca].rs, mid + 1, r, k - sum);
}

int main()
{
    rd_test();

    pre_work(); //预处理前置工作
    for (int i= 1; i <= n; i++)
        if (find_rt[i] == i)
            dfs(i, 0, i);
    char ch[5];
    int x, y, k;
    for (int i= 1; i <= TT; i++) {
        scanf("%s", ch);
        read(x, y);
        x^= lastans;
        y^= lastans;
        if (ch[0] == 'Q') {
            read(k);
            k^= lastans;
            int lca= LCA(x, y);
            int fa_lca= fa[lca][0];
            lastans= query(root[x], root[y], root[lca], root[fa_lca], 1, tot, k);
            printf("%d\\n", lastans);
        }
        else {
            vec[x].push_back(y);
            vec[y].push_back(x);
            int fx= find_rt[x], fy= find_rt[y];
            if (size[fy] < size[fx]) {
                dfs(y, x, fx);
            }
            else {
                dfs(x, y, fy);
            }
        }
    }
    return 0;
}