Leetcode——克隆图

Posted 2021-09-25 Yawn,

1. 克隆图

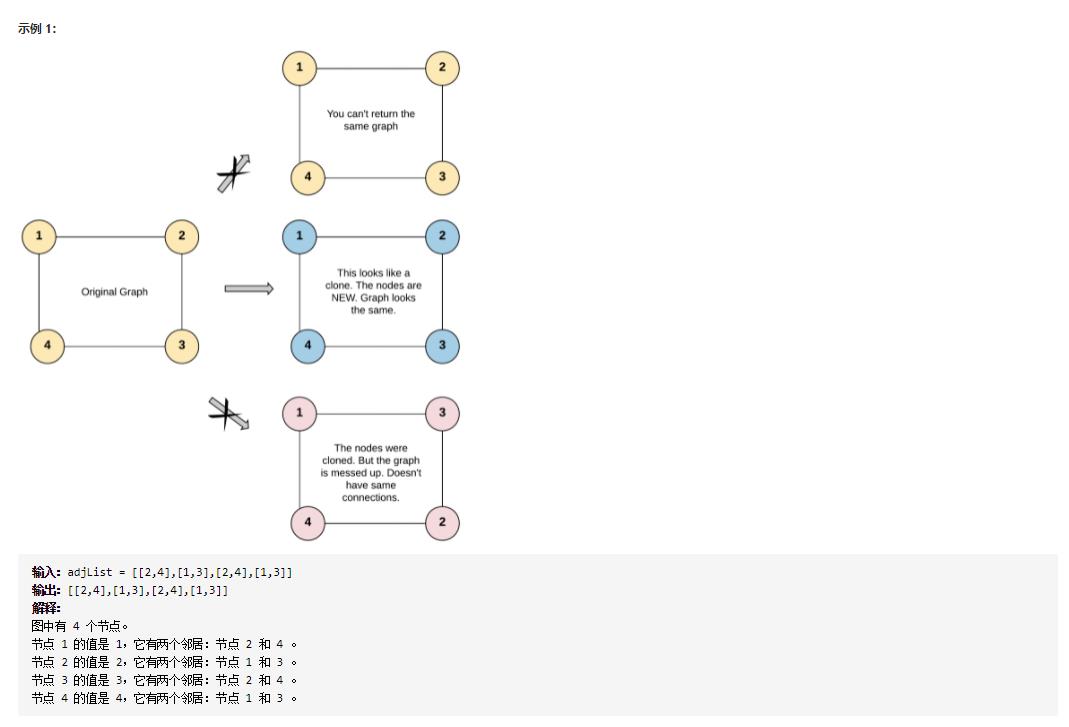
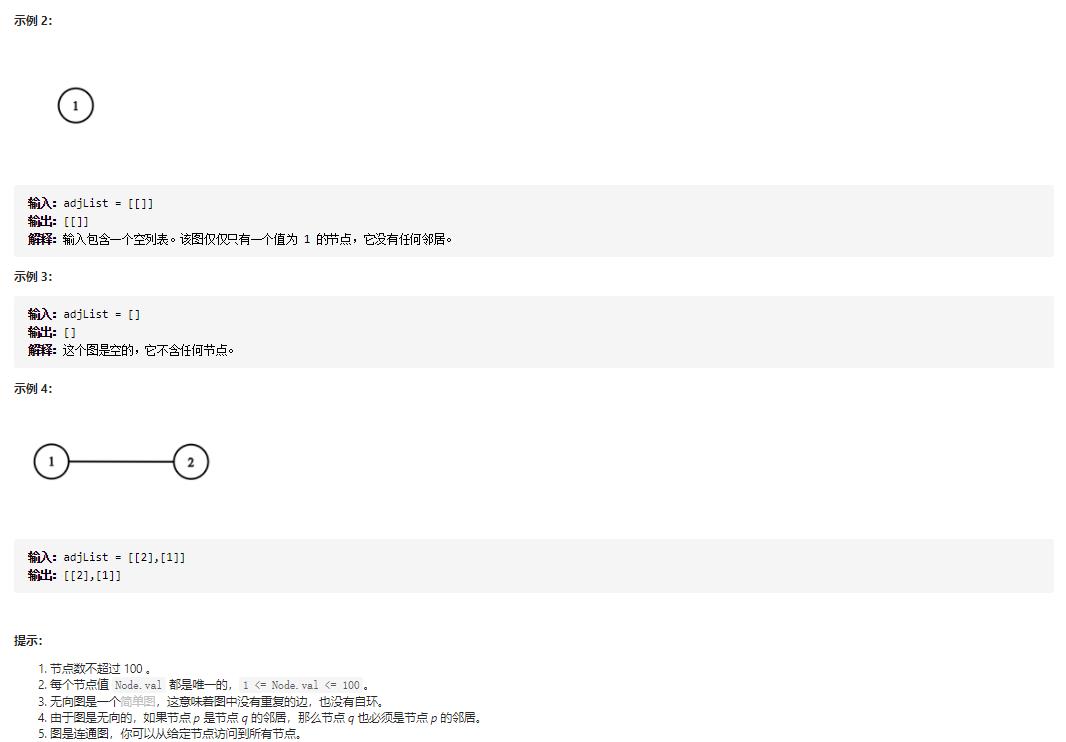
（1）DFS

• 这道题的这种解决方法和一个克隆链表的题目很像，其中 Node 中的一个指针随机指向链表中的任意一个节点。
• 解决方法就是，先顺序遍历节点，然后记录实体和克隆 Node 的映射对。 然后再次遍历链表，通过映射关系再为克隆链表指向映射的随机节点。

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> neighbors;
    public Node() {
        val = 0;
        neighbors = new ArrayList<Node>();
    }
    public Node(int _val) {
        val = _val;
        neighbors = new ArrayList<Node>();
    }
    public Node(int _val, ArrayList<Node> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
}
*/

class Solution {
    public Node cloneGraph(Node node) {
        //遍历时候要记录已经访问点，我们用一个Map记录。
        Map<Node, Node> map = new HashMap<>();
        return dfs(node, map);
    }

    private Node dfs(Node node, Map<Node, Node> map) {
        if (node == null) 
            return null;

        //已经遍历过该节点，直接返回
        if (map.containsKey(node)) 
            return map.get(node);

        //克隆新节点,并将该节点加入map中
        Node clone = new Node(node.val, new ArrayList<>());
        map.put(node, clone);

        //连接它的邻居节点，并继续遍历邻居节点的邻居
        for (Node n : node.neighbors)
            clone.neighbors.add(dfs(n, map));
        
        //返回克隆节点
        return clone;
    }
}

（2）BFS

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> neighbors;
    public Node() {
        val = 0;
        neighbors = new ArrayList<Node>();
    }
    public Node(int _val) {
        val = _val;
        neighbors = new ArrayList<Node>();
    }
    public Node(int _val, ArrayList<Node> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
}
*/

class Solution {
    public Node cloneGraph(Node node) {
        if (node == null)
            return null;
        
        //遍历时候要记录已经访问点，我们用一个Map记录。
        Map<Node, Node> map = new HashMap<>();

        //创建第一个克隆节点，并加入map
        Node clone = new Node(node.val, new ArrayList<>());
        map.put(node, clone);

        //存放每个节点
        Deque<Node> queue = new LinkedList<>();
        queue.offer(node);

        while (!queue.isEmpty()) {
            //依次弹出每个节点
            Node tmp = queue.poll();
            for (Node n : tmp.neighbors) {
                //未遍历过该节点，克隆新节点,并将该节点加入map中
                if (!map.containsKey(n)) {
                    map.put(n, new Node(n.val, new ArrayList<>()));
                    queue.offer(n);
                }
                //已遍历过该节点，将直接获取遍历到的n节点的克隆节点 加入到 当前取出节点的克隆节点的邻居节点表中
                map.get(tmp).neighbors.add(map.get(n));
            }
        }
        //返回初始克隆节点
        return clone;
    }
}