Leetcode——长度最小的子数组 / 最短无序连续子数组 / 和为k的连续子数组

Posted 2021-09-25 Yawn,

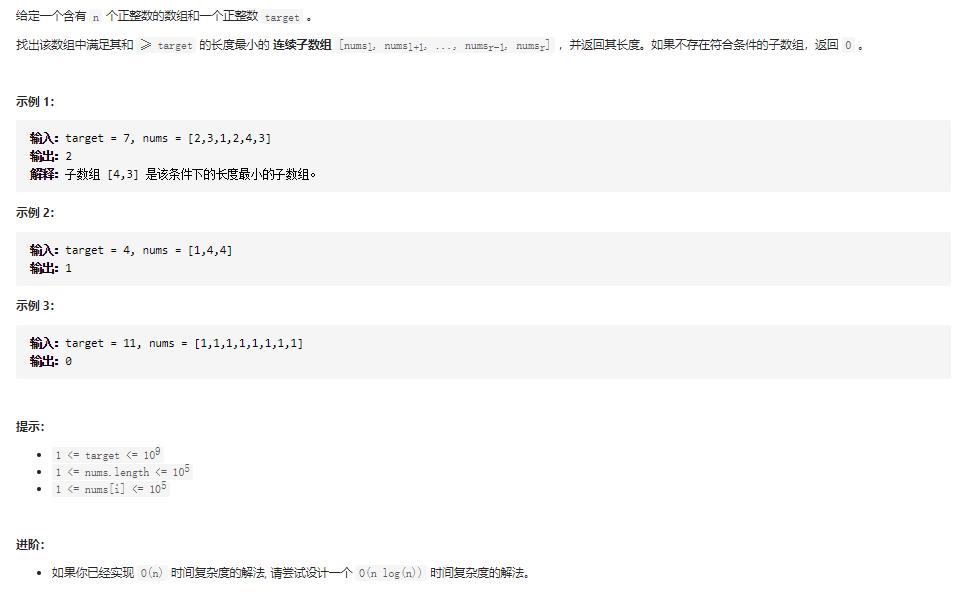
1. 长度最小的子数组

（1）暴力

使用两个 for 循环，一个 for 循环固定一个数字比如 m，另一个 for 循环从 m 的下一个元素开始累加，当和大于等于 s 的时候终止内层循环，顺便记录下最小长度

class Solution {
    public int minSubArrayLen(int s, int[] nums) {
        int min = Integer.MAX_VALUE;
        for (int i = 0; i < nums.length; i++) {
            int sum = nums[i];
            //如果一个数字就大于s，直接返回即可
            if (sum >= s)
                return 1;
            for (int j = i + 1; j < nums.length; j++) {
                sum += nums[j];
                if (sum >= s) {
                    min = Math.min(min, j - i + 1);
                    break;
                }
            }
        }

        if (min == Integer.MAX_VALUE)
            return 0;
        else
            return min;
    }
}

（2）滑动窗口

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int left = 0;
        int min = nums.length + 1;  //为了判断不存在数组和 >= target的情况
        int sum = 0;

        for (int right = 0; right < nums.length; right++) {
            sum = sum + nums[right];
            while (sum >= target) {
                if (right - left + 1 < min) {
                    min = right - left + 1;
                }

                sum = sum - nums[left];
                left++;
            }
        }
        
        //min大于数组长度，返回0
        if (min > nums.length)
            return 0;
        else
            return min;
    }
}

2. 最短无序连续子数组

（1）双指针 + 排序

最终目的是让整个数组有序，那么我们可以先将数组拷贝一份进行排序，然后使用两个指针 i 和 j 分别找到左右两端第一个不同的地方，那么 [i, j] 这一区间即是答案。

• 时间复杂度：O(nlogn)
• 空间复杂度：O(n)

class Solution {
    public int findUnsortedSubarray(int[] nums) {
        int n = nums.length;
        int[] arr = nums.clone();
        Arrays.sort(arr);
        int i = 0, j = n - 1;
        while (i <= j && nums[i] == arr[i]) 
        	i++;
        while (i <= j && nums[j] == arr[j]) 
        	j--;
        return j - i + 1;
    }
}

（2）双指针 + 线性扫描

另外一个做法是，我们把整个数组分成三段处理。

• 时间 O(n) ，空间 O(1)
• 起始时，先通过双指针 i 和 j 找到左右两次侧满足 单调递增 的分割点。
• 即此时 [0, i] 和 [j, n)满足升序要求，而中间部分 (i, j) 不确保有序。
• 然后我们对中间部分 [i, j]进行遍历：
  • 发现 nums[x] < nums[i - 1]：由于对 [i, j] 部分进行排序后 nums[x] 会出现在 nums[i - 1]后，将不满足整体升序，此时我们需要调整分割点 i 的位置；
  • 发现 nums[x] > nums[j + 1]：由于对 [i, j]部分进行排序后 nums[x] 会出现在 nums[j + 1] 前，将不满足整体升序，此时我们需要调整分割点 j 的位置。

在调整 i 和 j 的时候，我们可能会到达数组边缘，这时候可以建立两个哨兵：数组左边存在一个足够小的数，数组右边存在一个足够大的数。

思路过程：

通过双指针 i 和 j 找到左右两侧满足 单调递增 的分割点。
比如 [2,6,4,8,10,9,15] 找到的 i => 1, j => 5; nums[1] = 6, nums[5] = 9
对找到的分割点 i, j ; [0,i] 和 [j,n) 都是单调递增的，中间部分 (i + 1,j - 1) 不确保有序。

记录下初始的分割点 l = i, r = j,  对中间部分 [l,r] 遍历调整分割点，
[2,6,4,8,10,9,15] 

【6,4,8,10,9】
	l = i = 1 对应 6	
	r = j = 5 对应9

对 nums[k](l <= k <= r) ：
	若 nums[k] < nums[i], i 向左调整一位,  
	若 nums[k] > nums[j], j 向右调整一位  

遍历完中间部分，左右分割点 i ,j 之前的子数组 [i + 1, j - 1] 就是最终求的最短无序连续子数组

实现代码：

class Solution {
    int MIN = -100005, MAX = 100005;
    public int findUnsortedSubarray(int[] nums) {
        int n = nums.length;
        int i = 0, j = n - 1;
        
		// 通过双指针 i 和 j 找到左右两侧满足 单调递增 的分割点。
        // [0,i] 和 [j,n) 都是单调递增的，中间部分 (i,j) 不确保有序。
        while (i < j && nums[i] <= nums[i + 1]) i++;
        while (i < j && nums[j] >= nums[j - 1]) j--;
		
		//nums[x] < nums[i - 1]：由于对 [i + 1, j - 1] 部分进行排序后 nums[x] 会出现在 nums[i - 1]后，将不满足整体升序，此时我们需要调整分割点 i 的位置；
		//[2,6,4,8,10,9,15]  【6,4,8,10,9】 也就是 4 < 6
        int l = i, r = j;
        int min = nums[i], max = nums[j];
        for (int u = l; u <= r; u++) {
            if (nums[u] < min) {		
                while (i >= 0 && nums[i] > nums[u]) //调整分割点 i
                	i--;
                min = i >= 0 ? nums[i] : MIN;
            }
            if (nums[u] > max) {
                while (j < n && nums[j] < nums[u]) // 调整分割点 j
                	j++;
                max = j < n ? nums[j] : MAX;
            }
        }
        // [i + 1, j - 1] 就是最短无序连续子数组
        return j == i ? 0 : (j - 1) - (i + 1) + 1;
    }
}

（3）单调栈

• 维护一个单调递减栈，保证栈顶下标元素一定是当前栈中最大的。
• 从左往右扫一遍找到左边界，再从右往左扫一遍找到右边界，两者相减即可。

class Solution {
    public int findUnsortedSubarray(int[] nums) {
        // 单调栈从前往后遍历一遍可得到左边界
        // 单调栈从后往前遍历一遍可得到右边界
        Deque<Integer> stack = new ArrayDeque<>();
        int left = nums.length;
        for (int i = 0; i < nums.length; i++) {
            while (!stack.isEmpty() && nums[stack.peek()] > nums[i]) {
                left = Math.min(left, stack.pop());
            }
            stack.push(i);
        }

        stack.clear();
        int right = -1;
        for (int i = nums.length - 1; i >= 0; i--) {
            while (!stack.isEmpty() && nums[stack.peek()] < nums[i]) {
                right = Math.max(right, stack.pop());
            }
            stack.push(i);
        }

        return right - left > 0 ? right - left + 1 : 0;
    }
}

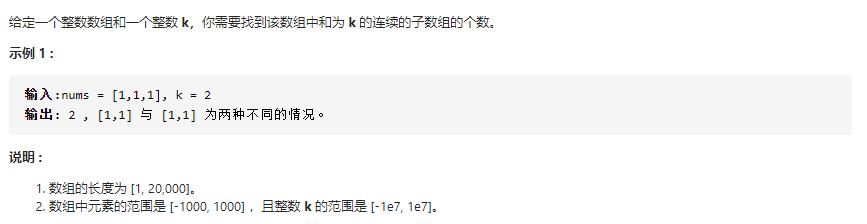
3. 和为k的连续子数组

（1）暴力

考虑：

• 元素是否存在负数
• 需要连续子数组

class Solution {
    public int subarraySum(int[] nums, int k) {
        int len = nums.length;
        int count = 0;
        for (int left = 0; left < len; left++) {
            for (int right = left; right < len; right++) {
                int sum = 0;
                for (int i = left; i <= right; i++) {
                    sum += nums[i];
                }
                if (sum == k) {
                    count++;
                }
            }
        }
        return count;
    }

}

（2）暴力（优化）

• 固定了起点，即先固定左边界，然后枚举右边界哈，时间复杂度降了一维。

class Solution {
    public int subarraySum(int[] nums, int k) {
        int count = 0;
        int len = nums.length;
        for (int left = 0; left < len; left++) {
            int sum = 0;
            // 区间里可能会有一些互相抵销的元素
            for (int right = left; right < len; right++) {
                sum += nums[right];
                if (sum == k) {
                    count++;
                }
            }
        }
        return count;
    }
}

或者：

class Solution {
    public int subarraySum(int[] nums, int k) {
         int len = nums.length;
         int sum = 0;
         int count = 0;
         //双重循环
         for (int i = 0; i < len; ++i) {
             for (int j = i; j < len; ++j) {
                 sum += nums[j];
                 //发现符合条件的区间
                 if (sum == k) {
                     count++;
                 }
             }
             //记得归零，重新遍历
             sum = 0;
         }
         return count;
    }
}

（3）前缀和

• 前缀和其实我们很早之前就了解过的，我们求数列的和时，Sn = a1+a2+a3+…an; 此时Sn就是数列的前 n 项和。

• 例 S5 = a1 + a2 + a3 + a4 + a5; S2 = a1 + a2。所以我们完全可以通过 S5-S2 得到 a3+a4+a5 的值，这个过程就和我们做题用到的前缀和思想类似。我们的前缀和数组里保存的就是前 n 项的和。
  

• 我们通过前缀和数组保存前 n 位的和，presum[1]保存的就是 nums 数组中前 1 位的和，也就是 presum[1] = nums[0], presum[2] = nums[0] + nums[1] = presum[1] + nums[1]. 依次类推，所以我们通过前缀和数组可以轻松得到每个区间的和。

• 例如我们需要获取 nums[2] 到 nums[4] 这个区间的和，我们则完全根据 presum 数组得到，是不是有点和我们之前说的字符串匹配算法中 BM,KMP 中的 next 数组和 suffix 数组作用类似。那么我们怎么根据 presum 数组获取 nums[2] 到 nums[4] 区间的和呢？见下图
  
  我们可以通过下面这段代码得到我们的前缀和数组，非常简单：

 for (int i = 0; i < nums.length; i++) {
      presum[i+1] = nums[i] + presum[i];
 }

我们看看直接使用前缀和怎么写

class Solution {
    public int subarraySum(int[] nums, int k) {
        //前缀和数组
        int[] presum = new int[nums.length+1];
        for (int i = 0; i < nums.length; i++) {
            //这里需要注意，我们的前缀和是presum[1]开始填充的
            presum[i+1] = nums[i] + presum[i];
        }
        //统计个数
        int count = 0;
        for (int i = 0; i < nums.length; ++i) {
            for (int j = i; j < nums.length; ++j) {
                //注意偏移，因为我们的nums[2]到nums[4]等于presum[5]-presum[2]
                //所以这样就可以得到nums[i,j]区间内的和
                if (presum[j+1] - presum[i] == k) {
                    count++;
                }
            }
        }
        return count;
    }
}

直接使用前缀和，发现该代码虽然用到了前缀和数组，但是对比暴力法并没有提升性能，时间复杂度仍为O(n^2)，空间复杂度成了 O(n)。那我们有没有其他方法解决呢？

（4）前缀和 + 哈希表优化

由于只关心次数，不关心具体的解，我们可以使用哈希表加速运算；

由于保存了之前相同前缀和的个数，计算区间总数的时候不是一个一个地加，时间复杂度降到了 O(N)

解释一开始 preSumFreq.put(0, 1); 的意义

• 计算完包括了当前数前缀和以后，我们去查一查在当前数之前，有多少个前缀和等于 preSum - k 呢？
  这是因为满足 preSum - (preSum - k) == k 的区间的个数是我们所关心的。

• 对于一开始的情况，下标 0 之前没有元素，可以认为前缀和为 0，个数为 1 个，
  因此 preSumFreq.put(0, 1);，这一点是必要且合理的。

class Solution {
    public int subarraySum(int[] nums, int k) {
        // key：前缀和，value：key 对应的前缀和的个数
        Map<Integer, Integer> preSumFreq = new HashMap<>();
        // 对于下标为 0 的元素，前缀和为 0，个数为 1
        preSumFreq.put(0, 1);

        int preSum = 0;
        int count = 0;
        for (int num : nums) {
            preSum += num;

            // 先获得前缀和为 preSum - k 的个数，加到计数变量里
            if (preSumFreq.containsKey(preSum - k)) {
                count += preSumFreq.get(preSum - k);
            }

            // 然后维护 preSumFreq 的定义
            preSumFreq.put(preSum, preSumFreq.getOrDefault(preSum, 0) + 1);
        }
        
        return count;
    }
}