Leetcode——重叠区间(会议室1,2) / 合并区间 / 插入区间
Posted Yawn,
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Leetcode——重叠区间(会议室1,2) / 合并区间 / 插入区间相关的知识,希望对你有一定的参考价值。
1. 会议室 (重叠区间)
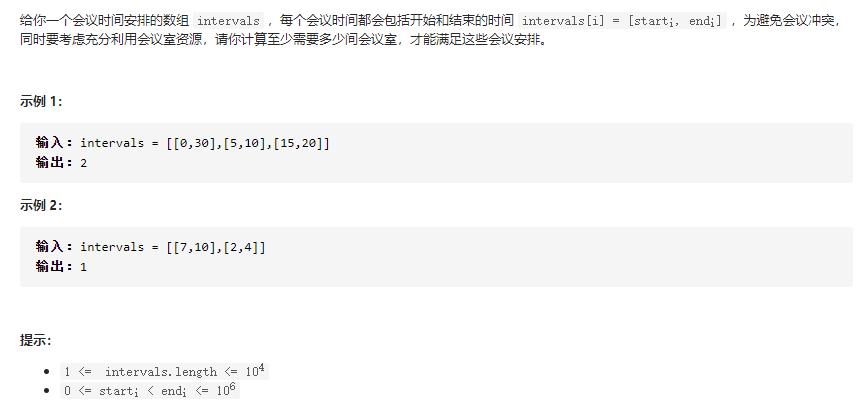
给定一个会议时间安排的数组 intervals ,每个会议时间都会包括开始和结束的时间 intervals[i] = [starti, endi] ,请你判断一个人是否能够参加这里面的全部会议。
示例 1::
输入: intervals = [[0,30],[5,10],[15,20]]
输出: false
解释: 存在重叠区间,一个人在同一时刻只能参加一个会议。
示例 2::
输入: intervals = [[7,10],[2,4]]
输出: true
解释: 不存在重叠区间。
(1)排序
因为一个人在同一时刻只能参加一个会议,因此题目实质是判断是否存在重叠区间,这个简单,将区间按照会议开始时间进行排序,然后遍历一遍判断即可
class Solution {
public boolean canAttendMeetings(int[][] intervals) {
// 将区间按照会议开始实现升序排序
Arrays.sort(intervals, (o1, o2) -> o1[0] - o2[0]);
//如果下一个会议在前一个会议结束之前就开始了,返回 false。
for (int i = 1; i < intervals.length; i++) {
if (intervals[i][0] < intervals[i - 1][1])
return false;
}
return true;
}
}
2. 会议室2 (重叠区间)
(1)优先队列
基本思路:
- 如果我们能统计出每一个时刻要开会的会议数量,就能知道各时刻对于会议室数量的需求,则会议最繁忙的那个时刻需要的会议室数量就是我们想要的结果。只要我们的会议室数量满足了这个时刻的开会需求,则其他时刻都能够满足。
算法流程:
- 因为我们要按时间顺序遍历,所以先将数组按照会议的开始时间排序
- 准备一个最小堆,堆中元素为每一个正在进行中会议的结束时间
- 遍历数组,如果发现在当前时刻,有已经过了结束时间但还在堆中的会议,便将其从堆中弹出。之后将- 当前的会议加入到堆中
- 在遍历过程中不断统计堆中元素的数量,这个数量代表一个时刻正在进行中的会议数量,也即对会议室数量的需求,这个需求的最大值即为结果。
class Solution {
//本题主要思路:找到某时刻能同时进行的会议数量,那么这个最大的同时刻会议数量就是需要的最大会议室数量
//利用优先队列(小顶堆)来保存同时进行的会议,队列的最大size就是会议数量
public int minMeetingRooms(int[][] intervals) {
//判空操作
if (intervals.length < 1)
return 0;
//建立优先队列,默认小顶堆
PriorityQueue<Integer> queue=new PriorityQueue<>();
//对会议开始时间的从小到大排列
Arrays.sort(intervals,(o1,o2)->(o1[0]-o2[0]));
int res=0;
for(int[] time:intervals){
//其中0代表开始时间,1代表结束时间,判读a会议和b会议能不能共存:a结束的时候(指的是队列的peek)b是否开始了(指的是time[0])
//a结束的时间a_start与b开始的时间b_end比大小,
//eg:a会议10点开始 b会议9点结束,a开始的时候b已经结束,所以不能共存要poll()丢出
while (!queue.isEmpty() && time[0] >= queue.peek()){
queue.poll();
}
//队列只保存每次的结束时间(小顶堆的目的就是为了找到最早结束的会议的时间)
queue.add(time[1]);
//最大的队列size就是最终要找到的会议室数量 参考最开始的思路
res=Math.max(res, queue.size());
}
return res;
}
}
(2)上车下车算法(摩尔投票法)
使用上车下车算法:
- 分别对开始时间和结束时间排序。
- 排序以后用两指针分别迭代两个数组。 使用计数器表示上车和下车的人数,start小的计数器+1,end小的计数器-1,分别表示上车数和下车人数。如果end和start的值一样,说明正好抵消,有人上车的同时有人下车。
- 需要记录车上某个时刻的最大值, 这个最大值就是需要的会议室的数量。
class Solution {
/**
看了题解以后,觉得自己很SB
使用上车下车算法:
1. 分别对开始时间和结束时间排序。
2. 排序以后用两指针分别迭代两个数组。 使用计数器表示上车和下车的人数,start小的计数器+1,end小的计数器-1,分别表示上车数和下车人数。如果end和start的值一样,说明正好抵消,有人上车的同时有人下车。
3. 需要记录车上某个时刻的最大值, 这个最大值就是需要的会议室的数量。
**/
public int minMeetingRooms(int[][] intervals) {
if(intervals == null || intervals.length == 0)
return 0;
int[] start = new int[intervals.length];
int[] end = new int[intervals.length];
for(int i = 0; i < intervals.length; i++) {
start[i] = intervals[i][0];
end[i] = intervals[i][1];
}
Arrays.sort(start);
Arrays.sort(end);
int p1 = 0, p2 =0;
int max = 0;
int count = 0;
//p1 是start的指针,p1到最后也就结束了
while(p1 < end.length) {
//会议开始在最近结束的会议之前,count + 1
if(start[p1] < end[p2]) {
count++;
p1++;
max = Math.max(max, count);
} else if (start[p1] > end[p2]) {
//会议开始在最近结束的会议之后,count + 1
count--;
p2++;
} else {
//会议同时开始和结束,直接抵消
p1++;
p2++;
}
}
return max;
}
}
3. 合并区间

(1)排序(List)
对所有的区间按照左端点升序排序,然后遍历。
- 如果当前遍历到的区间的左端点 > 结果集中最后一个区间的右端点,说明它们没有交集,此时把区间添加到结果集;
- 如果当前遍历到的区间的左端点 <= 结果集中最后一个区间的右端点,说明它们有交集,此时产生合并操作,即:对结果集中最后一个区间的右端点更新(取两个区间的最大值)。
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.Comparator;
import java.util.List;
import java.util.Stack;
public class Solution {
public int[][] merge(int[][] intervals) {
int len = intervals.length;
if (len < 2) {
return intervals;
}
// 按照起点排序
Arrays.sort(intervals, (o1,o2) -> o1[0] - o2[0]);
// 也可以使用 Stack,因为我们只关心结果集的最后一个区间
List<int[]> res = new ArrayList<>();
res.add(intervals[0]);
for (int i = 1; i < len; i++) {
int[] curInterval = intervals[i];
// 每次新遍历到的列表与当前结果集中的最后一个区间的末尾端点进行比较 res.get(res.size() - 1)[1]
//如果更大,则无交集
if (curInterval[0] > res.get(res.size() - 1)[1]) {
res.add(curInterval);
} else {
// 注意,这里应该取最大
res.get(res.size() - 1)[1] = Math.max(curInterval[1], res.get(res.size() - 1)[1]);
}
}
return res.toArray(new int[res.size()][]);
}
public static void main(String[] args) {
Solution solution = new Solution();
int[][] intervals = {{1, 3}, {2, 6}, {8, 10}, {15, 18}};
int[][] res = solution.merge(intervals);
for (int i = 0; i < res.length; i++) {
System.out.println(Arrays.toString(res[i]));
}
}
}
(2)排序(数组)
class Solution {
public int[][] merge(int[][] intervals) {
// 先按照区间起始位置排序
Arrays.sort(intervals, (v1, v2) -> v1[0] - v2[0]);
// 遍历区间
int[][] res = new int[intervals.length][2];
int idx = -1;
for (int[] interval: intervals) {
// 如果结果数组是空的,或者当前区间的起始位置 > 结果数组中最后区间的终止位置,
// 则不合并,直接将当前区间加入结果数组。
if (idx == -1 || interval[0] > res[idx][1]) {
res[++idx] = interval;
} else {
// 反之将当前区间合并至结果数组的最后区间
res[idx][1] = Math.max(res[idx][1], interval[1]);
}
}
return Arrays.copyOf(res, idx + 1);
}
}
4. 插入区间
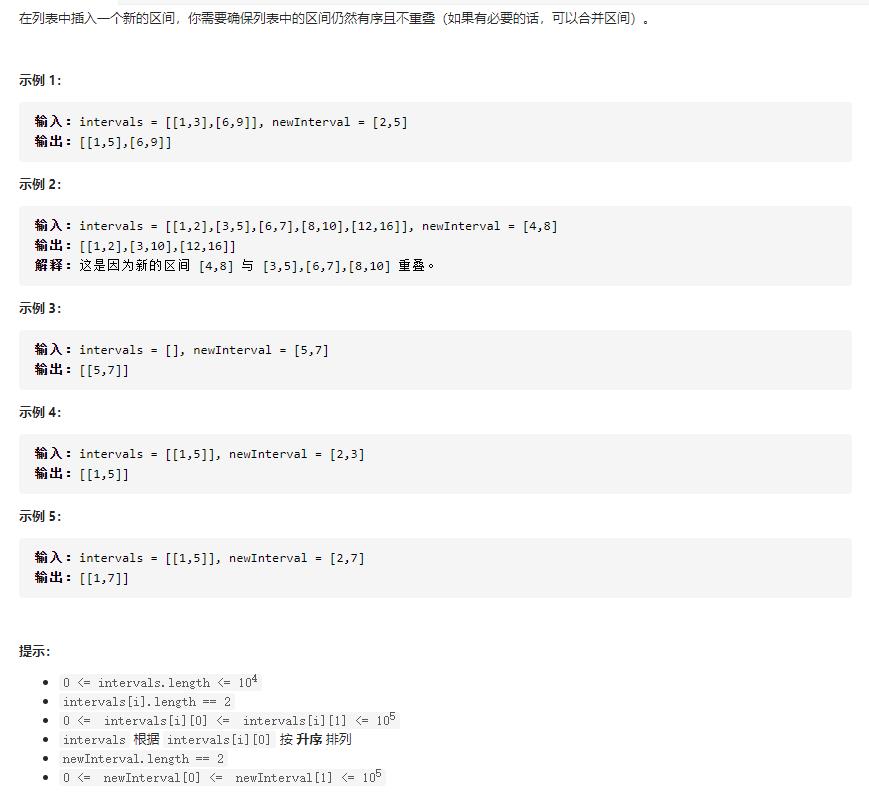
(1)模拟
-
首先将新区间左边且相离的区间加入结果集(遍历时,如果当前区间的结束位置小于新区间的开始位置,说明当前区间在新区间的左边且相离);
-
接着判断当前区间是否与新区间重叠,重叠的话就进行合并,直到遍历到当前区间在新区间的右边且相离,将最终合并后的新区间加入结果集;
-
最后将新区间右边且相离的区间加入结果集。
class Solution {
public int[][] insert(int[][] intervals, int[] newInterval) {
int[][] res = new int[intervals.length + 1][2];
int idx = 0;
// 遍历区间列表:
// 首先将新区间左边且相离的区间加入结果集
int i = 0;
while (i < intervals.length && intervals[i][1] < newInterval[0]) {
res[idx++] = intervals[i++];
}
// 接着判断当前区间是否与新区间重叠,重叠的话就进行合并,直到遍历到当前区间在新区间的右边且相离,
// 将最终合并后的新区间加入结果集
while (i < intervals.length && intervals[i][0] <= newInterval[1]) {
newInterval[0] = Math.min(intervals[i][0], newInterval[0]);
newInterval[1] = Math.max(intervals[i][1], newInterval[1]);
i++;
}
res[idx++] = newInterval;
// 最后将新区间右边且相离的区间加入结果集
while (i < intervals.length) {
res[idx++] = intervals[i++];
}
return Arrays.copyOf(res, idx);
}
}
(2)左右不重合的添加到集合list中,中间合并添加到集合list中
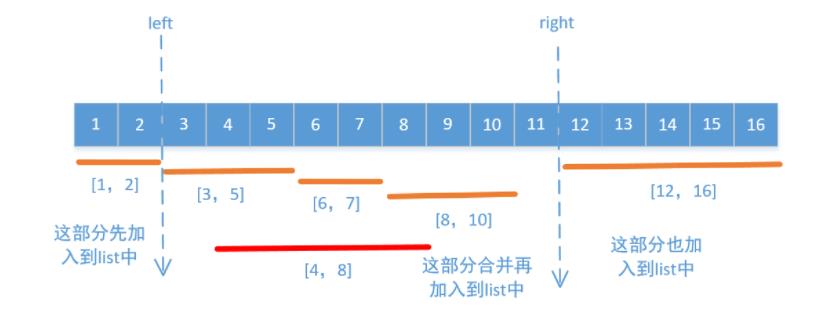
这里我们人为把数组分为3部分,左边不重合的添加到集合list中,右边不重合的也添加到集合list中,然后再合并中间的,这里以示例2为例画个图看一下
public int[][] insert(int[][] intervals, int[] newInterval) {
//边界条件判断
if (intervals.length == 0)
return new int[][]{newInterval};
List<int[]> resList = new ArrayList<>();
//一个从左边开始找不重合的
int left = 0;
//一个从右边开始找不重合的
int right = intervals.length - 1;
//左边不重合的添加到list中
while (left < intervals.length && intervals[left][1] < newInterval[0]) {
resList.add(intervals[left++]);
}
//右边不重合的添加到list中
while (right >= 0 && intervals[right][0] > newInterval[1]) {
resList.add(left, intervals[right--]);
}
//下面一大坨是合并中间重合的,注意一些边界条件的判断
int[] newArr = new int[2];
newArr[0] = left >= intervals.length ? newInterval[0] : Math.min(intervals[left][0], newInterval[0]);
newArr[1] = right < 0 ? newInterval[1] : Math.max(intervals[right][1], newInterval[1]);
resList.add(left, newArr);
//这一大坨是把list转二维数组
int[][] resArr = new int[resList.size()][2];
for (int i = 0; i < resList.size(); i++) {
resArr[i] = resList.get(i);
}
return resArr;
}
(2)从左边开始,逐步合并
- 第一种方式是先把两边不重合的添加到集合list中之后在合并中间的。
- 这里还可以从左边开始把不重合的(如果有不重合的)添加到集合list中
- 如果遇到重合的就找出重合的范围然后再添加到集合中,最后再把后面不重合的(如果有)添加到集合list中。
public int[][] insert(int[][] intervals, int[] newInterval) {
List<int[]> resList = new ArrayList<>();
int i = 0;
//先把前面不重合的添加到list中
while (i < intervals.length && intervals[i][1] < newInterval[0])
resList.add(intervals[i++]);
int mergeStar = newInterval[0];
int mergeEnd = newInterval[1];
//前面不重合的都添加到集合list中了,从这里开始就出现重合了,我们要找到重合的开始和结束值
while (i < intervals.length && intervals[i][0] <= newInterval[1]) {
mergeStar = Math.min(mergeStar, intervals[i]