《数据结构与算法》第一篇

Posted 2021-09-24 花嵩

文章目录

• 前言：
• 算法高效性的2个主要指标：时间复杂度，空间复杂度
• • 时间复杂度（执行算法的时间成本）
  • • 序章：
    • 普通函数的时间复杂度
    • 递归函数的时间复杂度
  • 空间复杂度（执行算法的空间成本）：
  • • 普通函数的空间复杂度：
    • 递归函数的空间复杂度：
• 总结

前言：

• 博主新开了一个专栏《数据结构与算法》，望各位大佬，多多支持，非常感谢！

• 博主目前处于数据结构的入门阶段，博文有什么错误，望各位大佬 不吝赐教，非常感谢！

• 就像C生万物一样，数据结构与算法之间的是形影不离的，谈到数字节构必然要谈算法的。

算法高效性的2个主要指标：时间复杂度，空间复杂度

时间复杂度（执行算法的时间成本）

序章：

• 由于受运行环境和输入规则的影响，代码的绝对执行时间是不可预知的。但是我们却可以预估代码的基本执行操作执行次数T(N)，来预估代码执行时间。但是对与不同算法，以T(N1)=0.5N² +0.5N，T(N2)=100N为例，我们当如何比较呢？

• 为了解决时间分析问题，有了渐进时间复杂度

官方定义：

若存在函数f(N),使得当N趋于无穷大时，T(N)/f(N)的极限值是不为0的常数，则称f(N)是T(N)的同量级函数，记作：T(N)=0(f(N)), 0为算法的渐进时间复杂度，简称时间复杂度

因为渐进时间复杂度用大写0来表示，所以也称为大0 渐进法

• 时间复杂度表示法：大0表示法

规则：

• 如果运行时间是常数量级，则用常数1表示

• 只保留最影响执行次数的那一项

• 如果那一项存在，则省去哪一项前面的系数，因为当N很大时，系数已无关紧要。

普通函数的时间复杂度

EXP1:

/ 请计算一下Func1基本操作执行了多少次？
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N ; ++ i)
{
for (int j = 0; j < N ; ++ j)
{
++count;
}
}
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\\n", count);
}

• F(N)=N² + 2*N +10

F(N)
F(10)	130
F(100)	10210
F(1000)	1002010
…

• 当N趋于无穷大时，对于F(N)可以说只有N² 在影响结果。因此这也就是大0渐进的原因

• 但是对与一个算法，以二分查找为例，我们必须考虑不同的情况

最坏情况	任意输入规模的最大运行次数(上界），二分查找要找到最后
平均情况	任意输入规模的期望运行次数，二分查找要找到中间
最好情况	任意输入规模的最小运行次数(下界)，二分查找第一次就找到

• 在实际中一般情况关注的是算法的最坏运行情况，就像等人一样，要做好等待时间超过心里预期的情况。

• 因此fun1的时间复杂度是：0(N² )

EXP2:

// 计算Func3的时间复杂度？
void Func3(int N, int M)
{
int count = 0;
for (int k = 0; k < M; ++ k)
{
++count;
}
for (int k = 0; k < N ; ++ k)
{
++count;
}
printf("%d\\n", count);
}

• 时间复杂度：0(M+N);

M于N互不相关，因此独立计算执行次数

EXP3:

// 计算BubbleSort（冒泡法）的时间复杂度？
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t i = 0; i <n-1; i++)
{
int exchange = 0;
for (size_t j = 0; j < end-1-i; j++)
{
if (a[j] > a[j+1])
{
Swap(&a[j], &a[j+1]);
exchange = 1;
}
}
if (exchange == 0)//如果没发生交换，说明数组已经是按从小到大排好序了
break;
}

• 时间复杂度：0(N²)

EXP4:

// 计算BinarySearch(二分查找)的时间复杂度？
//默认数组从小到大排好序了
int BinarySearch(int* a, int n, int x)
{
assert(a);
int left= 0;
int right= n-1;
while (left <= right)
{
int mid =(left+right)/2;
if (a[mid] < x)
{
    left = mid+1;
}
else if (a[mid] > x)
{
    right= mid-1;
}  
  else
  { 
      return mid;
  }
}
return -1;
}

• 时间复杂度：0(log2ⁿ)

递归函数的时间复杂度

递归函数的时间复杂度，我们看的是其递归次数也就是深度。

EXP1:

long long Factorial(size_t N)//阶层
{
return N < 2 ? N : Factorial(N-1)*N;
}

• 递归深度为：N，因此时间复杂度：0（N）

EXP2：

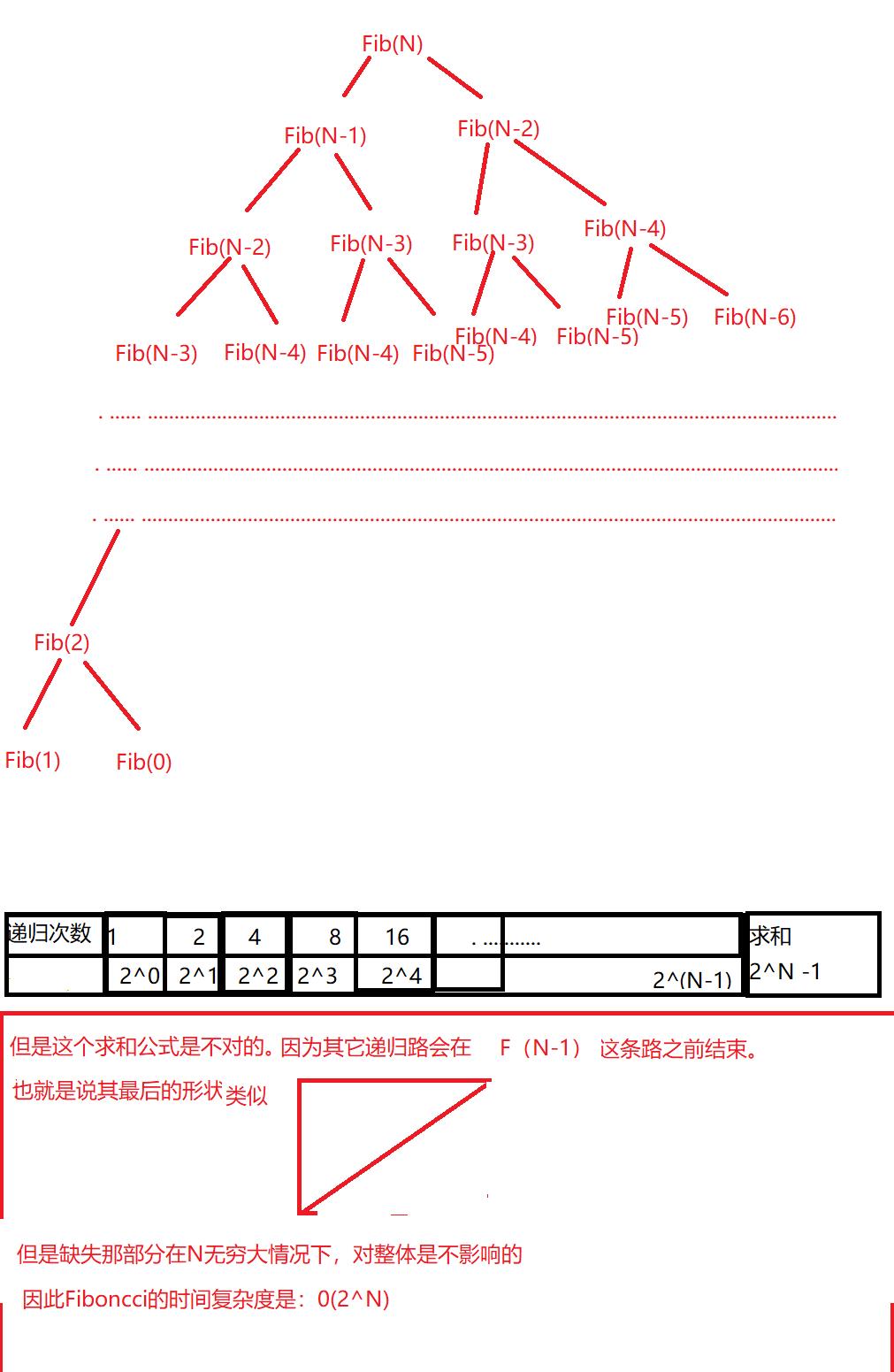
long long Fibonacci(int N)
{

return N<2 ? N:Fiboncci(N-1)+Fiboncci(N-2)

}

时间复杂度：0(2^N)

空间复杂度（执行算法的空间成本）：

间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用 了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。空间复杂度计 算规则基本跟时间复杂度类似，也使用大O渐进表示法。

普通函数的空间复杂度：

EXP1:

void BubbleSort(int* a, int n)
{
assert(a);
for (size_t i = 0; i <n-1; i++)
{
int exchange = 0;
for (size_t j = 0; j < end-1-i; j++)
{
if (a[j] > a[j+1])
{
Swap(&a[j], &a[j+1]);
exchange = 1;
}
}
if (exchange == 0)//如果没发生交换，说明数组已经是按从小到大排好序了
break;
}

• 空间复杂度：因为临时变量（形参也算）是常数个。因此空间复杂度：0（1）

EXP2：

/ 计算Fibonacci的空间复杂度？
long long* Fibonacci(size_t n)
{
    if(n==0)
         return NULL;
    long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));
    fibArray[0] = 0;
    fibArray[1] = 1;
    for (int i = 2; i <= n ; ++i)
    {
          fibArray[i ] = fibArray[ i - 1] + fibArray [i - 2];
    }
    return fibArray ;
}

空间复杂度：因为临时开辟了N个空间因此空间复杂度是0（N）

递归函数的空间复杂度：

EXP1:

// 计算阶乘递归Factorial的空间复杂度？
long long Factorial(size_t N)
{
return N < 2 ? N : Factorial(N-1)*N;
}

• 因为每次递归了N次，因此函数栈帧了N次，但是每次都是常数个变量。因此空间复杂度为：0（N）

EXP2：

long long Fibonacci(int N)
{

return N<2 ? N:Fiboncci(N-1)+Fiboncci(N-2)

}

• 递归是树形，因此空间复杂度是0（N）

总结

• 博主目前处于《数据结构》的入门阶段，因此博文有什么错误，请各位大佬指出，非常感谢！