二叉搜索树的思想，以及增删查改的实现

Posted 2021-09-24 有裂痕的石头

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了二叉搜索树的思想，以及增删查改的实现相关的知识，希望对你有一定的参考价值。

搜索树的概念

二叉搜索树又被称为排序树，它或者是一颗空树，或者是一棵具有以下性质的二叉树：

若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树
下图就是一棵二叉搜索树，可以对应上面性质加深理解：

查找操作

实现思想：

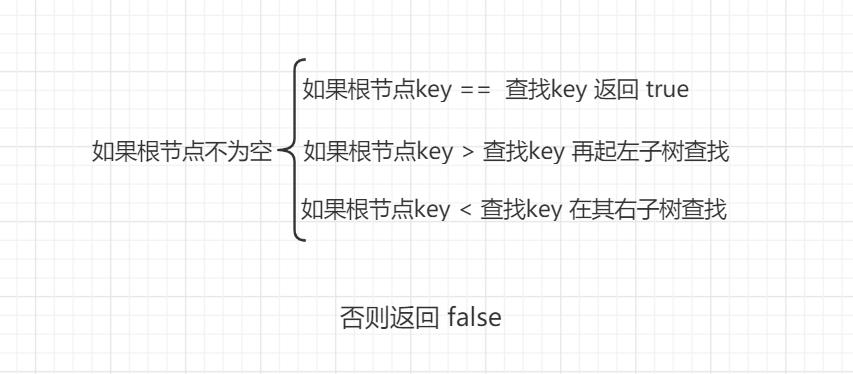
实现代码：

// O(树的高度)
 public boolean find(int key) {
        Node current = root;
        while (current != null) {
            if (key == current.key) {
                return true;
            } else if (key < current.key) {
                current = current.left;
            } else {
                current = current.right;
            }
        }

        return false;
    }

插入操作

实现思想：

如果树为空树，即根 == null，直接插入
如果不时空树，按照查找逻辑确定插入位置，插入新节点，这里需要引入两个变量

实现代码：

// O(树的高度)
 public void insert(int key) {
        if (root == null) {
            root = new Node(key);
            return;
        }
        Node parent = null;
        Node current = root;
        while (current != null) {
            if (key == current.key) {
                throw new RuntimeException("BST 中不允许重复的 key: " + key);
            } else if (key < current.key) {
                parent = current;
                current = current.left;
            } else {
                parent = current;
                current = current.right;
            }
        }

        // 1. 把关键字装入结点中
        Node node = new Node(key);
        if (key < parent.key) {
            parent.left = node;
        } else {
            parent.right = node;
        }
    }

删除操作

设待删除节点为cur，待删除节点的双亲节点为parent
有以下三种情况：

实现代码：

  // O(树的高度)
    public boolean remove(int key) {
        Node parent = null;
        Node current = root;
        while (current != null) {
            if (key == current.key) {
                // 删除 current 中的 key
                removeNode(parent, current);
                return true;
            } else if (key < current.key) {
                parent = current;
                current = current.left;
            } else {
                parent = current;
                current = current.right;
            }
        }

        return false;
    }

    // O(1)
    private void removeNode(Node parent, Node current) {
        if (current.left == null) {
            if (current == root) {
                root = current.right;
            } else if (current == parent.left) {
                parent.left = current.right;
            } else {
                parent.right = current.right;
            }
        } else if (current.right == null) {
            if (current == root) {
                root = current.left;
            } else if (current == parent.left) {
                parent.left = current.left;
            } else {
                parent.right = current.left;
            }
        } else {
            Node goat = current.right;
            Node goatParent = current;
            while (goat.left != null) {
                goatParent = goat;
                goat = goat.left;
            }

            // 替换
            current.key = goat.key;
            // 删除 goat 结点
            if (goatParent == current) {
                goatParent.right = goat.right;
            } else {
                goatParent.left = goat.right;
            }
        }
    }