二叉树之结点相关操作
Posted 变秃变强 呀
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二叉树之结点相关操作相关的知识,希望对你有一定的参考价值。
结点的个数
求解树的结点总数时,可以将问题拆解成子问题:
1.若为空,则结点个数为0。
2.若不为空,则结点个数 = 左子树结点个数 + 右子树结点个数 + 1(自己)。
代码实现
int BinaryTreeSize(BT* root)
{
//结点个数 = 左子树的结点个数 + 右子树的结点个数 + 自己
return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
图解递归
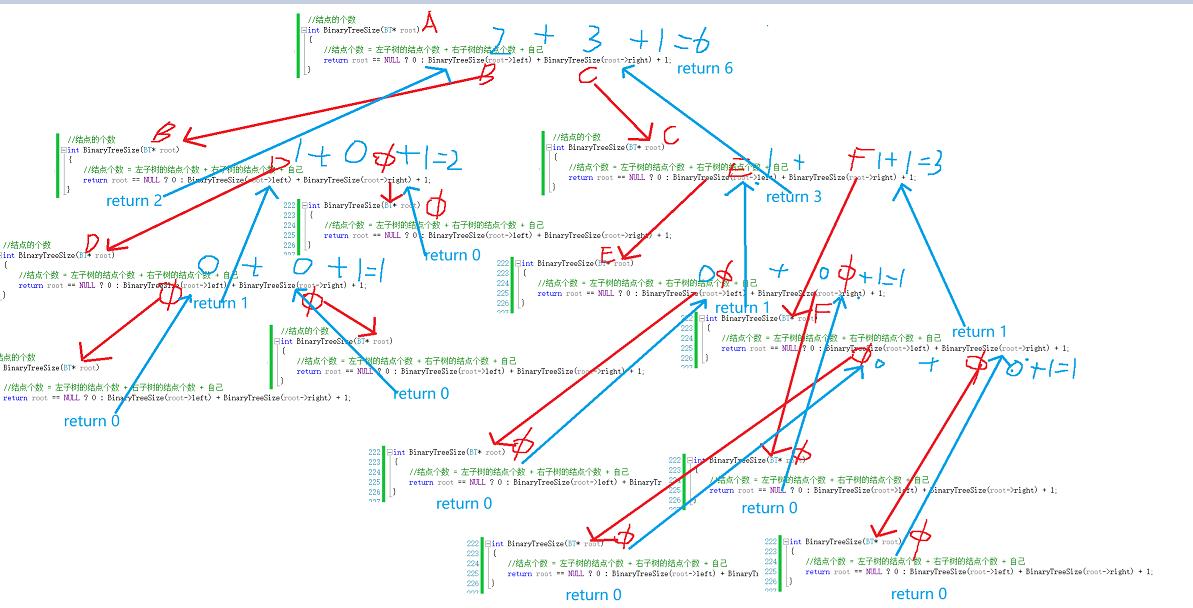
当你自己画完其递归过程后,你会发现其实它就相当于后序遍历,BinaryTreeSize(root->left)相当于左子树,BinaryTreeSize(root->right)相当于右子树,而最后加的那个1,其实就是根结点。
叶子结点的个数
子问题拆解:
1.若为空,则叶子结点个数为0。
2.若结点的左指针和右指针均为空,则叶子结点个数为1。
3.除上述两种情况外,说明该树存在子树,其叶子结点个数 = 左子树的叶子结点个数 + 右子树的叶子结点个数。
代码实现
int BinaryTreeLeafSize(BT* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL&&root->right == NULL)
{
return 1;
}
return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
图解递归
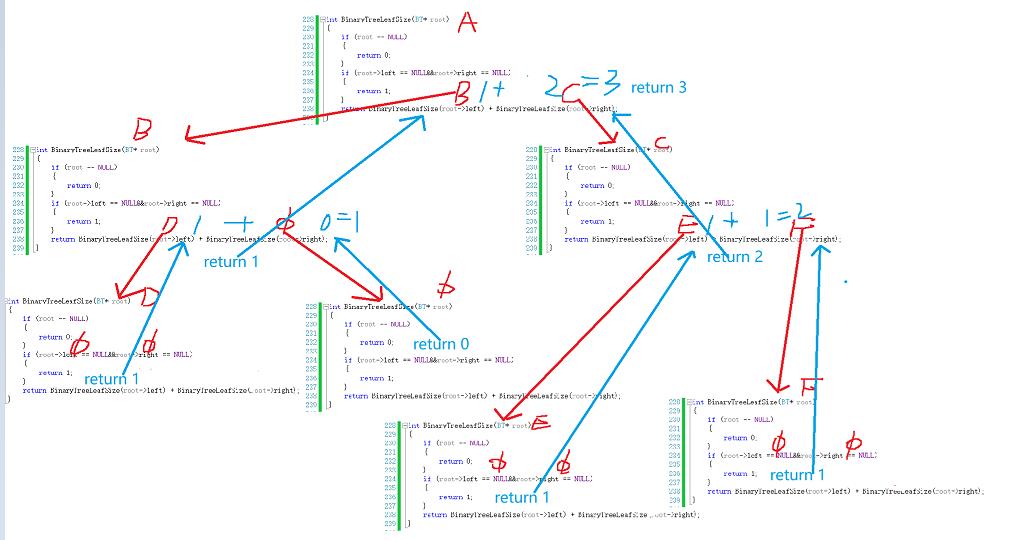
这里要注意,root==NULL这个必须写在最前面,不能写在后面,因为万一是空树的情况,那样你root->left访问就会出问题。
第k层结点的个数
思路:
相对于根结点的第k层结点的个数 = 相对于以其左孩子为根的第k-1层结点的个数 + 相对于以其右孩子为根的第k-1层结点的个数

代码实现
int BinaryKlevelSize(BT* root,int k)
{
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return BinaryKlevelSize(root->left, k - 1) + BinaryTreeKLevelSize(root->right, k - 1);
}
图解递归
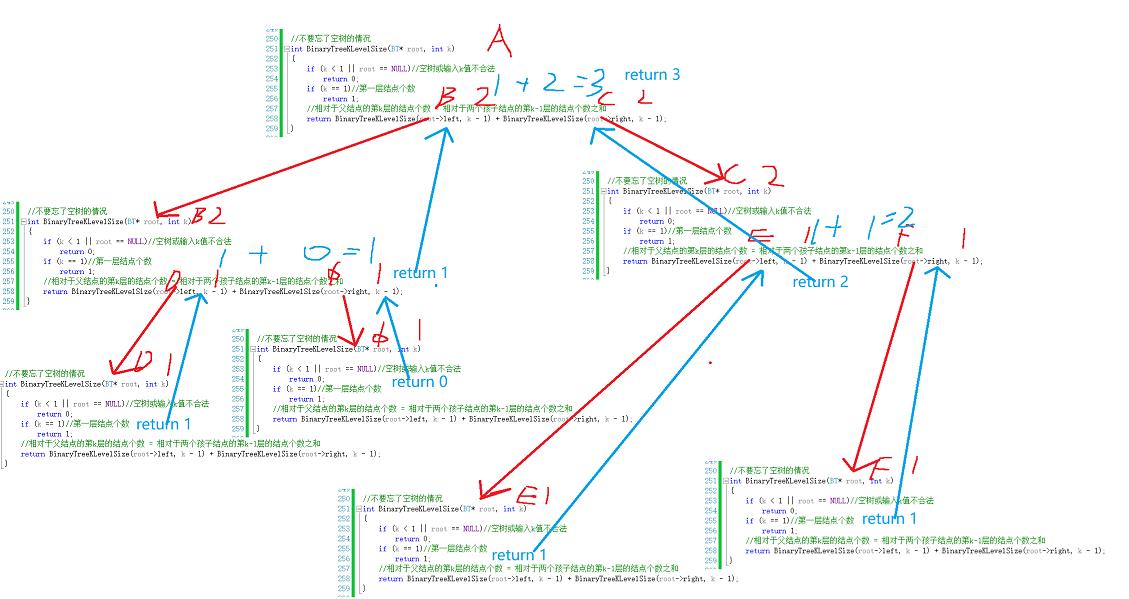
值为x的结点
子问题:
1.先判断根结点是否是目标结点。
2.再去左子树中寻找。
3.最后去右子树中寻找。
代码实现
BT* BinaryTreeFind(BT* root,BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->x == x)
{
return root;
}
struct BinaryNode* ansleft = BinaryTreeFind(root->left, x);
if (ansleft)
{
return ansleft;
}
struct BinaryNode* ansright = BinaryTreeFind(root->right, x);
if (ansright)
{
return ansright;
}
return NULL;
}
这块代码其实是很容易写出一个编译器的Bug的,读者不防试试把前面两个if的{}去掉试试看,此时你就会发现一个编译器的Bug。
关于这个问题读者们有兴趣的话可以去看看我写的这篇文章:💥不经意之间的Bug(1):有些编译器可能在某些情况下无法识别typedef定义的标识符
图解递归
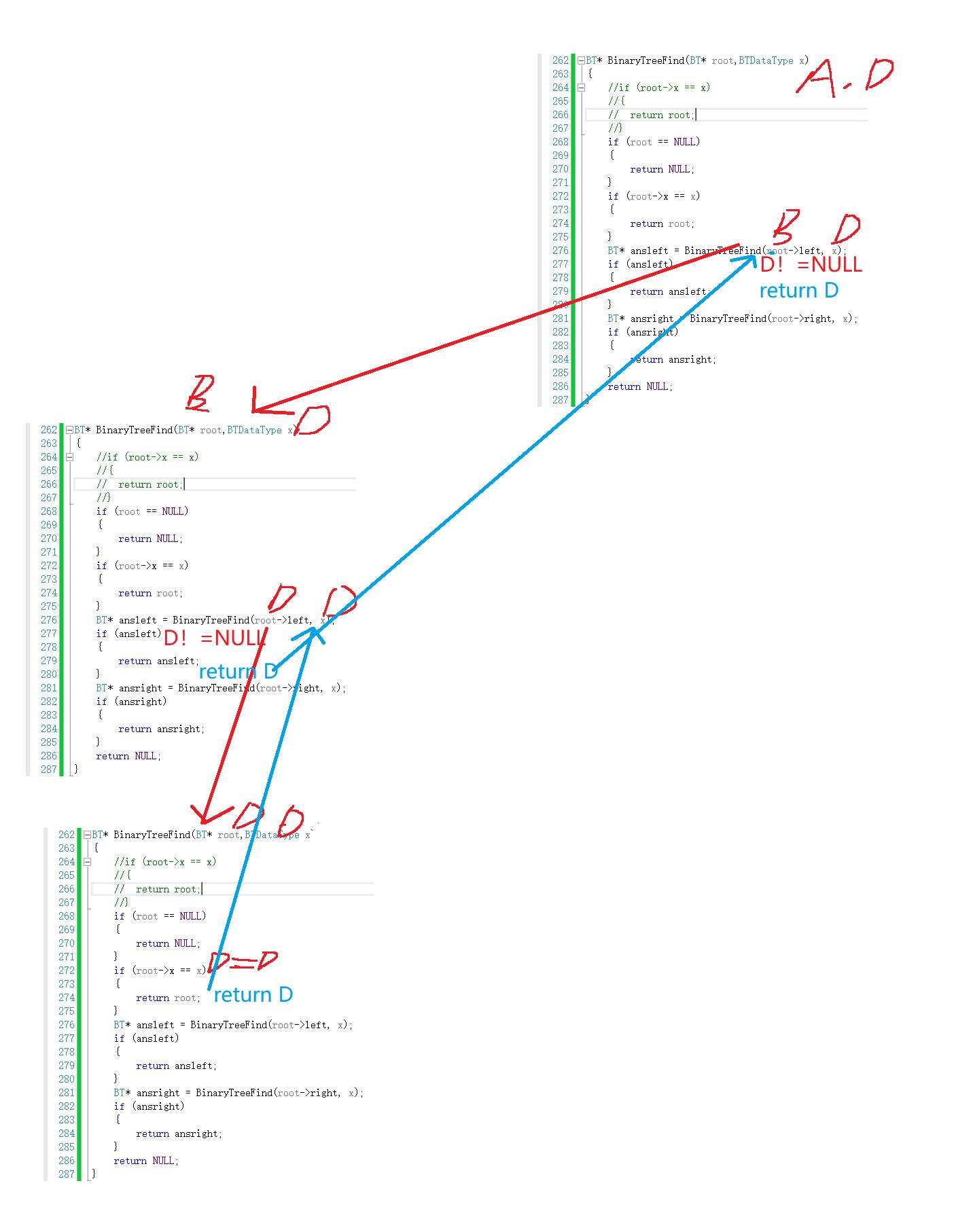
以上是关于二叉树之结点相关操作的主要内容,如果未能解决你的问题,请参考以下文章