[JavaScript 刷题] 数据结构 - 链表(Linked List)

Posted 2021-09-23 GoldenaArcher

[javascript 刷题] 数据结构 - 链表(Linked List)

链表是一种不需要占据连续物理空间去存储数据的有序结构。

它的结构由一个个的 结点(node) 组成，每个节点包含着当前存储的数据，以及下一个节点的地址，如：

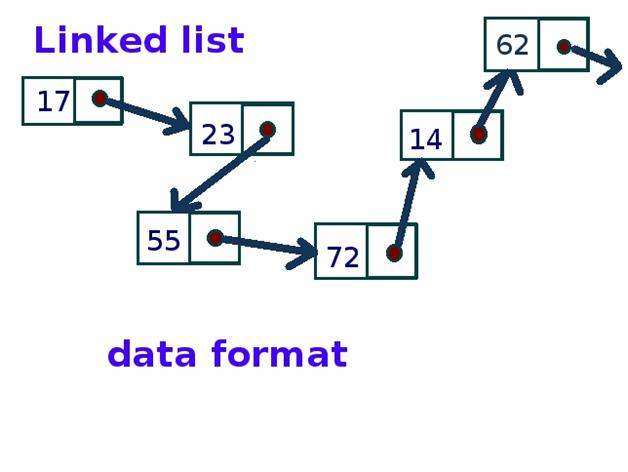
图像资料来源于: https://image.cha138.com/20210923/0bd564590b2c456f9276a0533af9ecfd.jpg/

链表的结构对于底层的实践来说非常重要，一来它可以有效的使用碎片空间去存储数据，二来对于需要经常重写的数据，在链表中进行增删的效率远远比数组的效率要高。

对于数组来说，在下标 $n$ 增加/删除一个数据，意味需要将 $n+1,...,arr.length-1$ 的数据全都向后移动一个下标，时间复杂度为 $O(n)$。对于数据量很大的情况下来说，在数组中进行随机的增删，无疑是一个很大的压力:

可以看到，代码都是相同的情况下，在尾部增加数据(使用 push) 耗时只有 在头部增加数据(使用 unshift) 的 1/10。

对于链表而言，只需要将 $n$ 的下一个地址指向新增数据的地址，并且将新增数据的下一个地址指向 $n+1$ 数据的地址，就能完成操作，因此对于链表来说，增删的时间复杂度为 $O(1)$。

这是链表的优点，但是链表的缺点就在于它是一个动态的数据结构，没有办法直接根据索引去获得链表中的值。因此在链表中要获取某个值的操作只能去遍历整个链表，时间复杂度为 $O(n)$。对比数组可以直接通过索引去获取值，时间复杂度为 $O(1)$ 的情况，一般使用的先决条件为：

• 需要大量 增删 数据时，使用链表
• 需要大量 读取 数据时，使用数组

基础实现及测试完整代码的下载地址：LinkedList 功能

链表的实现

节点的实现：

class Node {
  value = null;
  next = undefined;

  constructor(value, next = undefined) {
    this.value = value;
    this.next = next;
  }
}

节点是一个能够保存对应的值，以及下一个元素地址的数据结构，因此在实现的时候设置两个属性即可。

链表的实现：

链表的类型稍微复杂，分别依据以下的函数进行实现：

• addFirst

  在头部添加

  这个理解起来还是比较简单的，相当于直接新建一个新的节点 newHead，将原本的 Head 存储为 newHead.next 即可。

  实现为：

  addFirst(value) {
    const newHead = value instanceof Node ? value : new Node(value);
  
    if (this.count === 0) {
      this.head = newHead;
    } else {
      newHead.next = this.head;
      this.head = newHead;
    }
    this.count++;
  }
  

• addLast

  在尾部添加

  这个逻辑也比较简单，循环找到最后一个节点，即，满足 tail.next === null 这个条件的 Node。新建一个 newTail，完成 tail.next 指向 newTail 即可。

  实现如下：

  addLast(value) {
    // 判断传进来的value是不是节点，是的话直接将 next 指向该节点，不然就创建一个新的节点
    const newTail = value instanceof Node ? value : new Node(value);
  
    if (this.count === 0) {
      this.head = newTail;
    } else {
      // 找到尾部的数据，再进行 append 的操作
      let curr = this.head;
      while (curr.next !== null) {
        curr = curr.next;
      }
      curr.next = newTail;
    }
    this.count++;
  }
  

• addAt(value, index)

  在中间添加

  这部分我做的逻辑就是，当传进来的 index <= 0 时，调用 addFirst；当 index > 链表长度时，调用 addLast。

  其他情况，则调用 getIndex(index)去获取 指定索引的前一位 prev，将 prev.next 指向新创建的节点，再将新创建的节点的 next 指向 prev.next.next。

  如，本来的链表结构如下：

  此时需要在索引 2 添加新的节点 Node(3)，使得链表结构成为 1 --> 2 --> 3 --> 4 --> 5。那么需要做的就是断开 2 --> 4 之间的联系，更改 next 的指向，将 2.next --> 3，3.next --> 4，如：

  实现如下：

  addAtIndex(value, index) {
    const node = value instanceof Node ? value : new Node(value);
  
    if (index <= 0) {
      this.addFirst(value);
    } else if (index > this.count) {
      this.addLast(value);
    } else {
      const prev = this.getIndex(index - 1);
      const tempCurr = prev.next;
      prev.next = node;
      node.next = tempCurr;
      this.count++;
    }
  }
  

• getIndex(index)

  通过索引获取节点，先实现这个函数再去实现 addAt(value, index) 会简单很多。

  这里其实依旧是一个 for 循环，循环条件就是当 $[0,...,index)$ 或 $[1,...,index]$，取决于如何对循环体进行实现的。

  实现如下：

    /**
   *
   * @param {Number} index
   * @return {Node} Node founde
   */
  getIndex(index) {
    if (index > this.count || index < 0 || this.count === 0) return undefined;
  
    let curr = this.head;
    for (let i = 0; i < index; i++) {
      curr = curr.next;
    }
  
    return curr;
  }
  

• removeAtIndex

  删除指定索引的节点

  这个实现方法和 getIndex 的逻辑正好相反，如果原本的结构如下：

  以上是关于[JavaScript 刷题] 数据结构 - 链表(Linked List)的主要内容，如果未能解决你的问题，请参考以下文章

  [JavaScript 刷题] 链表 - 相交链表, leetcode 160

  [JavaScript 刷题] 链表 - 相交链表, leetcode 160

  [JavaScript 刷题] 链表 - 反转链表, leetcode 206

  [JavaScript 刷题] 链表 - 反转链表, leetcode 206

  [JavaScript 刷题] 链表 - 合并两个有序链表, leetcode 21

  [JavaScript 刷题] 链表 - 链表的中间结点, leetcode 876