论文阅读|struc2vec: Learning Node Representations from Structural Identity
Posted 白鳯
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了论文阅读|struc2vec: Learning Node Representations from Structural Identity相关的知识，希望对你有一定的参考价值。
论文阅读|struc2vec: Learning Node Representations from Structural Identity
文章目录
Abstract
struc2vec 使用层次结构来衡量不同尺度的节点相似性，并构建一个多层图来编码结构相似性并为节点生成结构上下文。
Introduction
确定节点结构身份的最常见的实用方法是基于距离或递归。 在前者中，利用节点邻域的距离函数来测量所有节点对之间的距离，然后执行聚类或匹配以将节点放入等效类 。 后者中，构建关于相邻节点的递归，然后迭代展开直到收敛，最终值用于确定等效类 。
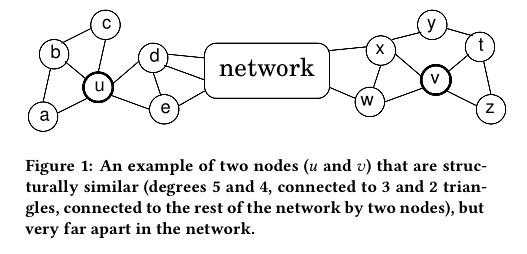
领域相似的结点具有结构相似性，但距离比较远的这样的结点就不具有相似性。如上图结点u和v。
DeepWalk和Node2vec在结构等效性任务中表现很差，因为现在的 网络都具有很强的同质性。
struc2vec的具体过程如下：
- 独立于节点和边属性以及它们在网络中的位置来评估节点之间的结构相似性。 因此，具有相似局部结构的两个节点将被视为独立于其邻域中的网络位置和节点标签。 我们的方法也不需要连接网络，并在不同的连接组件中识别结构相似的节点。
- 建立层次结构来衡量结构相似性，允许对结构相似性的含义逐渐提出更严格的概念。 特别是在层次结构的最底层，节点之间的结构相似度仅取决于它们的度数，而在层次结构的顶部，相似性取决于整个网络（从节点的角度来看）。
- 为节点生成随机上下文，这些节点是结构相似节点的序列，通过遍历多层图（而不是原始网络）的加权随机游走观察到。 因此，经常出现在相似上下文中的两个节点可能具有相似的结构。
对比算法：DeepWalk，Node2vec，RolX。
Related Work
DeepWalk：若两个节点的距离（即跳数）大于Skip-Gram的窗口大小，这种结构相似就被忽略了。
sub-graph2vec：使用邻居节点生成上下文，结构上非常相似（但未通过测试）且具有非重叠邻居的两个节点在空间上可能并不接近。
RolX：···
Strcu2vec
步骤：
- 确定不同邻域大小的图中每个顶点对之间的结构相似性。 这在节点之间结构相似性的度量中引入了层次结构，提供了更多信息来评估层次结构的每个级别的结构相似性。
- 构建一个加权的多层图，其中网络中的所有节点都存在于每一层中，每一层对应于衡量结构相似性的层次结构的一个级别。此外，每层内每个节点对之间的边权重与其结构相似性成反比。
- 使用多层图为每个节点生成上下文。特别是，使用有偏随机游走来生成节点序列。这些序列可能包括结构更相似的节点。
- 应用一种技术从节点序列给定的上下文中学习潜在表示，例如，SkipGram。
Measuring structural similarity
G=（V，E）， R k ( u ) 表 示 距 离 结 点 u 为 k 的 结 点 集 R_k(u)表示距离结点u为k的结点集 Rk(u)表示距离结点u为k的结点集
s ( S ) 表 示 结 点 集 合 S € V 的 有 序 度 数 序 列 s(S)表示结点集合S€V的有序度数序列 s(S)表示结点集合S€V的有序度数序列
通过比较节点u和v间距离为k的环路有序度序列，可以施加层次结构来测量结构相似性。特别地，当考虑它们的 k 跳邻域（距离小于或等于 k 的所有节点以及它们之间的所有边）时，让
f
k
(
u
,
v
)
f_k(u,v)
fk(u,v)表示 u 和 v 之间的结构距离。 特别地，定义：
f
k
(
u
,
v
)
=
f
k
−
1
(
u
,
v
)
+
g
(
s
(
R
k
(
u
)
)
,
s
(
R
k
(
v
)
)
)
,
k
≥
0
a
n
d
∣
R
k
(
u
)
∣
,
∣
R
k
(
v
)
∣
≥
0
;
f_k(u,v)=f_{k-1}(u,v)+g(s(R_k(u)),s(R_k(v))),k \\geq\\;0 \\quad and |R_k(u)|,|R_k(v)| \\geq\\ 0;
fk(u,v)=fk−1(u,v)+g(s(Rk(u)),s(Rk(v))),k≥0and∣Rk(u)∣,∣Rk(v)∣≥ 0;
其中
g
(
D
1
,
D
2
)
≥
0
g(D_1,D_2) \\geq\\; 0
g(D1,D2)≥0表示度数序列
D
1
,
D
2
D_1,D_2
D1,D2之间的距离，且
f
−
1
=
0
f_{-1}=0
f−1=0，
f
k
(
u
,
v
)
f_k(u,v)
fk(u,v)是递增的，当且仅当节点u和节点v之间距离不小于k。若u和v之间是同构的，并且u映射到v，则
f
k
−
1
(
u
,
v
)
=
0
f_{k-1}(u,v)=0
fk−1(u,v)=0。
采用DTW（Dynamic Time Warping）来测量两个有序度序列之间的距离，它可以很好地处理不同大小的序列并且松散地比较序列模式。使用它的原因是它惩罚了两个节点的度数都比较小时两者的差异。给定序列元素的距离函数
d
(
a
,
b
)
d(a,b)
d(a,b)，DTW匹配每个元素
a
∈
A
,
b
∈
B
a∈A,b∈B
a∈A,b∈B，使得匹配元素之间的距离总和最小化。采用以下距离函数：
d
(
a
,
b
)
=
m
a
x
(
a
,
b
)
m
i
n
(
a
,
b
)
−
1
d(a,b)=\\frac{max(a,b)}{min(a,b)}-1
d(a,b)=min(a,b)max(a,b)−1
当a=b时，则
d
(
a
,
b
)
=
0
d(a,b)=0
d(a,b)=0。
Constructing the context graph
构建层次带权图
k
∗
k^*
k∗表示网络的直径。每层
k
=
0
,
.
.
.
,
k
∗
k=0,...,k^*
k=0,...,k∗由一个带节点集V的加权无向图形成，一层中两个节点之间的边权重由下式给出：
w
k
(
u
,
v
)
=
e
−
f
k
(
u
,
v
)
,
k
=
0
,
.
.
.
,
k
∗
w_k(u,v)=e^{-f_k(u,v)},k=0,...,k^*
wk(u,v)=e−fk(u,v),k=0,...,k∗
第k层的节点u会连接到第k+1层和第k-1层。层间的边权重如下：
w
(
u
k
,
u
k
+
1
)
=
l
o
g
(
Γ
k
(
u
)
+
e
)
,
k
=
0
,
.
.
.
,
k
∗
−
1
w(u_k,u_{k+1})=log(\\Gamma_k(u)+e),k=0,...,k^*-1
w(uk,uk+1)=log(Γk(u)+e),k=0,...,k∗−1
w ( u k , u k − 1 ) = 1 , k = 1 , . . . , k ∗ w(u_k,u_{k-1})=1,k=1,...,k^* w(uk,uk−1)=1,k=1,...,k∗
其中
Γ
k
(
u
)
\\Gamma_k(u)
Γk(u)是与u相关且权重大于第k层中完整的平均边权重的边数，如下
Γ
k
(
u
)
=
∑
v
∈
V
1
(
w
k
(
u
,
v
)
>
w
k
‾
)
\\Gamma_k(u)=\\sum_{v∈V}1(w_k(u,v)>\\overline{w_k})
Γk(u)=v∈V∑1(wk(u,v)>wk)
其中
(
w
k
)
‾
=
∑
u
,
v
∈
(
V
2
)
w
k
(
u
,
v
)
/
(
V
2
)
\\overline{(w_k)}=\\sum_{u,v∈ \\begin{pmatrix}V \\\\ 2\\end{pmatrix}} w_k(u,v)/ \\begin{pmatrix} V \\\\ 2 \\end{pmatrix}
(wk)=∑以上是关于论文阅读|struc2vec: Learning Node Representations from Structural Identity的主要内容，如果未能解决你的问题，请参考以下文章
论文笔记｜深读struc2vec: Learning Node Representations from Structural Identity
论文阅读|DeepWalk: Online Learning of Social Representations
Deep Residual Learning for Image Recognition(ResNet)-论文阅读笔记
论文阅读之Improved Word Representation Learning with Sememes(2017)
论文阅读Single-Model Uncertainties for Deep Learning
A Generic Deep-Learning-Based Approach for Automated Surface Inspection-论文阅读笔记