85. 最大矩形

Posted 2021-09-22 炫云云

85. 最大矩形

给定一个仅包含 0 和 1 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例：

输入：

[
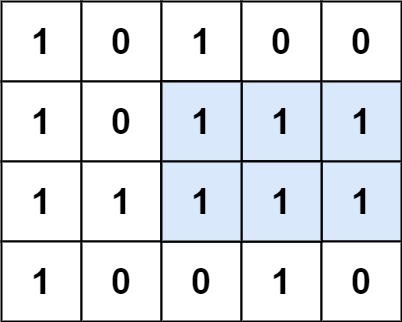
  ["1","0","1","0","0"],
  ["1","0","1","1","1"],
  ["1","1","1","1","1"],
  ["1","0","0","1","0"]
]

输出：6

我在 84. 柱状图中最大的矩形使用了多种方法来解决。 然而在这道题，我们仍然可以使用完全一样的思路去完成。 不熟悉的可以看下我的题解。本题解是基于那道题的题解来进行的。

拿题目给的例子来说：

[
  ["1","0","1","0","0"],
  ["1","0","1","1","1"],
  ["1","1","1","1","1"],
  ["1","0","0","1","0"]
]

我们逐行扫描得到 84. 柱状图中最大的矩形 中的 heights 数组：

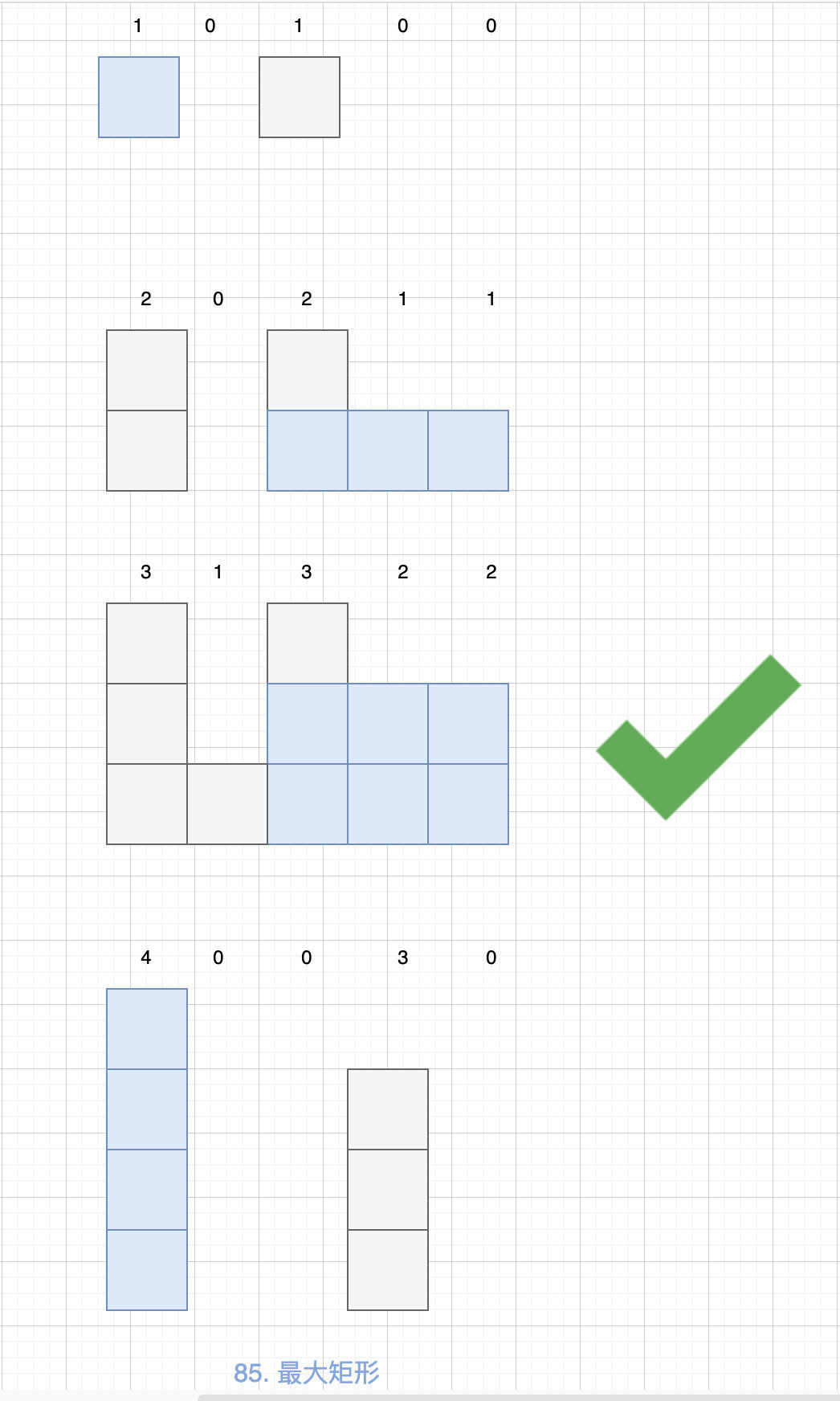
这样我们就可以使用84. 柱状图中最大的矩形 中的解法来进行了，这里我们使用单调栈来解。

下面的代码直接将 84 题的代码封装成 API 调用了。

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        stack = [-1] # 使用-1来代表开始位置,stack不可能为空，故无需stack判断 
        heights.append(0) # 加入哨兵值，便于原先heights中的最后位置的值弹出,因为需要比最后一个值小的值，才能把最后一个值卡在中间计算面积
        mxarea = 0
        for i, height in enumerate(heights):
            while heights[stack[-1]] > height:
                #当前值比栈顶的值小的时候，相当于两个比栈顶小的值把栈顶位置的数卡在中间，比如3,5，6，2，栈顶数为6
                #此时可以计算栈顶6围成的矩形面积
                area = heights[stack.pop()]*(i - stack[-1] - 1 )  
                if area>mxarea:
                    mxarea = area
            stack.append(i) #栈里面后面比前面大的时候才压入，相当于顺序压入
        return mxarea
    
    def maximalRectangle(self, matrix: List[List[str]]) -> int:
        m = len(matrix)
        if m == 0: return 0
        n = len(matrix[0])
        heights = [0] * n
        ans = 0
        for i in range(m):
            for j in range(n):
                if matrix[i][j] == "0":
                    heights[j] = 0
                else:
                    heights[j] += 1
            area = self.largestRectangleArea(heights)
            if area>ans:
                    ans = area
        return ans

参考

力扣（LeetCode） (leetcode-cn.com)