84. 柱状图中最大的矩形

Posted 2021-09-22 炫云云

84. 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

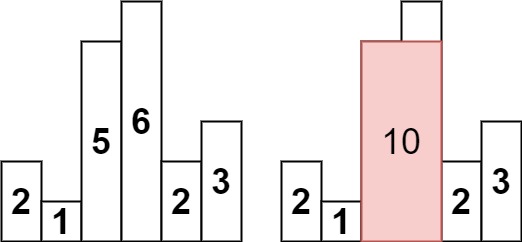
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

前言

我们需要在柱状图中找出最大的矩形，因此我们可以考虑枚举矩形的宽和高，其中「宽」表示矩形贴着柱状图底边的宽度，「高」表示矩形在柱状图上的高度。

如果我们枚举「宽」，我们可以使用两重循环枚举矩形的左右边界以固定宽度 $w$，此时矩形的高度 $h$，就是所有包含在内的柱子的「最小高度」，对应的面积为 $w\ast h$ ，而矩形的面积等于（右端点坐标 - 左端点坐标 + 1) * 最小的高度 。下面给出了这种方法的 代码。

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        n = len(heights)
        ans = 0
        # 枚举左边界
        for left in range(0,n):
            minHeight = float('inf')

            # 枚举右边界
            for right in range(left,n):
                # 确定高度
                minHeight = min(minHeight,heights[right])
                # 计算面积
                ans = max(ans, (right - left+1)*minHeight)

        return ans

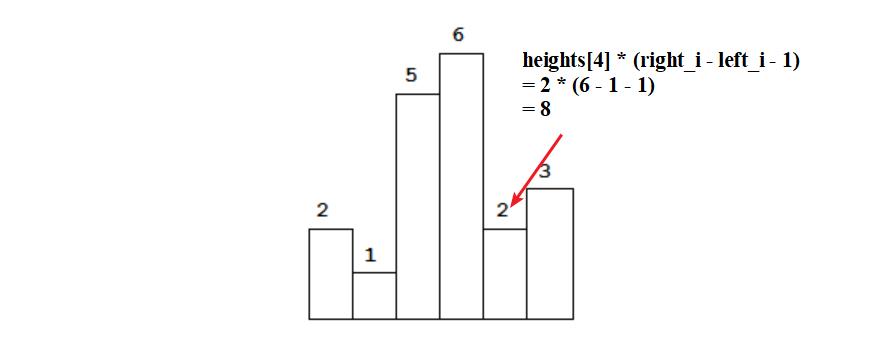
如果我们枚举「高」，对于每一个 $i$，我们计算出其左边第一个高度小于它的索引 $left$，同样地，计算出右边第一个高度小于它的索引 $right$。那么以 $i$ 为最低点能够构成的面积就是(right-left -1) * heights[i]。 这种算法毫无疑问也是正确的。 - 如下图所示：

我们证明一下，假设 $f(i)$ 表示求以 $i$ 为最低点的情况下，所能形成的最大矩阵面积。那么原问题转化为max(f(0), f(1), f(2), ..., f(n - 1))。

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        n = len(heights)
        ans = 0

        for mid in range(0,n):
            # 枚举高
            height = heights[mid]
            left = mid -1
            right = mid +1
            # 确定左右边界
            while left  >=0 and heights[left] >= height:
                left -=1
            while right<n and heights[right] >= height:
                right +=1
            ans = max(ans , (right-left -1) *height)
        return ans

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        n = len(heights)
        left, right = [0] * n, [0] * n

        for i in range(n):
            l = i -1
            while l >=0 and heights[l] >= heights[i]:
                l -=1
            left[i] = l  
        
        for i in range(n - 1, -1, -1):
            r  = i +1
            while r<n and heights[r] >= heights[i]:
                r +=1
            right[i] = r

        ans = max((right[i] - left[i] - 1) * heights[i] for i in range(n)) if n > 0 else 0
        return ans

复杂度分析

• 时间复杂度：$O(N^2)$
• 空间复杂度：$O(N)$

可以发现，这两种暴力方法的时间复杂度均为 $O(N^2)$ ，会超出时间限制，我们必须要进行优化。考虑到枚举「宽」的方法使用了两重循环，本身就已经需要 $O(N^2)$ 的时间复杂度，不容易优化，因此我们可以考虑优化只使用了一重循环的枚举「高」的方法。

单调栈

那么我们先来看看如何求出一根柱子的左侧且最近的小于其高度的柱子。

当我们枚举到第 $i$ 根柱子时，栈中存放了 $j_0,j_1,\cdots ,j_s$, 如果第 $i$ 根柱子左侧且最近的小于其高度的柱子为 $j_i$, 那么必然有
$$\mathrm{height}\left[j_0\right]<\mathrm{height}\left[j_1\right]<\cdots <\mathrm{height}\left[j_i\right]<\mathrm{height}[i]\le \mathrm{height}\left[j_{i+1}\right]<\cdots <\mathrm{height}\left[j_s\right]$$
由于栈中的 $j$ 值均小于 $i$, 那么所有高 度大于等于 height $[i]$ 的 $j$ 都不会作为答案, 需要从栈中移除。而我们发现，这些被移除的 $j$ 值恰好就是
$$j_{i+1},\cdots ,j_s$$
这样我们在枚举到第 $i$ 根柱子的时候，就可以先把所有高度大于等于 height $[i]$ 的 $j$ 值全部移除, 剩下的 $j$ 值中高度最高的即为答案。在这之后，我们将 $i$ 放入栈中，开始接下来的枚举。

• 栈中存放了 $j$ 值。从栈底到栈顶, $j$ 的值严格单调递增, 同时对应的高度值也严格单调递增;
• 当我们枚举到第 $i$ 根柱子时，我们从栈顶不断地移除 height $[j]\ge$ height $[i]$ 的 $j$ 值。在移除完毕 后, 栈顶的 $j$ 值就一定满足 height $[j]<$ height $[i]$, 此时 $j$ 就是 $i$ 左侧且最近的小于其高度的柱 子。
• 这里会有一种特殊情况。如果我们移除了栈中所有的 $j$ 值，那就说明 $i$ 左侧所有柱子的 高度都大于 $height[i]$, 那么我们可以认为 $i$ 左侧且最近的小于其高度的柱子在位置 $j=$ $-1$ ， 它是一根「虚拟」的、高度无限低的柱子。这样的定义不会对我们的答宋产生任何 的影响，我们也称这根「虚拟」的柱子为「哨兵」。
• 我们再将 $i$ 放入栈顶。

栈中存放的元素具有单调性，这就是经典的数据结构「单调栈」了。

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        n = len(heights)
        left, right = [0] * n, [0] * n

        left_i_stack = list() # 左边第一个小于其高度柱子下标
        for i in range(n):
            while left_i_stack and heights[left_i_stack[-1]] >= heights[i]:
                left_i_stack.pop() # 左边大于其高度，出栈
            left[i] = left_i_stack[-1] if left_i_stack else -1 # -1为最左边 ，
            left_i_stack.append(i) # 左边小于其高度
        
        right_i_stack = list() # 右边第一个小于其高度柱子下标
        for i in range(n - 1, -1, -1):
            while right_i_stack and heights[right_i_stack[-1]] >= heights[i]:
                right_i_stack.pop() # 右边大于其高度，出栈
            right[i] = right_i_stack[-1] if right_i_stack else n # n为最右边 ，
            right_i_stack.append(i)  # 右边小于其高度

        ans = max((right[i] - left[i] - 1) * heights[i] for i in range(n)) if n > 0 else 0
        return ans

从左到右遍历柱子，对于每一个柱子，我们想找到第一个高度小于它的柱子，那么我们就可以使用一个单调递增栈来实现。 如果柱子大于栈顶的柱子，那么说明不是我们要找的柱子，我们把它塞进去继续遍历，如果比栈顶小，那么我们就找到了第一个小于的柱子。 对于栈顶元素，其右边第一个小于它的就是当前遍历到的柱子，左边第一个小于它的就是栈中下一个要被弹出的元素，因此以当前栈顶为最小柱子的面积为当前栈顶的柱子高度 * (当前遍历到的柱子索引 - 1 - (栈中下一个要被弹出的元素索引 + 1) + 1)，化简一下就是 当前栈顶的柱子高度 * (当前遍历到的柱子索引 - 栈中下一个要被弹出的元素索引 - 1)。

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        stack = [-1] # 使用-1来代表开始位置,stack不可能为空，故无需stack判断 
        heights.append(0) # 加入哨兵值，便于原先heights中的最后位置的值弹出,因为需要比最后一个值小的值，才能把最后一个值卡在中间计算面积
        mxarea = 0
        for i, height in enumerate(heights):
            while heights[stack[-1]] > height:
                #当前值比栈顶的值小的时候，相当于两个比栈顶小的值把栈顶位置的数卡在中间，比如3,5，6，2，栈顶数为6
                #此时可以计算栈顶6围成的矩形面积
                mxarea = max(mxarea ,heights[stack.pop()]*(i - stack[-1] - 1 )  )
            stack.append(i) #栈里面后面比前面大的时候才压入，相当于顺序压入
        return mxarea

参考

力扣（LeetCode） (leetcode-cn.com)