离线可持久化数据结构（主席树）

Posted 2021-09-22 iuk11

权值线段树，又称主席树。
权值线段树，每个叶子节点代表一个权值。
每个节点都有权值，表示在当前区间内的数字个数。
以该题为例，数据为1 5 2 6 3 7 4表示要查询的数组a[]。

---

离散化
离散化就是用键值对把所有数据的相隔距离变为1。
例如1008 9 2 2 3数据集，可以通过编号:
map[1]=2;map[2]=3;map[3]=9;map[4]=1008
前提是需要对原数组排序并去重。

//如果我的数据集存在<vector>中
sort(d.begin(),d.end());//排序
d.erase(unique(d.begin(),d.end()),d.end());//去重

如此做我们vector的下标就是键，里面存的就是值。

---

构建权值线段树
root[i] = [1,i]区间的权值线段树的根节点
因为i与i-1要构建树的话只差一个值a[i]，所以我们可以在建好[1,i-1]的前提下，通过二分查找哪些区间(节点)的权值需要加一。因为我们的树是在下标的基础上建立的，所以我们先根据离散化的vector数组d，用low_bound()二分找到a[i]的下标，然后根据下标去搜索在树的哪些区间中，并更新每一个搜索到的节点的权值，直到叶子节点为止。

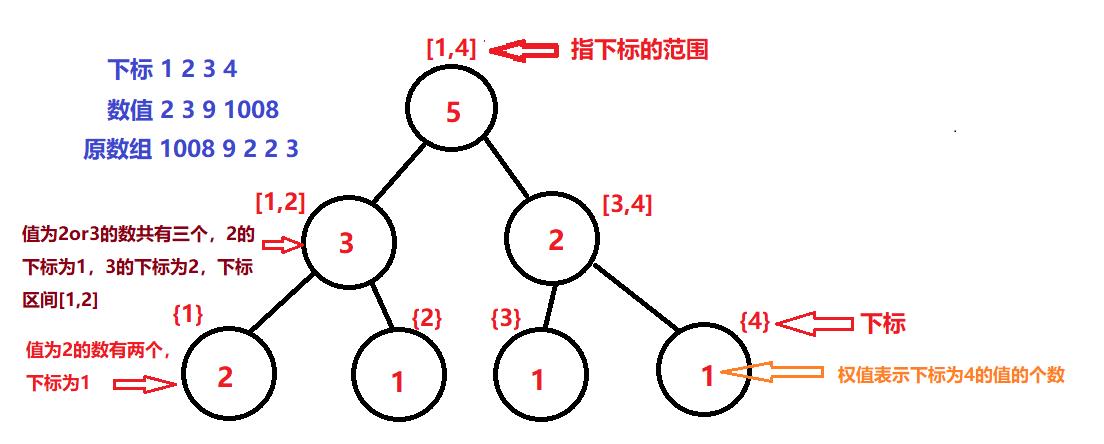
建树的流程如上图，更新点的过程如下图：

补充：因为是点更新，最开始可以不必建树，因为最开始每个点的权值均为0，直接在此基础上更新第一个值即可。

---

代码补充理解
int p=tr[tr[now].l].val-tr[tr[pre].l].val;计算左半边的数字个数
if(k<=p) return query(tr[now].l,tr[pre].l,l,mid,k);如果左半边的个数比k个多，那么第k小的数一定在左边的区间中。
else return query(tr[now].r,tr[pre].r,mid+1,r,k-p);如果左半边的个数比k个少，那么第k小的数就要去右边的区间中找。
直到l=r为止，此时l or r的值即为查询区间内第k小的数的下标。

---

#include<bits/stdc++.h>
using namespace std;
const int N=100010;
int n,m,a[N];
vector<int> d;
int root[N],tot;
struct SegTree{
    int l,r,val;
}tr[N*21];
int find(int x){
    return lower_bound(d.begin(),d.end(),x)-d.begin();
}
int build(int l,int r){
    int p=++tot;
    if(l==r) return p;
    int mid=(l+r)>>1;
    tr[p].l=build(l,mid);
    tr[p].r=build(mid+1,r);
    return p;
}
int update(int pre,int l,int r,int val){
    int p=++tot;
    tr[p]=tr[pre];
    tr[p].val++;
    int mid=(l+r)>>1;
    if(l<r){
        if(val<=mid) tr[p].l=update(tr[pre].l,l,mid,val);
        else tr[p].r=update(tr[pre].r,mid+1,r,val);
    }
    return p;
}
int query(int now,int pre,int l,int r,int k){
    if(l==r) return r;
    int p=tr[tr[now].l].val-tr[tr[pre].l].val;//对位相减
    int mid=(l+r)>>1;
    if(k<=p) return query(tr[now].l,tr[pre].l,l,mid,k);
    else return query(tr[now].r,tr[pre].r,mid+1,r,k-p);
}
int main(){
    ios::sync_with_stdio(false);
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        d.push_back(a[i]);
    }
    sort(d.begin(),d.end());
    d.erase(unique(d.begin(),d.end()),d.end());
    int len=d.size();
    root[0]=build(0,len-1);
    for(int i=1;i<=n;i++){
        root[i]=update(root[i-1],0,len-1,find(a[i]));
    }
    while(m--){
        int l,r,k;
        cin>>l>>r>>k;
        int idx=query(root[r],root[l-1],0,len-1,k);
        cout<<d[idx]<<endl;
    }
    return 0;
}