力扣 221. 最大正方形 [线性DP]

Posted 2021-09-22 布图

题目

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例 1：

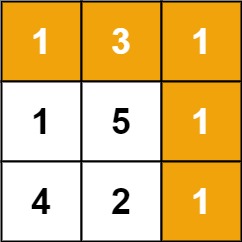
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。
示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 100

解释与代码

暴力写法不说了

我看了一下题解,发现我的想法只差了一点,当然差的是最关键的那一点

状态转移公式,dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1

我看了一下题解上的图片,然后就有灵感了,然后写了下面的代码,过了,虽然是dp,但是比较复杂,可以化简

class Solution {
    public:
    int dp[400][400];
    int maximalSquare(vector<vector<char>>& matrix) {
        int maxx = 0;
        int n = matrix.size(), m = matrix[0].size();
        for (int i=0; i<n; i++) {//dp数组可以用原来的matrix数组来代替
            for (int j=0; j<m; j++) {
                if (matrix[i][j] == '0') {
                    dp[i][j] = 0;
                } else {
                    dp[i][j] = 1;
                }
                maxx = max(maxx, dp[i][j]);
            }
        }
        for (int i=1; i<n; i++) {
            for (int j=1; j<m; j++) {
                if (dp[i-1][j] == dp[i][j-1] && dp[i-1][j] == dp[i-1][j-1]) {//三个相等
                    if (dp[i-1][j] != 0) {//非0
                        if (dp[i][j] == 1 ) {//本节点是1
                            dp[i][j] = dp[i][j-1] + 1;//+1
                        }
                    }
                } else {//三个不等
                    if (dp[i][j] == 1) {//1
                        int minn = min(min(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1]);//找出最小然后+1
                        dp[i][j] = minn + 1;
                    }
                }
                maxx = max(maxx, dp[i][j]);
            }
        }
        return maxx*maxx;
    }
};

化简版:

class Solution {
    public:
    int dp[400][400];
    int maximalSquare(vector<vector<char>>& matrix) {
        int maxx = 0;
        int n = matrix.size(), m = matrix[0].size();
        for (int i=0; i<n; i++) {//dp数组可以用原来的matrix数组来代替
            for (int j=0; j<m; j++) {
                if (matrix[i][j] == '0') {
                    dp[i][j] = 0;
                } else {
                    dp[i][j] = 1;
                }
                maxx = max(maxx, dp[i][j]);
            }
        }
        for (int i=1; i<n; i++) {
            for (int j=1; j<m; j++) {
                if (dp[i][j] == 1) {
                    int minn = min(min(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1]);//找出最小然后+1
                    dp[i][j] = minn + 1;
                }
                maxx = max(maxx, dp[i][j]);
            }
        }
        return maxx*maxx;
    }
};