Leetcode之693.交替位二进制数

Posted 2021-09-22 二木成林

题目

题目描述

给定一个正整数，检查它的二进制表示是否总是 0、1 交替出现：换句话说，就是二进制表示中相邻两位的数字永不相同。

示例 1：

输入：n = 5
输出：true
解释：5 的二进制表示是：101

示例 2：

输入：n = 7
输出：false
解释：7 的二进制表示是：111.

示例 3：

输入：n = 11
输出：false
解释：11 的二进制表示是：1011.

示例 4：

输入：n = 10
输出：true
解释：10 的二进制表示是：1010.

示例 5：

输入：n = 3
输出：false

提示：

• 1 <= n <= 231 - 1

来源

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/binary-number-with-alternating-bits
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题解

解法1

class Solution {
    /**
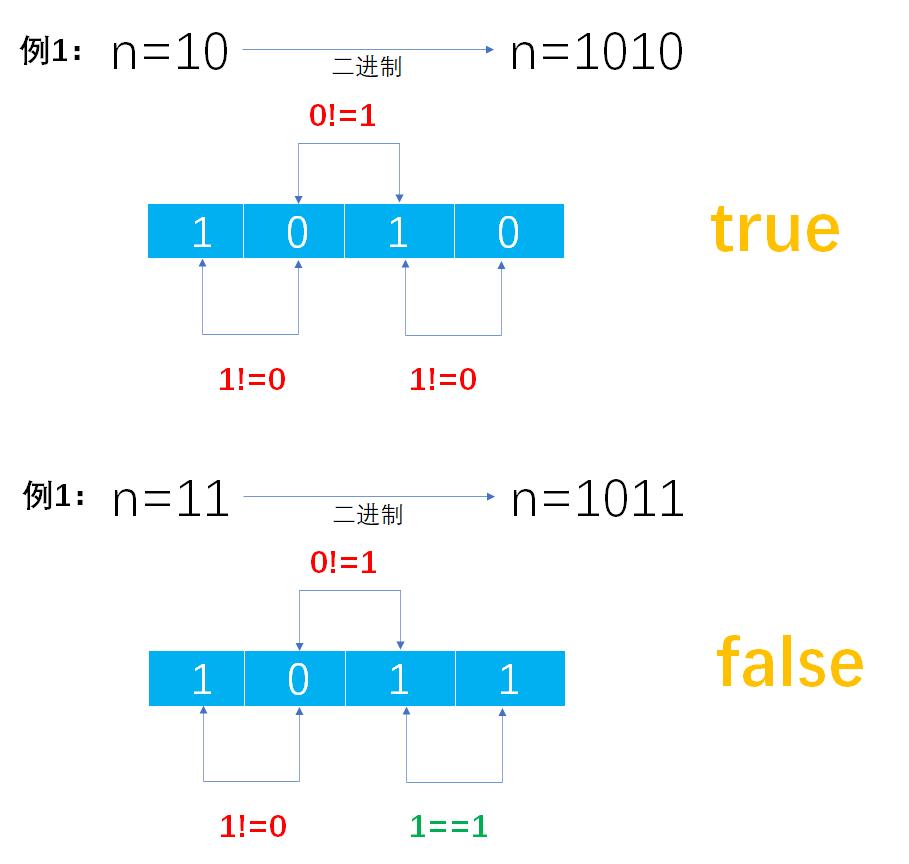
     * <p>思路：将十进制数字转换成二进制字符串，然后判断相邻字符是否相等，如果不等则返回false</p>
     * <p>步骤：</p>
     * <ul>
     *     <li>第一步，将十进制整数转换成二进制字符串，再转换成二进制字符数组</li>
     *     <li>第二步，判断字符数组相邻字符是否不相等，如果存在相等则表示相邻两位数字相同则返回false</li>
     * </ul>
     * <p>结果：成功</p>
     * <ul>
     *     <li>执行用时：1 ms, 在所有 Java 提交中击败了13.21% 的用户</li>
     *     <li>内存消耗：35.1 MB, 在所有 Java 提交中击败了68.23% 的用户</li>
     *     <li>通过测试用例：204 / 204</li>
     * </ul>
     *
     * @param n 十进制数字
     * @return 如果它的二进制数表示总是0、1交替出现则返回true
     */
    public boolean hasAlternatingBits(int n) {
        // 第一步，将十进制整数转换成二进制字符串，再转换成二进制字符数组
        String binaryStr = Integer.toBinaryString(n);
        char[] chars = binaryStr.toCharArray();
        // 第二步，判断字符数组相邻字符是否不相等，如果存在相等则表示相邻两位数字相同则返回false
        for (int i = 0; i < chars.length - 1; i++) {
            if (chars[i] == chars[i + 1]) {
                return false;
            }
        }
        return true;
    }
}

解法2

public class Solution {

    /**
     * <p>思路：使用技巧，只要二进制字符串中不包含"11"和"00"，那么就是交替位二进制数。</p>
     * <p>步骤：</p>
     * <ul>
     *     <li>第一步，将十进制整数转换成二进制字符串。</li>
     *     <li>第二步，直接判断二进制字符串中是否不包含"11"和"00"，只要都不包含则'0'和'1'相邻。</li>
     * </ul>
     * <p>结果：成功</p>
     * <ul>
     *     <li>执行用时：1 ms, 在所有 Java 提交中击败了13.21% 的用户</li>
     *     <li>内存消耗：35 MB, 在所有 Java 提交中击败了88.69% 的用户</li>
     *     <li>通过测试用例：204 / 204</li>
     * </ul>
     *
     * @param n 十进制数字
     * @return 如果它的二进制数表示总是0、1交替出现则返回true
     */
    public boolean hasAlternatingBits(int n) {
        // 第一步，将十进制整数转换成二进制字符串。
        String binaryStr = Integer.toBinaryString(n);
        // 第二步，直接判断二进制字符串中是否不包含"11"和"00"，只要都不包含则'0'和'1'相邻
        return !binaryStr.contains("11") && !binaryStr.contains("00");
    }
}

解法3

public class Solution {

    /**
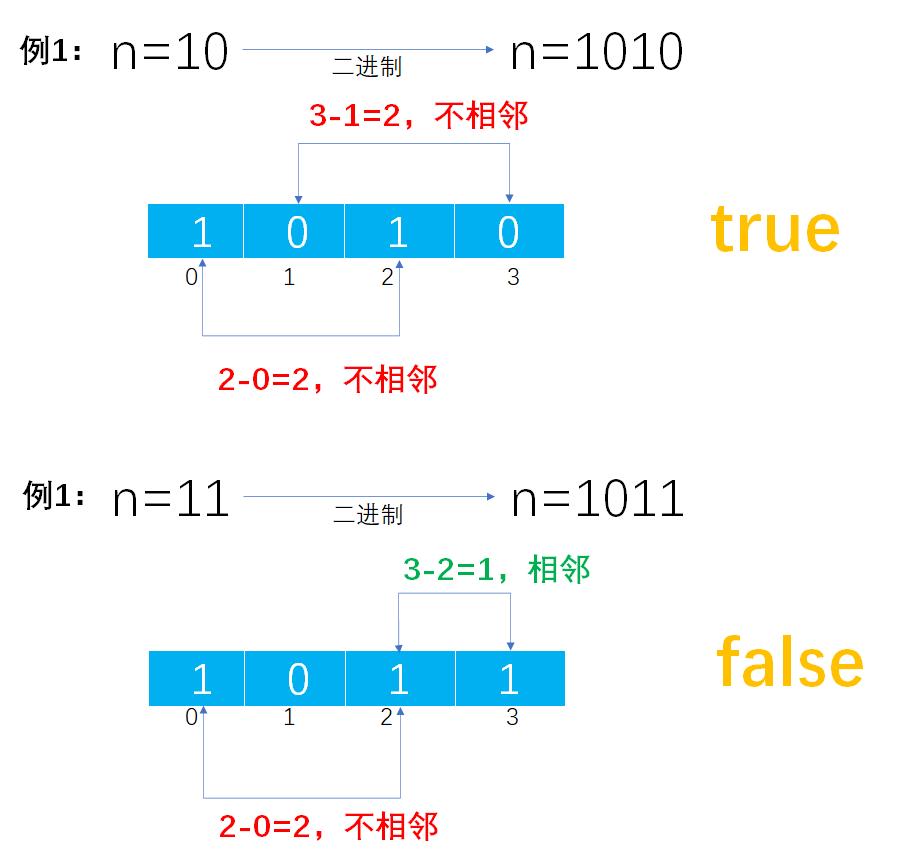
     * <p>思路：用Map集合来存放'0'和'1'字符，Map的键值对中的键存放'0'或'1'字符，而值存放该字符在数组中的索引。如果存在连续的相同字符，它们的索引之差为1；如果存在不连续的相同字符，它们的索引之差为2。</p>
     * <p>步骤：</p>
     * <ul>
     *     <li>第一步，将十进制整数转换成二进制字符串，并且转换成字符数组。</li>
     *     <li>第二步，用一个Map集合来存储'0'和'1'字符，存储每个字符的下标。</li>
     * </ul>
     * <p>结果：成功</p>
     * <ul>
     *     <li>执行用时：1 ms, 在所有 Java 提交中击败了13.21% 的用户</li>
     *     <li>内存消耗：35.2 MB, 在所有 Java 提交中击败了46.76% 的用户</li>
     *     <li>通过测试用例：204 / 204</li>
     * </ul>
     *
     * @param n 十进制数字
     * @return 如果它的二进制数表示总是0、1交替出现则返回true
     */
    public boolean hasAlternatingBits(int n) {
        // 第一步，将十进制整数转换成二进制字符串，并且转换成字符数组
        String binaryStr = Integer.toBinaryString(n);
        char[] chars = binaryStr.toCharArray();
        // 第二步，用一个Map集合来存储'0'和'1'字符，存储每个字符的下标
        Map<Character, Integer> map = new HashMap<>();
        for (int i = 0; i < chars.length; i++) {
            // 如果Map集合中不存在该字符，那么就将该字符存入Map集合中
            if (!map.containsKey(chars[i])) {
                map.put(chars[i], i);
            } else {
                // 如果Map集合中存在该字符，那么表示可以判断两个相同字符是否相邻，如果它们的索引之差为1则表示两个相同字符相邻那么直接返回false，如果索引之差为2则更新该字符的索引
                if (i - map.get(chars[i]) == 2) {
                    map.put(chars[i], i);
                } else {
                    return false;
                }
            }
        }
        return true;
    }
}

解法4

public class Solution {

    /**
     * <p>思路：取余运算，将整数n不断对2取余，获取它的二进制数，来比较相邻是否相等，而last记录上一个二进制位的值。</p>
     * <p>结果：成功</p>
     * <ul>
     *     <li>执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户</li>
     *     <li>内存消耗：35.1 MB, 在所有 Java 提交中击败了77.64% 的用户</li>
     *     <li>通过测试用例：204 / 204</li>
     * </ul>
     *
     * @param n 十进制数字
     * @return 如果它的二进制数表示总是0、1交替出现则返回true
     */
    public boolean hasAlternatingBits(int n) {
        // 记录上一个二进制位的值，初始值为-1，不能为0或1
        int last = -1;
        while (n > 0) {
            // 当前二进制位与上一个二进制位比较，如果相等表示相邻的两位二进制相同，则返回false
            if (last == n % 2) {
                return false;
            }
            // 将当前二进制位赋给last
            last = n % 2;
            // 继续下一次循环
            n /= 2;
        }
        return true;
    }
}

解法5

public class Solution {

    /**
     * <p>思路：运算。交替0和1，移位后异或就可以全为1，再与自身加1后相与一定为0。</p>
     * <p>结果：成功</p>
     * <ul>
     *     <li>执执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户</li>
     *     <li>内存消耗：35.2 MB, 在所有 Java 提交中击败了62.39% 的用户</li>
     *     <li>通过测试用例：204 / 204</li>
     * </ul>
     *
     * @param n 十进制数字
     * @return 如果它的二进制数表示总是0、1交替出现则返回true
     */
    public boolean hasAlternatingBits(int n) {
        /*
            例如：n=4
                第一步，n = (n ^ (n >> 1));
                n=(100 ^ (100 >> 1))=(100 ^ 010)=110
                第二步，(n & (n + 1))==0
                (110 & (110+1))=(110 & 111)=110!=0
           例如：n=5
                第一步，n = (n ^ (n >> 1));
                n=(101 ^ (101 >> 1))=(101 ^ 010)=111
                第二步，(n & (n + 1))==0
                (111 & (111+1))=(0111 & 1000)=0
         */
        n = (n ^ (n >> 1));
        return (n & (n + 1)) == 0;
    }
}