据说跟我学完常见排序算法后会看见一道雨后彩虹❤️
Posted 春风~十一载
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了据说跟我学完常见排序算法后会看见一道雨后彩虹❤️相关的知识,希望对你有一定的参考价值。
排序有很多种,其中的7种比较类排序是面试中经常问到的内容,因此十分重要!下面将由博主用尽可能简单明了易懂的方式带大家去理解它,最终掌握这几个排序方式后,你就会翻越数据结构之排序这座高山,看到那美丽的来之不易的雨后彩虹啦!
先跟着我一起好好学,学到文末后你就会发现惊喜啦!

排序
排序的基本概念
定义
排序是日常生说中包括计算机中经常进行的一项操作,其目的是将一组"无序"的记录序列调整为"有序"的记录序列。
注意:
1.平时上下文中所提到的排序,默认指的是排升序,而非降序
2.所有的排序算法不是只能排数字,任何类型的数据都可以排,只要指定了排序的规则即可,比如可以按进制排
算法稳定性
如果经过排序后,排序算法能保证其相对位置不发生变化,则我们称该算法是具备稳定性的排序算法。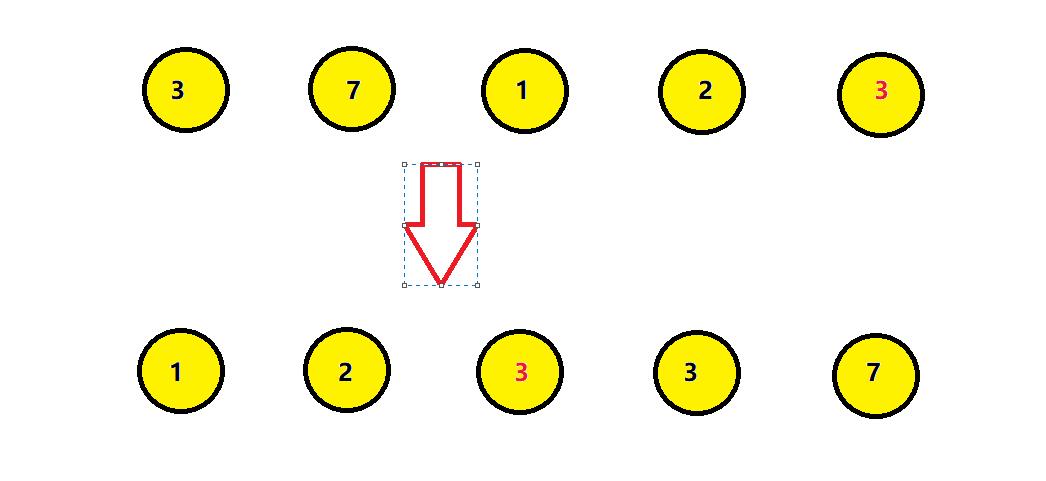
如上图,排好序后红色的3位于黑色的3之前,相对位置发生了改变,则认为这个排序是不稳定的
应用
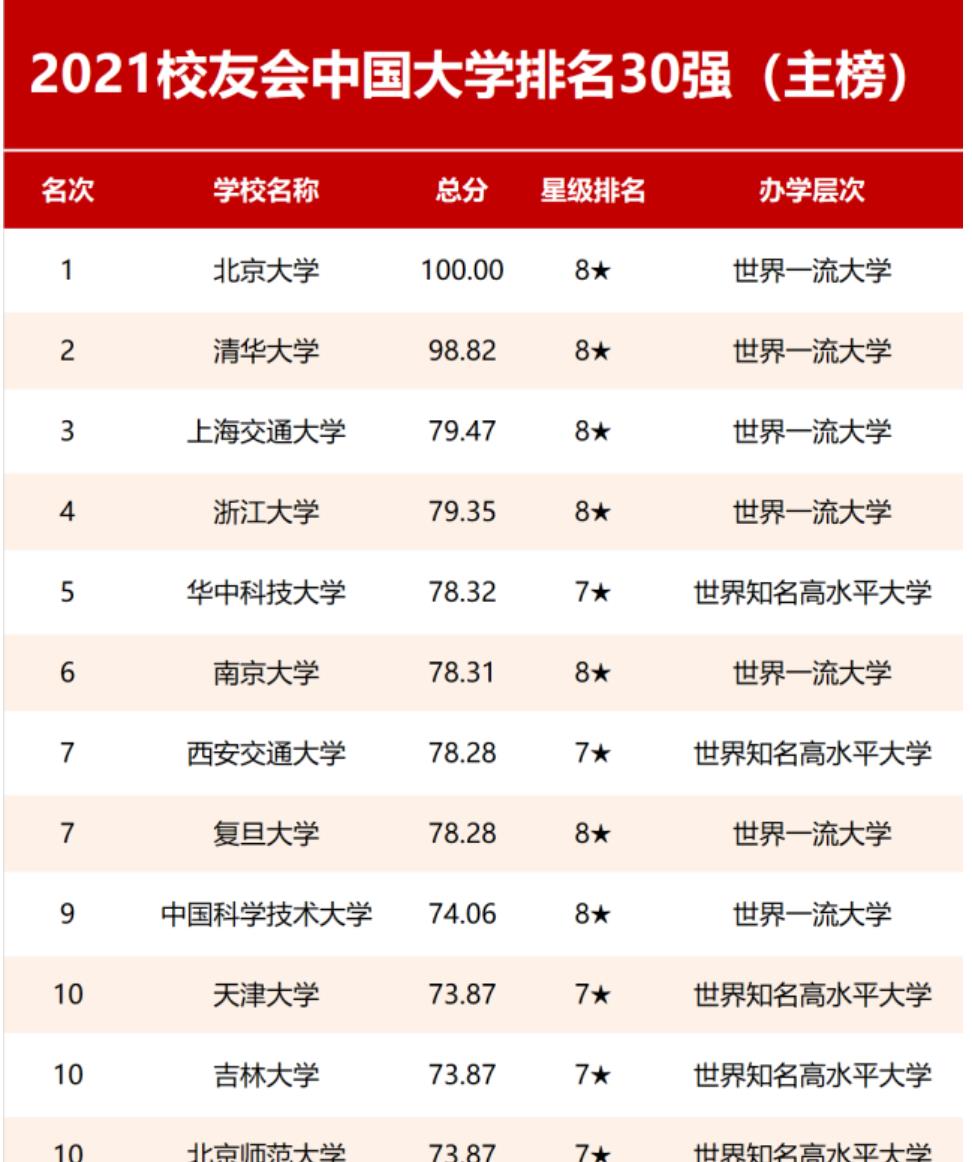
生活中排序的应用有很多,例如大学的排名,成绩的排名等等
插入排序
原理
在一个已经排好的有序数据序列中插入一个数,且要求插入后此数据序列仍然有序,这个时候就要用到一种的排序方法——插入排序法,一般也称直接插入排序。
排序思想
一般来说,插入排序都采用in-place在数组上实现。具体算法描述如下:
-
从第一个元素开始,该元素可以认为已经被排序
-
取出下一个元素,在已经排序的元素序列中从后向前遍历
-
如果该元素(已排序)大于新元素,将该元素移到下一位置
-
重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
-
将新元素插入到该位置后
-
重复步骤2~5
-
如果比较操作的代价比交换操作大的话,可以采用二分查找法来减少比较操作的数目。该算法可以认为是插入排序的一个变种,称为二分查找插入排序。
实现
实现代码:
public static void insertSort(int[] array) {
for(int i = 1;i < array.length;i++) {//n-1
int tmp = array[i];
int j = i-1;
for(; j >= 0;j--) {//n-1
if(array[j] > tmp) {
array[j+1] = array[j];
}else{
//array[j+1] = tmp;
break;
}
}
array[j+1] = tmp;
}
}
排序性能分析
若目标是把n个元素的序列升序排列,那么采用插入排序的最好情况就是,序列已经是升序排列了,在这种情况下,需要进行的比较操作需n-1次即可。最坏情况就是,序列是降序排列,那么此时需要进行的比较共有(1/2)*n(n-1)次。插入排序的赋值操作是比较操作的次数减去n-1次,因为n-1次循环中,每一次循环的比较都比赋值多一个,多在最后那一次比较并不带来赋值)。平均来说插入排序算法复杂度为O(n^2)。因而,插入排序不适合对于数据量比较大的排序应用。但是,如果需要排序的数据量很小,或者若已知输入元素大致上按照顺序排列,那么还是比较适合使用插入排序的
总结
- 时间复杂度:最好:O(N);最坏O(N^2)
- 空间复杂度O(1)
- 稳定性:稳定
- 当一组数据的数据量比较少且趋于有序时,用插入排序比较好
- 数据越有序越快
希尔排序
原理
希尔排序(Shell’s Sort)又称“缩小增量排序”(Diminishing Increment Sort),它也是一种属插入排序类的方法,但在时间 率上较前述几种排序方法有较大的改进。从对直接插入排序的分析得知,其算法时间复杂度为O(n^2),但是,若待排记录序列为“正序”时,其时间复杂度可提高至O(n)。它的基本思想是:先将整个待排记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行一次直接插入排序。
| 简单来说,希尔排序主要的思想是对一组数据进行预排序,当数据逐渐接近有序时再进行整体排序,这样算法的效率会大大提升 |
| 希尔排序的分析是一个复杂的问题,因为它的时间是所取“增量”序列的函数,这涉及一些微学上尚未解决的难题。因此,到目前为止尚未有人求得一种最好的增量序列,增量序列可以有各种取法,但需注意:应使增量序列中的值没有除1之外的公因子,并且最后一个增量值必须等于1。 |
实现

当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果
实现代码:
public static void shell(int[] array,int gap) {
for (int i = gap; i < array.length; i++) {
int tmp = array[i];
int j = i-gap;
for (; j >= 0; j -= gap) {
if(array[j] > tmp) {
array[j+gap] = array[j];
}else {
break;
}
}
array[j+gap] = tmp;
}
}
public static void shellSort(int[] array) {
//处理gap
int gap = array.length;
while (gap > 1) {
gap = gap / 3 + 1;//+1 保证最后一个序列是 1 除几都行
// gap /= 2;
shell(array,gap);
}
}
排序性能分析
由于多次插入排序,我们知道一次插入排序是稳定的,不会改变相同元素的相对顺序,但在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,可理解为元素可能会跳跃式移动,所以最后其稳定性就会被打乱,因此shell排序是不稳定的。
时间复杂度:不同的增量序列会产生不同的时间复杂度,比如有人提出当增量序列为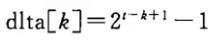
是,其时间复杂度为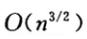
其中t为排序趟数,且: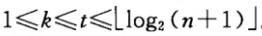
总结:
- 稳定性:不稳定
- 时间复杂度:不确定,但可以记为N(1.3) 到N(1.5) 之间
选择排序
原理
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
实现
实现代码:
public static void selectSort(int[] array) {
for (int i = 0; i < array.length; i++) {
for (int j = i+1; j < array.length; j++) {
if(array[j] < array[i]) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
}
}
}
排序性能分析
选择排序较为简单,其最好的情况和最坏的情况下程序执行的次数是一样的,因此时间复杂度是一个定值
总结
- 时间复杂度:O(N2 )
- 空间复杂度:O(1)
堆排序
原理
- 堆排序是利用堆这种数据结构设计出的一种排序算法,其是选择排序的一种,它利用大顶堆(小顶堆)堆顶元素是最大值(最小值)这一特性,使得每次从无序中选择最大值(最小值)变得简单。
- 排升序要建大堆;排降序要建小堆。
具体步骤如下
step1:先将带排序的数组构造成一个大根堆,假设有如下数组:int[] array2={2,3,4,1,6,5};
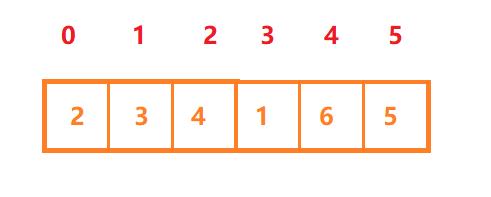
构造成大根堆如下:
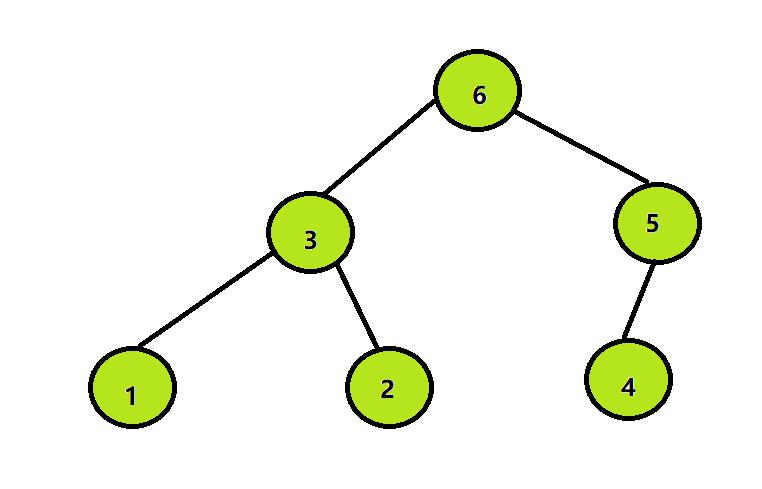
step2:将堆顶元素与堆尾元素交换: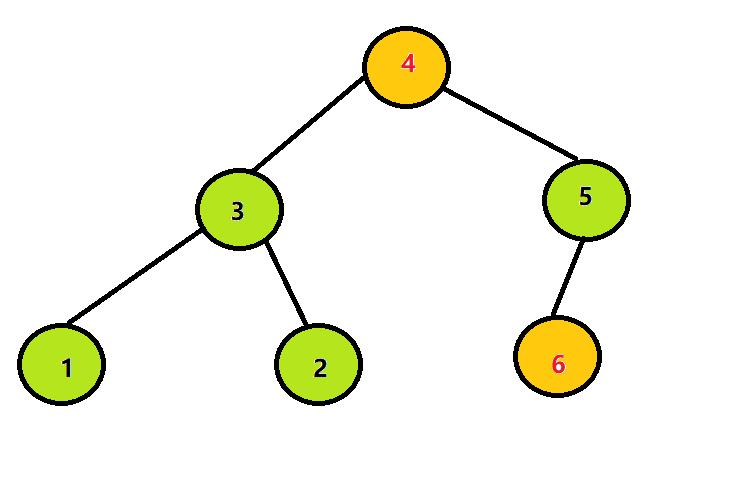
step3:将除6以外其他的所有元素继续构造大根堆: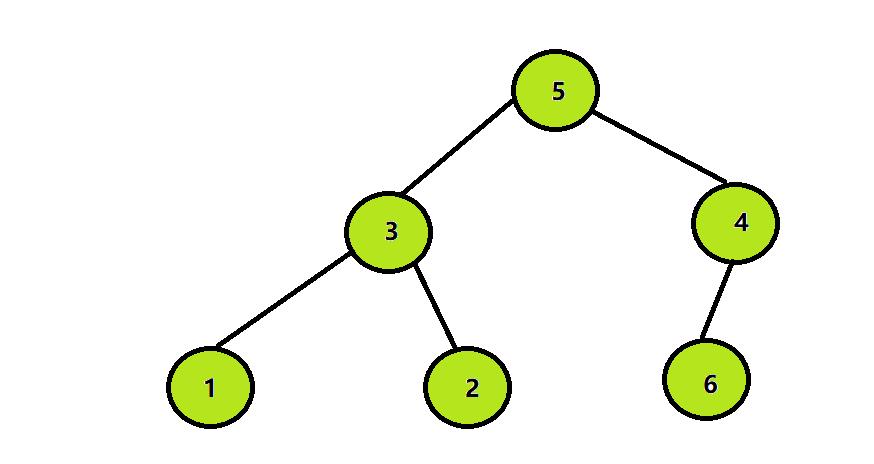
以此类推,然后再将堆顶元素与堆中倒数第二个元素交换,换完之后除了倒数第一个和倒数第二个元素以外,其他元素继续构造成大堆,最终会得到有序的数组
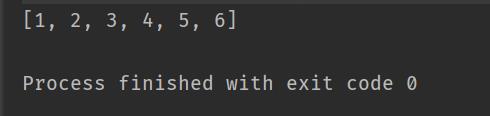
同理,如果要从大到小排,则构建小堆即可!
实现
public static void siftDown(int[] array,int root,int len) {
int parent = root;
int child = 2*parent+1;
while (child < len) {
//找到左右孩子的最大值
//1、前提是你得有右孩子
if(child+1 < len && array[child] < array[child+1]) {
child++;
}
//child的下标就是左右孩子的最大值下标
if(array[child] > array[parent]) {
int tmp = array[child];
array[child] = array[parent];
array[parent] = tmp;
parent = child;
child = 2*parent+1;
}else {
break;
}
}
}
public static void createHeap(int[] array) {
//从小到大排序 -》 大根堆
for (int i = (array.length-1 - 1) / 2; i >= 0 ; i--) {
siftDown(array,i,array.length);
}
}
public static void heapSort(int[] array) {
createHeap(array);//O(n)
int end = array.length-1;
while (end > 0) {//O(N*logN)
int tmp = array[end];
array[end] = array[0];
array[0] = tmp;
siftDown(array,0,end);
end--;
}
}
排序性能分析
- 时间复杂度:O(N* log(N))(最好和最坏的都是这个)
- 空间复杂度:O(1)(在整个调整的过程中并没有重新定义数组)
- 稳定性:不稳定
这个堆排序我上一篇博客中有详细地讲过哦,相信大家看完后一定会有收获的有关堆的相关知识点

冒泡排序
原理
冒泡排序(Bubble Sort)是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。一直重复进行上述步骤,直到没有元素再需要交换,也就是说该数列已经排序完成。
实现
public static void bubbleSort(int[] array) {
for (int i = 0; i < array.length-1; i++) {
for (int j = 0; j < array.length-1-i; j++) {
if(array[j] > array[j+1]) {
int tmp = array[j];
array[j] = array[j+1];
array[j+1] = tmp;
flg = true;
}
}
}
}
排序性能分析
- 时间复杂度:最好/最坏:O(N2 ),若优化,则最好的情况下时间复杂度为O(n)
- 空间复杂度:O(1)
- 稳定性:稳定
优化方法
public static void bubbleSort(int[] array) {
// boolean flg = false;
for (int i = 0; i < array.length-1; i++) {
boolean flg = false;
for (int j = 0; j < array.length-1-i; j++) {
if(array[j] > array[j+1]) {
int tmp = array[j];
array[j] = array[j+1];
array[j+1] = tmp;
flg = true;
}
}
if(flg == false) {
break;
}
}
}
设置一个flg,若当前排序时已经有序,可以提前结束本次循环
快速排序
原理
- 快速排序是对冒泡排序的一种改进。
- 排序前首先选择一个基准值(pivot)将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再对左右两个区间选取基准值,重复此步骤,采用分治思想,对左右两个小区间按照同样的方式处理,直到小区间的长度为1,代表已经有序,或者小区间的长度为0,代表没有数据,排序完成!整个排序过程可以递归进行,也可以非递归进行(如使用栈)
基准的选取(递归实现快速排序)
挖坑法
定义两个变量,假如数组的首元素位置下标是low,数组的尾元素位置下标是high,挖坑法为固定位置选取基准法,比如让low下标的元素作为基准,让其存到临时变量tmp当中,然后将high从后往前遍历,找比tmp的值小的数字,若找到,则将这个值存到low下标对应的位置中。接着让low从左到右遍历去找比tmp的值大的元素,若找到,则将其值存到high下标对应的位置中,以此循环。直到low和high相遇,那么就把tmp的值放到相遇位置作为基准即可。这样即可实现把要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小了
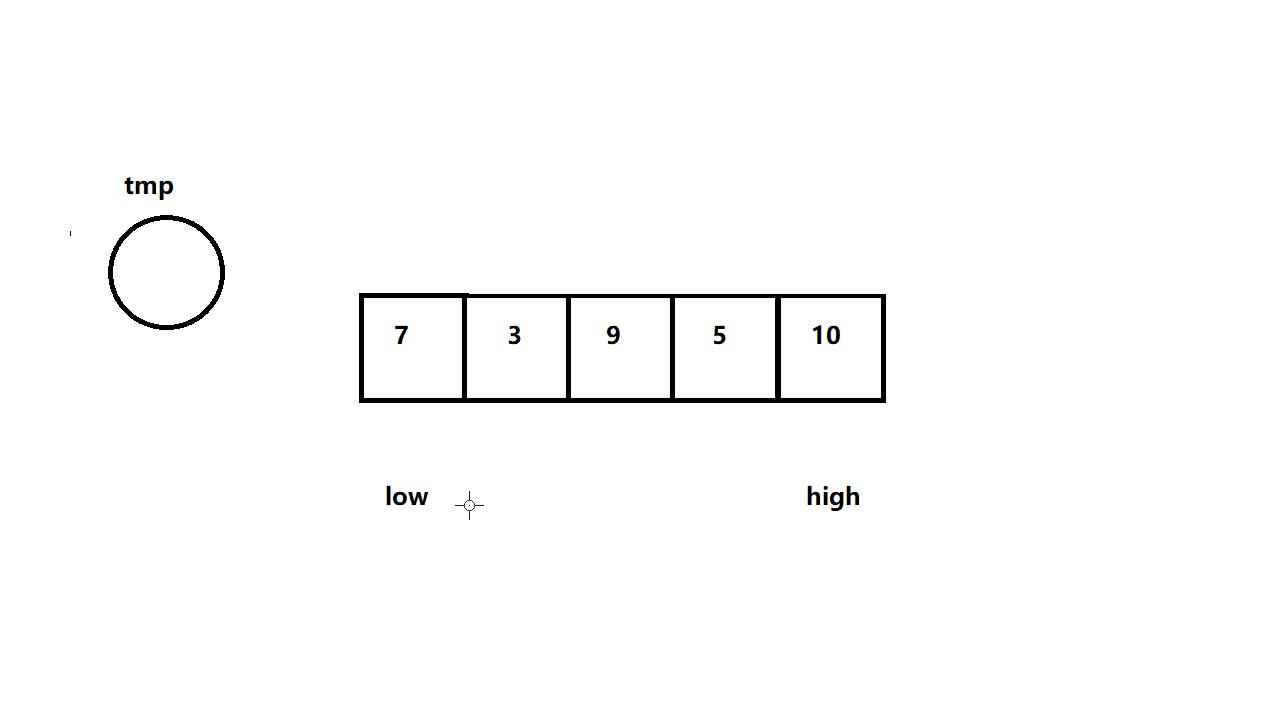
实现代码:
public static int partition(int[] array,int low,int high) {
int tmp = array[low];
while (low < high) {
while (low < high && array[high] >= tmp) {
high--;
}
array[low] = array[high];
while (low < high && array[low] <= tmp) {
low++;
}
array[high] = array[low];
}
array[low] = tmp;
return low;
}
有了基准后,就可以进行快速排序的下一步了,然后再对左右两个小区间选取基准值进行排序,下面我们将使用递归的方法:
import java.util.Arrays;
public class TestDemo {
public static int partition(int[] array,int low,int high) {
int tmp = array[low];
while (low < high) {
while (low < high && array[high] >= tmp) {
high--;
}
array[low] = array[high];
while (low < high && array[low] <= tmp) {
low++;
}
array[high] = array[low];
}
array[low] = tmp;
return low;
}
public static void quick(int[] array,int start,int end) {
if(start >= end) {
return;
}
int pivot = partition(array,start,end);
quick(array,start,pivot-1);
quick(array,pivot+1,end);
}
public static void quickSort1(int[] array) {
quick(array,0,array.length-1);
}
public static void main(String[] args) {
int[] array={12,5,37,41,55,28,6,1,69,17};
quickSort1(array);
System.out.println(Arrays.toString(array));
}
}
打印的结果为: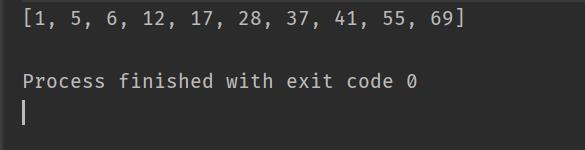
排序完成!
性能分析
- 时间复杂度:
最好情况:O(N*logN)(每一次排序时分割区间都是均匀的)
最坏情况:O(N2)(对已经有序的一对数据排序)
- 空间复杂度:
最好:O(logN)
最坏:O(N)
- 稳定性:不稳定
三数取中
对于上述用挖坑法递归进行快速排序时,因为空间复杂度为O(n),那么当数据足够多时且越趋于有序而导致排序分割的区间不均匀时,那可能会栈溢出(因为递归是在栈上开辟内存的),因此,我们可以用三数取中来实现让排序的区间更趋于均匀,从而提升算法的效率。
具体思路:
让low下标等于数组首元素位置,让high等于数组最后一个元素的位置,定义一个mid使其等于数组的中间位置,然后让low下标的值等于这三个下标对应的值第二大的,即中间大小的值
实现代码:
mport java.util.Arrays;
public class TestDemo {
public static int partition(int[] array,int low,int high) {
int tmp = array[low];
while (low < high) {
while (low < high && array[high] >= tmp) {
high--;
}
array[low] = array[high];
while (low < high && array[low] <= tmp) {
low++;
}
array[high] = array[low];
}
array[low] = tmp;
return low;
}
public static void swap(int[] array,int i,int j) {
int tmp = array[i];
array[i