路径规划 | 图解A*DijkstraGBFS算法的异同(附C++/Python/Matlab仿真)
Posted Mr.Winter`
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了路径规划 | 图解A*DijkstraGBFS算法的异同(附C++/Python/Matlab仿真)相关的知识,希望对你有一定的参考价值。
目录
0 专栏介绍
🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索、采样法、智能算法等);局部规划(DWA、APF等);曲线优化(贝塞尔曲线、B样条曲线等)。
🚀详情:图解自动驾驶中的运动规划(Motion Planning),附几十种规划算法
1 栅格地图与邻域
搜索(Search)是指从初始状态(节点)出发寻找一组能达到目标的行动序列(或称问题的解)的过程。
在图搜索中,往往将环境简化为栅格地图(Grid Map),易于刻画固定场景,同时也便于计算机控制系统进行信息处理。所谓栅格就是将连续地图用固定大小正方形方格进行离散化的单位。
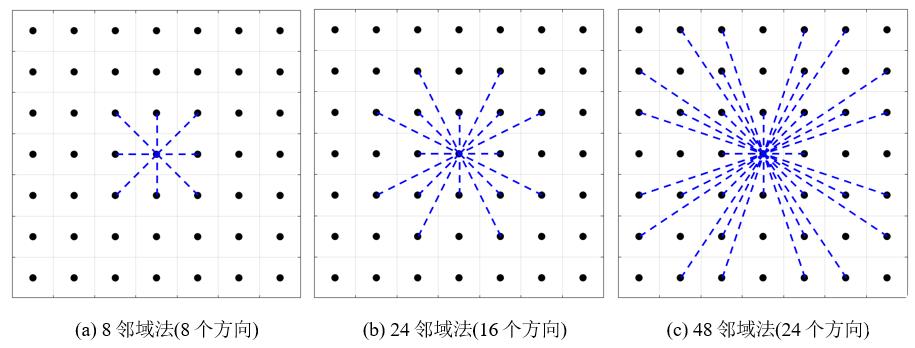
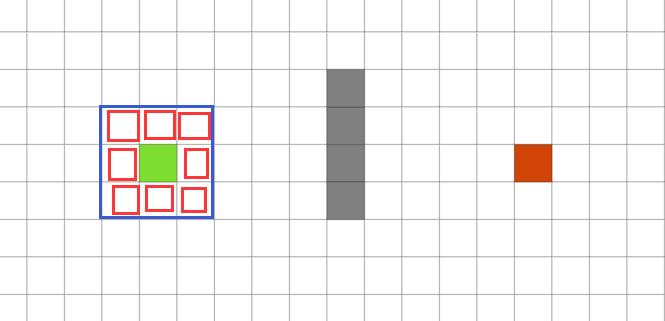
在栅格地图中,常见的邻域(neighbor)模式如下所示,即
- 8邻域
- 24邻域
- 48邻域
栅格的邻域表示了从当前位置出发下一次搜索的集合,例如八邻域法中,当前栅格只能和周围的八个栅格相连形成局部路径。
下面是一个图搜索问题的例子,可以直观理解什么是搜索问题。
例1:在如下的栅格地图中,设绿色栅格为起点,红色栅格为终点,灰色栅格为障碍,白色栅格为可行点,问如何设计一条由栅格组成的连接起点、终点的路径,并尽可能使路径最短?
接下来,围绕这个问题展开阐述。
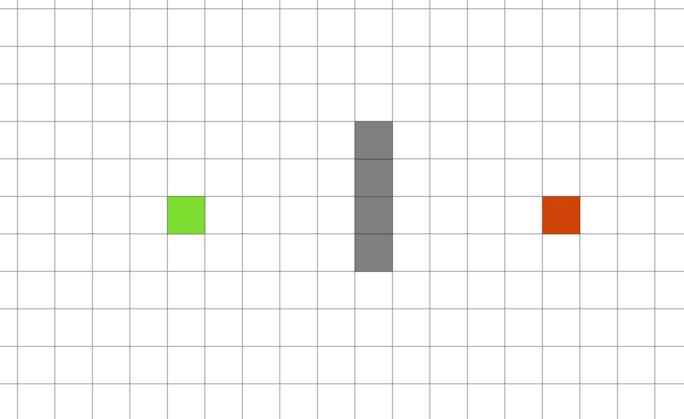
2 贪婪最佳优先搜索
一个朴素的想法是:每一次搜索时就找那些与终点最近的节点,这里衡量最近可以用多种度量方式——曼哈顿距离、欧式距离等。这种方法像一头狼贪婪地望着食物,迫切寻求最近的路径,因此称为贪婪最佳优先搜索(Greedy Best First Search, GBFS)。
假设采用八邻域法,在GBFS思想指导下,在起点的八邻域中就会选择最右侧的节点,如下所示。
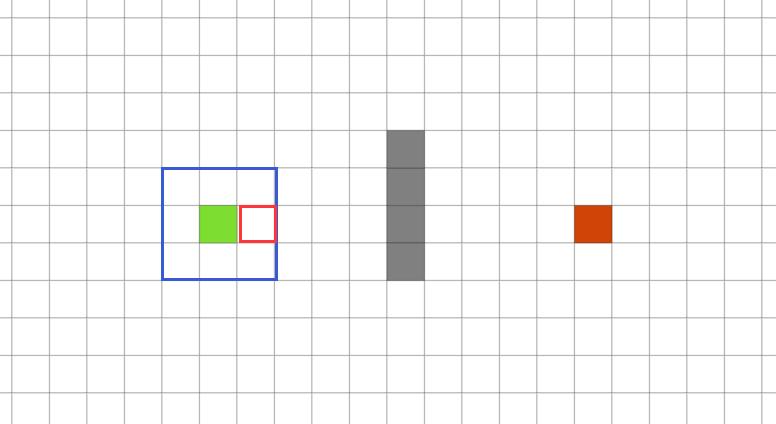
循环地,直到如下所示的节点,因为邻域内有障碍,这些障碍节点不会被候选,所以此时离终点最近的就是下方的方格
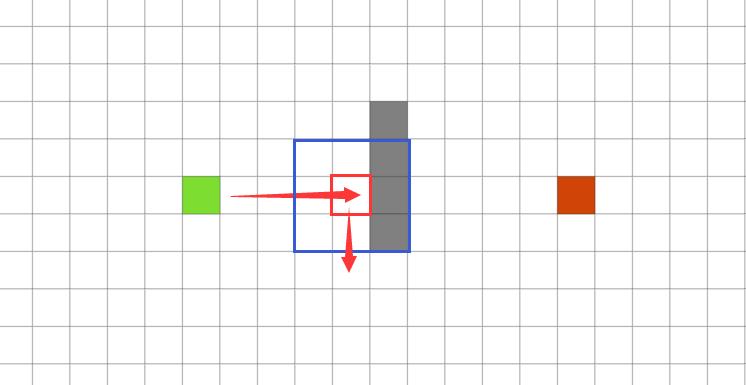
依次类推直至终点
3 Dijkstra算法
Dijkstra算法走向了另一个极端,它完全不考虑扩展节点与终点的关系,而是定义了一个路径耗散函数 g ( n ) g(n) g(n),从起点开始,机器人每走一个栅格就会产生一定的代价或耗散,因为Dijkstra算法希望路径最短,所以每次首选那些使路径耗散最小的节点。
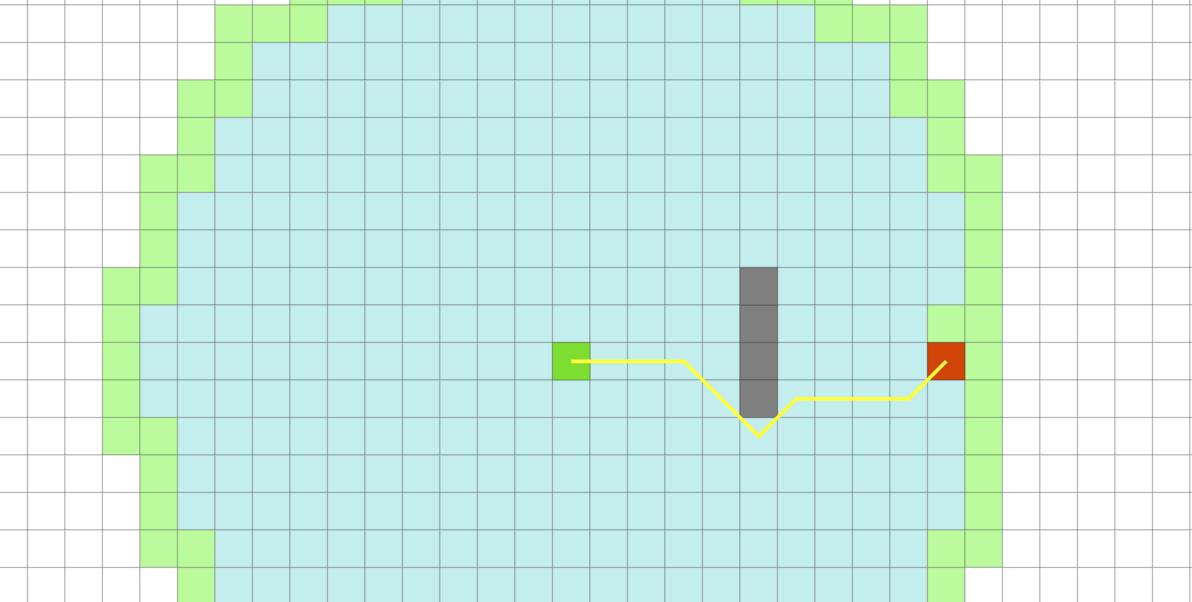
依照Dijkstra算法的观点,从起点开始,其八个邻域节点都会被依次探索,因为它们离起点最近,接着再探索这些节点的子节点。
因此Dijkstra算法会遍历大量的节点,一圈圈地逼近终点
4 启发式A*搜索
A*算法是非常有效且常用的路径规划算法之一,其是结合Dijsktra算法与GBFS各自优势的启发式搜索算法,其搜索代价评估函数为
f ( n ) = g ( n ) + h ( n ) f(n)=g(n)+h(n) f(n)=g(n)+h(n)
其中 g ( n ) g(n) g(n)代表路径耗散,是Dijsktra算法分量; h ( n ) h(n) h(n)代表下一个搜索节点与终点的距离,启发式地引导机器人朝着终点拓展,是GBFS算法分量。

兼具两个算法特点的A*算法既保持完备性,又在一定条件下体现出最优性,被广泛应用于路径规划中。
5 A*、Dijkstra、GBFS算法的异同
特别地
- 当 g ( n ) = 0 g\\left( n \\right) =0 g(n)=0时,启发函数影响占据主导,A*算法退化为GBFS算法——完全不考虑状态空间本身的固有属性,不择手段地追求对目标的趋近,此时算法搜索效率将得到提升,但最优性无法保证;
- 当 h ( n ) = 0 h(n)=0 h(n)=0时,路径耗散函数影响占据主导,A*算法退化为Dijsktra算法——无先验信息搜索,此时算法搜索效率下降,但最优性上升。
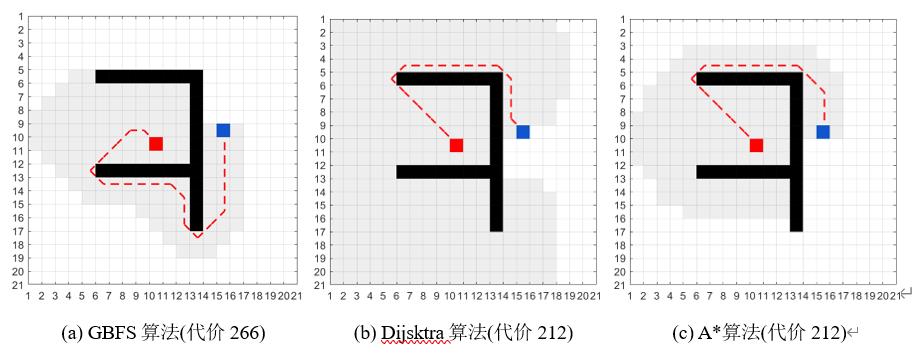
三个算法的直观比较如下所示
6 算法仿真与实现
6.1 算法流程

6.2 ROS C++实现
核心代码如下
std::tuple<bool, std::vector<Node>> AStar::plan(const unsigned char* costs, const Node& start,
const Node& goal, std::vector<Node> &expand)
// open list
std::priority_queue<Node, std::vector<Node>, compare_cost> open_list;
open_list.push(start);
// closed list
std::unordered_set<Node, NodeIdAsHash, compare_coordinates> closed_list;
// expand list
expand.clear();
expand.push_back(start);
// get all possible motions
const std::vector<Node> motion = getMotion();
// main loop
while (!open_list.empty())
// pop current node from open list
Node current = open_list.top();
open_list.pop();
current.id = this->grid2Index(current.x, current.y);
// current node do not exist in closed list
if (closed_list.find(current) != closed_list.end())
continue;
// goal found
if (current==goal)
closed_list.insert(current);
return true, this->_convertClosedListToPath(closed_list, start, goal);
// explore neighbor of current node
for (const auto& m : motion)
Node new_point = current + m;
// current node do not exist in closed list
if (closed_list.find(new_point) != closed_list.end())
continue;
// explore a new node
new_point.id = this->grid2Index(new_point.x, new_point.y);
new_point.pid = current.id;
// if using dijkstra implementation, do not consider heuristics cost
if(!this->is_dijkstra_)
new_point.h_cost = std::sqrt(std::pow(new_point.x - goal.x, 2)
+ std::pow(new_point.y - goal.y, 2));
// if using GBFS implementation, only consider heuristics cost
if(this->is_gbfs_)
new_point.cost = 0;
// goal found
if (new_point==goal)
open_list.push(new_point);
break;
// bext node hit the boundary or obstacle
if (new_point.id < 0 || new_point.id >= this->ns_ ||
costs[new_point.id] >= this->lethal_cost_ * this->factor_)
continue;
open_list.push(new_point);
expand.push_back(new_point);
closed_list.insert(current);
return false, ;
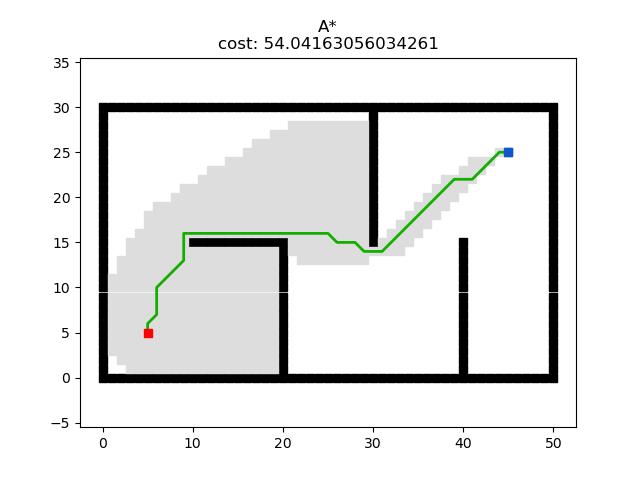
6.3 Python实现
核心代码如下
def plan(self):
# OPEN set with priority and CLOSED set
OPEN = []
heapq.heappush(OPEN, self.start)
CLOSED = []
while OPEN:
node = heapq.heappop(OPEN)
# exists in CLOSED set
if node in CLOSED:
continue
# goal found
if node == self.goal:
CLOSED.append(node)
return self.extractPath(CLOSED), CLOSED
for node_n in self.getNeighbor(node):
# exists in CLOSED set
if node_n in CLOSED:
continue
node_n.parent = node.current
node_n.h = self.h(node_n, self.goal)
# goal found
if node_n == self.goal:
heapq.heappush(OPEN, node_n)
break
# update OPEN set
heapq.heappush(OPEN, node_n)
CLOSED.append(node)
return [], []
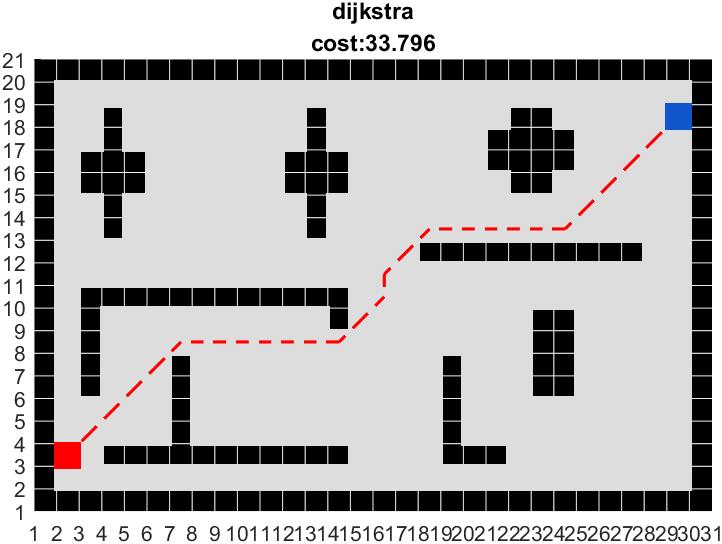
6.4 Matlab实现
核心代码如下
while ~isempty(OPEN(:, 1))
% pop
f = OPEN(:, 3) + OPEN(:, 4);
[~, index] = min(f);
cur_node = OPEN(index, :);
OPEN(index, :) = [];
% exists in CLOSED set
if loc_list(cur_node, CLOSED, [1, 2])
continue
end
% goal found
if cur_node(1) == goal(1) && cur_node(2) == goal(2)
CLOSED = [cur_node; CLOSED];
flag = true;
cost = cur_node(3);
break
end
% explore neighbors
for i=1:neighbor_num
node_n = [cur_node(1) + neighbor(i, 1), ...
cur_node(2) + neighbor(i, 2), ...
cur_node(3) + neighbor(i, 3), ...
0, cur_node(1), cur_node(2)
];
node_n(4) = h(node_n(1:2), goal);
% exists in CLOSED set
if loc_list(cur_node, CLOSED, [1, 2])
continue
end
% obstacle
if map(node_n(1), node_n(2)) == 2
continue;
end
% goal found
if cur_node(1) == goal(1) && cur_node(2) == goal(2)
CLOSED = [cur_node; CLOSED];
flag = true;
cost = cur_node(3);
break
end
% update expand zone
expand = [expand; node_n(1:2)];
% update OPEN set
OPEN = [OPEN; node_n];
end
CLOSED = [cur_node; CLOSED];
end
🔥 更多精彩专栏:
以上是关于路径规划 | 图解A*DijkstraGBFS算法的异同(附C++/Python/Matlab仿真)的主要内容,如果未能解决你的问题,请参考以下文章