Pandas高级数据分析快速入门之五——机器学习特征工程篇

Posted 2021-09-21 肖永威

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Pandas高级数据分析快速入门之五——机器学习特征工程篇相关的知识，希望对你有一定的参考价值。

Pandas高级数据分析快速入门之一——Python开发环境篇
Pandas高级数据分析快速入门之二——基础篇
Pandas高级数据分析快速入门之三——数据挖掘与统计分析篇
Pandas高级数据分析快速入门之四——数据可视化篇
Pandas高级数据分析快速入门之五——机器学习特征工程篇
Pandas高级数据分析快速入门之六——机器学习预测分析篇

0. Pandas高级数据分析使用机器学习概述

需求	解决方案	技术方案
时序趋势	斜率	线性回归算斜率，Scipy.stats.linregress
正常状态	聚类数据密度，最多的均值	聚类数据密度，SKlearn DBScan
数据相关性	相关性分析	相关系数，Pearson相关系数
预测两种状态	聚类分析	聚类，SKlearn KMean
数据可比性	归一化、标准化	数据标准化，sklearn StandardScaler

1. 线性回归计算斜率和方差

在Python科学计算包Scipy的统计模块stats 中，有 linregress 函数可以做一元线性回归，返回斜率、截距、相关系数、p值和标准误差。

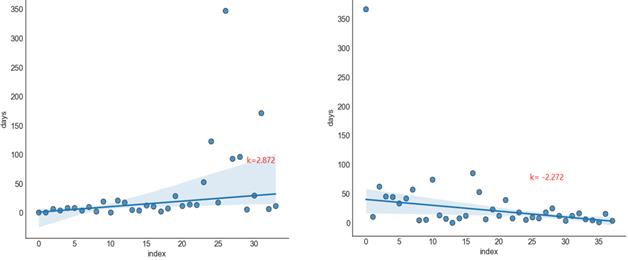
交易间隔天数趋势回归斜率，左侧为典型流失情况， $K_{∆t}=2.872$ ；右侧为不流失正常情况， $K_{∆t}=-2.272$ 。

计算斜率和方差

scipy.stats.linregress(x, y=None)

参数：

输入数据x，y，类数组
两组测量值。两个数组的长度应该相同。如果只给出了x（y=None），那么它必须是一个二维数组，其中一个维度的长度为2。然后通过沿长度为2的维度拆分数组来找到两组测量值。

返回值：

斜率、截距、相关系数、p值和标准误差。

本文涉及到的交易数据，参照上篇博文[1]描述获取数据集及其DataFrame，此处略。

from scipy import stats

def stats_linear_regression(df):
    user_df = df.loc[df['carduser_id']== 2085603 ].reset_index(drop=True)
       
    Days = user_df['days'].values
    Days = Days[1:]
    k = []
    for i in range(len(Days)):
        k.append(i)
    #Days = Days.reshape(-1,1)
    x = np.array(k)
    y = Days
    # 科学计算包中统计方法，用于计算散点回归线趋势的斜率、截距
    slope, intercept, r_value, p_value, std_err = stats.linregress(x, y) 
    print('slope is ' + str(slope))
    
    # 画图
    plt.rcParams['figure.figsize']= 10,5 #设置图例尺寸
    plt.rcParams['font.sans-serif']=['SimHei'] #设置为中文黑体，如果设置楷体则为 KaiTi
    plt.rcParams['axes.unicode_minus']=False

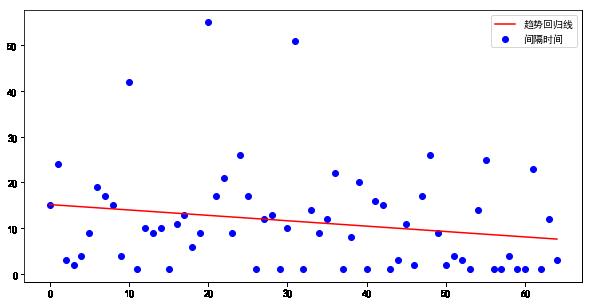
    plt.scatter(x, y, color='b',label='间隔时间')
    plt.plot(x, slope*x + intercept, color='r',label='趋势回归线')
    plt.legend()      #绘制图例，右上角标识图
    plt.show()

stats_linear_regression(trade_df)

slope is -0.11791958041958041

2. 数据密度计算正常状态/周期

基于聚类——数据密度（DBSCAN）提取典型（正常状态）特征，DBSCAN是基于一组邻域来描述样本集密度的空间聚类算法，将具有足够密度的区域划分为簇，参数 $(ϵ, M i n P t s)$ 用来描述邻域的样本分布紧密程度。其中， $ϵ$ 描述了某一样本的邻域距离阈值， $M i n P t s$ 描述了某一样本的距离为ϵ的邻域中样本个数的阈值。

通过DBSCan聚类分析各个客户交易行为规律，设 $∆ t$ 为 $x$ ，使用交易间隔天数的密度分簇，寻找最大的簇为“平常交易间隔天数 $μ_t$ ”，与交易间隔天数平均值、中位数、众数相比，更接近实际情况。
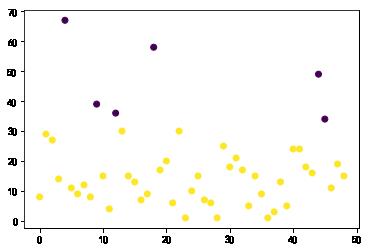
例如图所示交易序列，中位数为15，均值为19.5，聚类最大簇的平均间隔时间μ_t为12天。

sklearn.cluster.DBSCAN参数

sklearn.cluster.DBSCAN(eps=0.5, *, min_samples=5, metric=‘euclidean’, metric_params=None, algorithm=‘auto’, leaf_size=30, p=None, n_jobs=None)

参数：

eps：两个样本之间的最大距离，其中一个样本被视为在另一个样本的邻域中。这不是簇内点距离的最大界限。这是为数据集和距离函数选择的最重要的DBSCAN参数。
min_samples：最小采样点，默认值=5
将一个点视为核心点的邻域中的样本数（或总权重）。
metric：或可调用，默认值为“欧几里德”。
计算要素阵列中实例之间的距离时使用的度量。如果metric是字符串或可调用，则它必须是sklearn.metrics.pairwise_distance为其metric参数所允许的选项之一。若度量是“预计算”的，则假定X是距离矩阵，且必须是平方。X可以是术语表，在这种情况下，只有“非零”元素可以被视为DBSCAN的邻居。
leaf_size，默认值=30。
传递给BallTree或cKDTree的叶大小。这可能会影响构造和查询的速度，以及存储树所需的内存。最佳值取决于问题的性质。
n_jobs，整形数。　指定计算所用的进程数。内部原理是同时进行n_init指定次数的计算。
（１）若值为 -1，则用所有的CPU进行运算。若值为1，则不进行并行运算，这样的话方便调试。
（２）若值小于-1，则用到的CPU数为(n_cpus + 1 + n_jobs)。因此如果 n_jobs值为-2，则用到的CPU数为总CPU数减1。

属性：

labels_：给fit()的数据集中每个点的cluster label。噪声样本的标签为-1。

from sklearn.cluster import DBSCAN
from numpy import unique
import matplotlib.pyplot as plt

# 数据密度分析
def dbcsan_analysis(df): 
    user_df = df.loc[df['carduser_id']== 2085728 ].reset_index(drop=True)
       
    Days = user_df['days'].values
    Days = Days[1:]
    k = []
    for i in range(len(Days)):
        k.append(i)

    Days = Days.reshape(-1,1)
    dbs = DBSCAN(eps = 3, min_samples = 5).fit(Days)
    labels = dbs.labels_ 

    # 检索唯一群集
    clusters = unique(labels)
    k = np.array(k)
    k = k.reshape(-1)
    Days = Days.reshape(-1)
    
    plt.rcParams['font.sans-serif']=['SimHei'] #显示中文标签 KaiTi
    plt.rcParams['axes.unicode_minus']=False

    scatter = plt.scatter(k, Days, c=labels ,cmap='viridis') #'inferno')
    plt.show()  
    
    sub_df = user_df.drop(index=[0]).reset_index(drop=True) # 删除第一行，因为第一行的时间间隔不合理，或者不存在
    Days = sub_df[['days']].copy() # 间隔时间，建立副本处理
    Days['lables'] = labels
    Days = Days.loc[Days['lables']!=-1].reset_index(drop=True)

    count_group = Days[['lables','days']].groupby(by=['lables'],as_index=False).count()
    maxcount= count_group.sort_values(by=['days'], ascending = True).tail(1)[['lables']].values[0][0]
    
    count_mean = Days[['lables','days']].groupby(by=['lables'],as_index=False).mean()
    count_mean['days']= count_mean['days'].round(0)
    DBSan_mean = count_mean[['days']].loc[count_mean['lables']==maxcount].values[0][0]
    mean = Days[['days']].mean()
    
    median = Days[['days']].median()
    
    print(DBSan_mean)
    print(mean)
    print(median)
    
dbcsan_analysis(trade_df)

14.0
days    17.673469
days    15.0

3. 相关分析计算特征间关系

皮尔森相关系数 (Pearson Correlation) 是一种最简单的，能帮助理解特征和响应变量之间关系的方法，该方法衡量的是变量之间的线性相关性，结果的取值区间为 $[- 1 ， 1]$ ，-1表示完全的负相关，+1表示完全的正相关，0表示没有线性相关。

$\\rho_{X,Y}=\\frac{cov(X,Y)}{\\sigma _{X}\\sigma_{Y}}$

$\\rho_{X,Y}=\\frac{\\sum_{i=1}^{n}(X_{i}-\\overline{X})(Y_{i}-\\overline{Y})}{\\sqrt{\\sum_{i=1}^{n}(X-\\overline{X})^{2}}\\sqrt{\\sum_{i=1}^{n}(Y-\\overline{Y})^{2}}}$

DataFrame.corr(method=‘pearson’, min_periods=1)

参数说明：

method：可选值为{‘pearson’, ‘kendall’, ‘spearman’}

pearson：Pearson相关系数来衡量两个数据集合是否在一条线上面，即针对线性数据的相关系数计算，针对非线性数据便会有误差。
kendall：用于反映分类变量相关性的指标，即针对无序序列的相关系数，非正太分布的数据
spearman：非线性的，非正太分布的数据的相关系数

min_periods：样本最少的数据量

返回值：各类型之间的相关系数DataFrame矩阵表格。

def pearson_corr(df):
    user_df = df.loc[df['carduser_id']== 2085728 ].reset_index(drop=True)
    relat = user_df[['volumn','amount']]
    pearson = relat.corr(method='pearson',min_periods=1)
    pv = round((pearson['amount'].values)[0],4)    
    
    return pv

pv = pearson_corr(trade_df)
print(pv)

0.9489

4. 归一化、标准化

现实的数据一般都是有单位的，比如常用身高的单位有米、厘米，这些情况会影响到数据分析的结果，这个无量纲化并不是说统一量纲为米，而是说，无论是米还是厘米，最后都会变成1，也就是没有了单位。无量纲化使不同规格的数据转换到同一规格。常见的无量纲化方法有标准化和归一化。

标准化（Z-Score）

$\\frac{x_{i}- \\mu }{\\sigma}$
其中：

$x^{'}$ —新值
$x_{i}$ —输入值（原始值）
$\\mu$ 和 $\\sigma$ 表示 $X_{i}$ 均值和标准差。

最大、最小值归一化（缩放）

以上是关于Pandas高级数据分析快速入门之五——机器学习特征工程篇的主要内容，如果未能解决你的问题，请参考以下文章

Pandas高级数据分析快速入门之六——机器学习预测分析篇

Pandas高级数据分析快速入门之二——基础篇

Pandas高级数据分析快速入门之四——数据可视化篇

Pandas高级数据分析快速入门之一——Python开发环境篇

Pandas高级数据分析快速入门之三——数据挖掘与统计分析篇

机器学习入门实战加州房价预测