《重学数据结构》之什么是二叉树？

Posted 2021-09-21 JavaEdge.

基本概念

树，一种非线性表数据结构：

• 节点
  “树”里面的每个元素
• 父子关系
  连线相邻节点之间的关系
• 兄弟节点
  节点的父节点是同一个节点
• 根节点
  没有父节点的节点
• 叶（子）节点
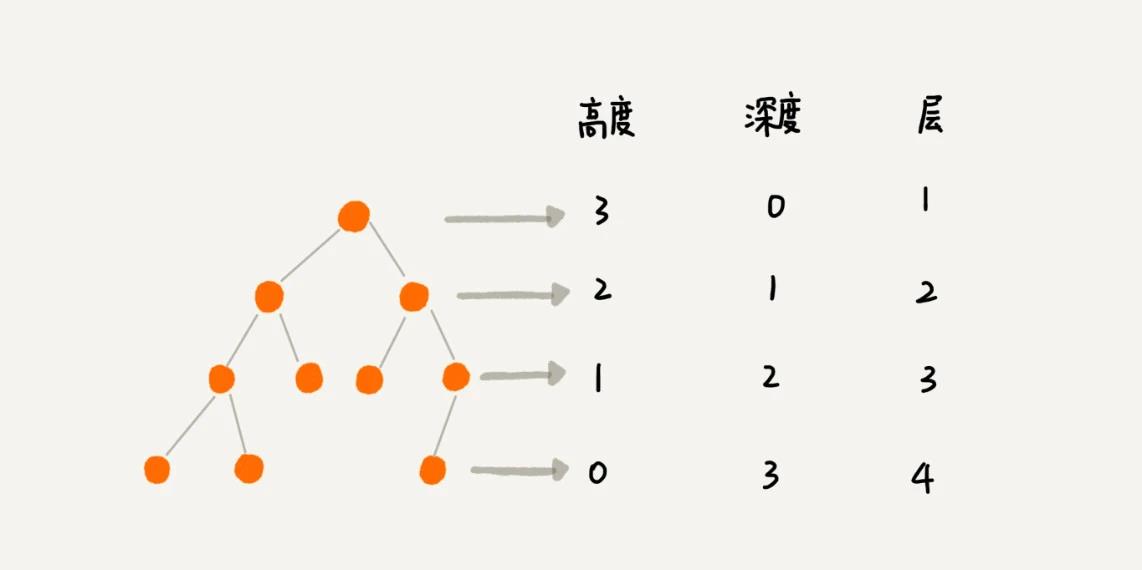
  没有子节点的节点
• 节点的高度
  节点到叶节点的最长路径(边数)
• 树的高度
  根节点的高度
• 节点的深度
  根节点到该节点所经历的边的个数
• 节点的层数
  节点的深度+1
  

二叉树（Binary Tree）

最常用的树结构。

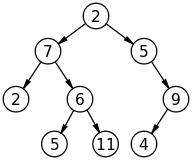
每个节点最多有两个子节点：左子节点，右子节点。

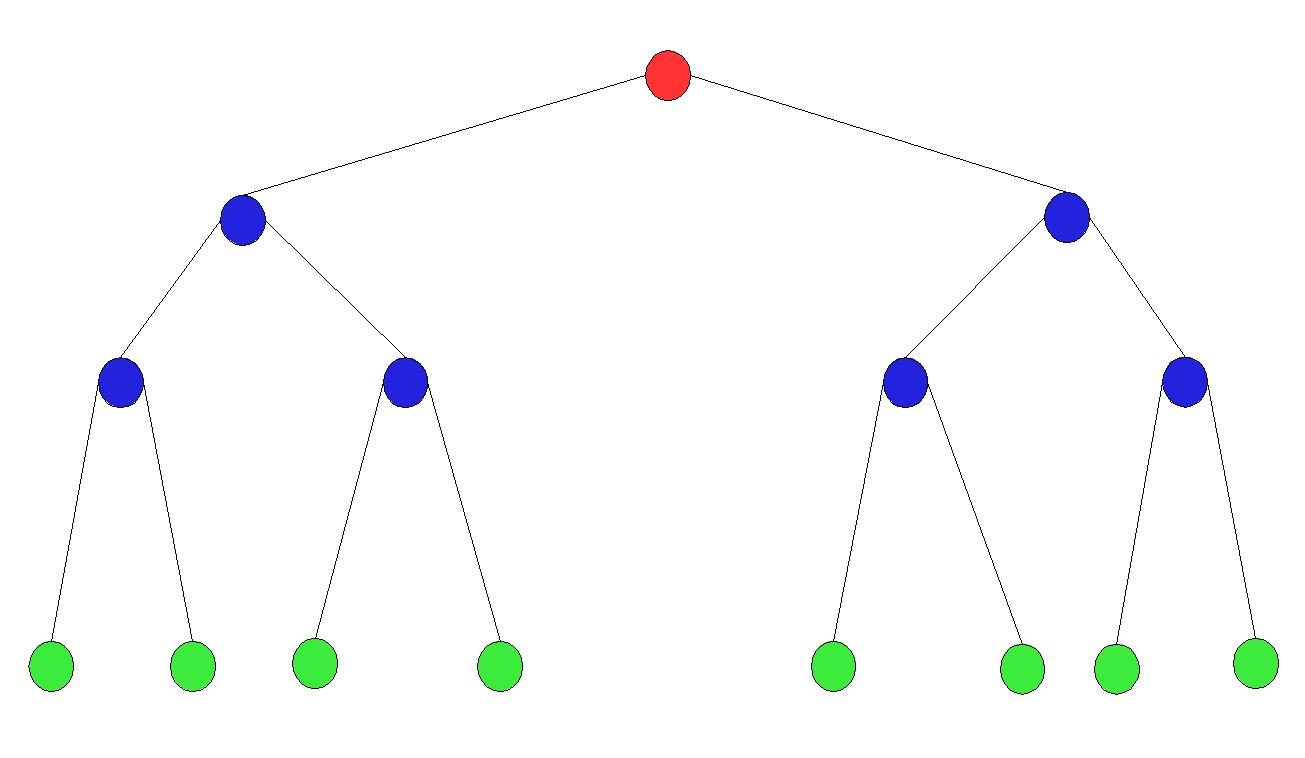
• 满二叉树
  叶节点全在最底层，除叶节点外，每个节点都有左右两个子节点
  
• 完全二叉树
  叶节点都在最底下两层，最后一层的叶节点都靠左排列，且除最后一层，其他层节点个数都达到最大

为啥就把最后一层的叶子节点靠左排列的叫完全二叉树？靠右排列为啥就不行？

要搞清楚完全二叉树为啥这么定义，先学习

如何存储二叉树？

基于指针或者引用的二叉链式存储法

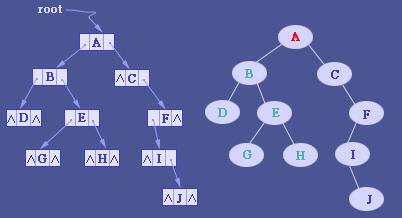
每个节点有三个字段：

• 一个存储数据
• 另两个指向左右子节点的指针

大部分二叉树代码都是通过这种结构实现的。

基于数组的顺序存储法

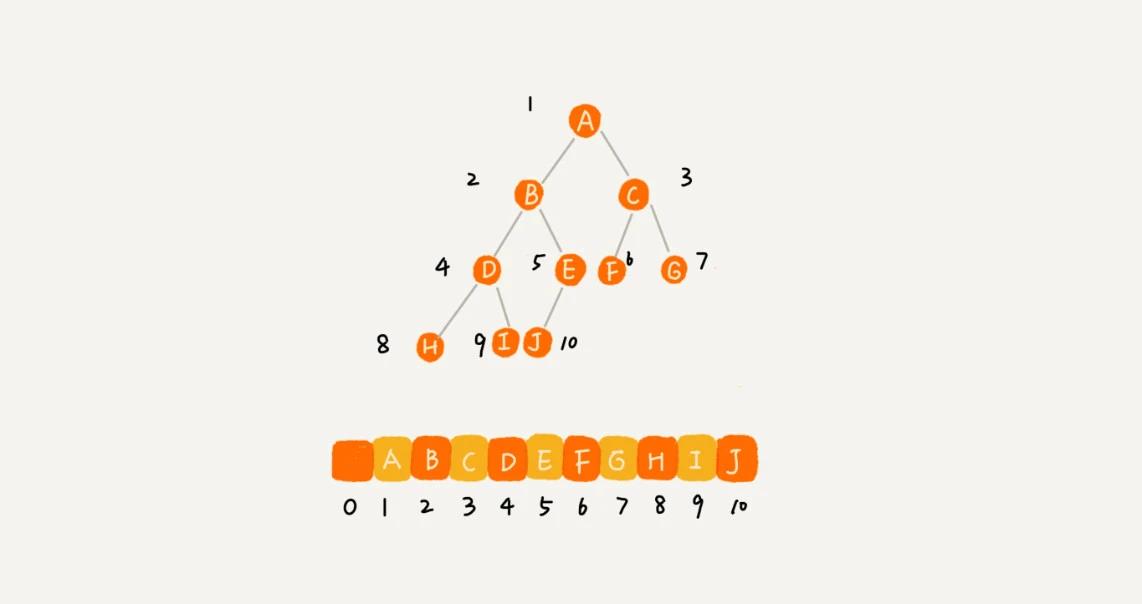
若节点X存储在数组中下标为i的位置
2 * i 存储左子节点
2 * i + 1存储右子节点
i/2存储其父节点

由于这是个完全二叉树，所以仅“浪费”了一个下标0的存储位置。若是非完全二叉树，就会浪费较多存储空间：

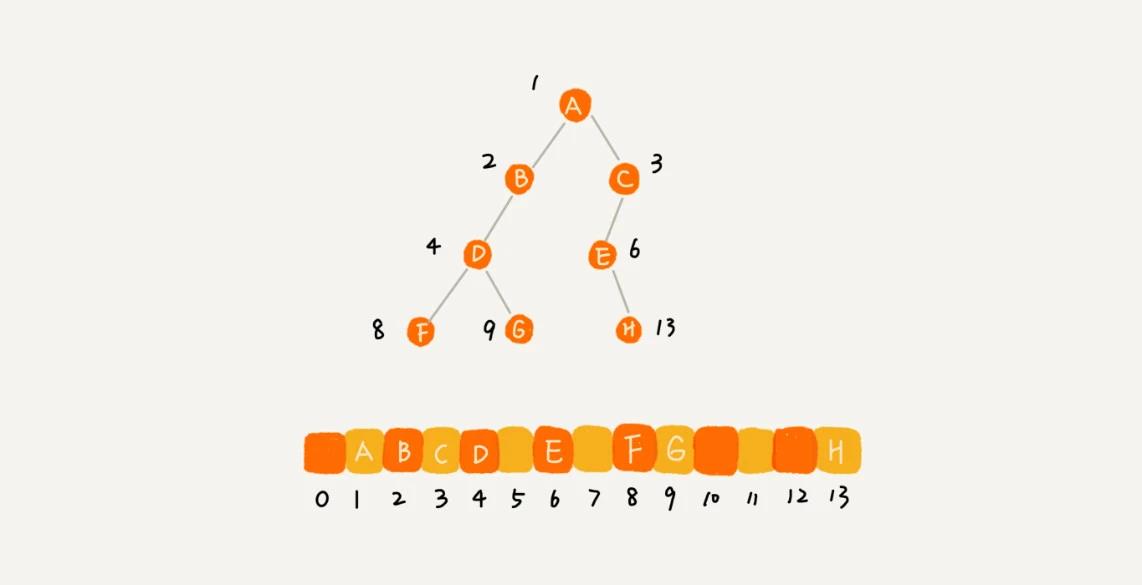
所以完全二叉树用数组存储最省内存，就不像链式存储法，还要存储左、右子节点的指针。所以完全二叉树要求最后一层的子节点都靠左。

堆也是一种完全二叉树，所以其最常用的存储方式就是数组。

二叉树的遍历

经典遍历

• 前序遍历
  对于树中的任意节点来说，先打印这个节点，然后再打印它的左子树，最后打印它的右子树。
• 中序遍历
  对于树中的任意节点来说，先打印它的左子树，然后再打印它本身，最后打印它的右子树。
• 后序遍历
  对于树中的任意节点来说，先打印它的左子树，然后再打印它的右子树，最后打印这个节点本身。
  
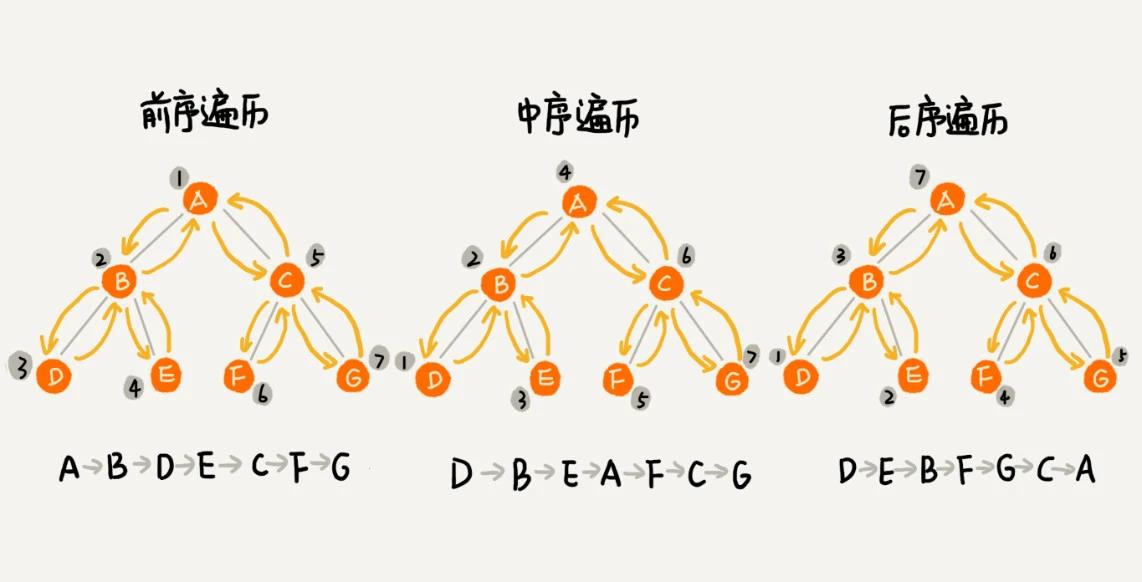
  这些都是递归过程。

递归代码的关键就是递推公式，递推公式的关键就是，如果要解决问题A，就假设子问题B、C已经解决，然后再来看如何利用B、C来解决A。

所以可以写出前、中、后序遍历的

递推公式

前序遍历

preOrder(r) = print r->preOrder(r->left)->preOrder(r->right)

中序遍历

inOrder(r) = inOrder(r->left)->print r->inOrder(r->right)

后序遍历

postOrder(r) = postOrder(r->left)->postOrder(r->right)->print r

void preOrder(Node* root) {
  if (root == null) return;
  print root // 此处为伪代码，表示打印root节点
  preOrder(root->left);
  preOrder(root->right);
}

void inOrder(Node* root) {
  if (root == null) return;
  inOrder(root->left);
  print root // 此处为伪代码，表示打印root节点
  inOrder(root->right);
}

void postOrder(Node* root) {
  if (root == null) return;
  postOrder(root->left);
  postOrder(root->right);
  print root // 此处为伪代码，表示打印root节点
}

时间复杂度

每个节点最多会被访问两次，所以遍历操作的时间复杂度，跟节点的个数n成正比，也就是说二叉树遍历的时间复杂度是O(n)。

参考

• https://zh.wikipedia.org/wiki/%E4%BA%8C%E5%8F%89%E6%A0%91