夜深人静写算法（四十）- 八大排序

Posted 2021-09-20 英雄哪里出来

目录 零、算法概述 一、冒泡排序 二、选择排序 三、插入排序 四、希尔排序 五、归并排序 六、快速排序 七、计数排序 八、基数快速    

零、算法概述   本章主要讲的内容是通过一些动图，学会 「 八大排序 」 算法。各个排序算法中的思想都非常经典，如果能够一一消化，那么在学习算法的路上也会轻松许多。
  从 「 冒泡排序 」中，我们会利用数据交换这个算法； 「 选择排序 」中，我们将学会从一个数组中找最大值； 「 插入排序 」中，我们将学会对一个有序数组执行插入到对应位置的操作； 「 希尔排序 」，让我们了解了增量的强大性； 「 归并排序 」中，让我们了解了如何利用两个有序数组进行合并； 「 快速排序 」，很快！ 「 计数排序 」，利用了哈希表的思想； 「 基数排序 」 中，引入了桶的概念。

一、冒泡排序  

图示	含义
■ 的柱形	代表尚未排好序的数
■ 的柱形	代表正在执行比较的两个数
■ 的柱形	代表已经排好序的数

  我们看到，首先需要将 「第一个元素」 和 「第二个元素」 进行 「比较」，如果 前者 大于 后者，则进行 「交换」，然后再比较 「第二个元素」 和 「第三个元素」 ，以此类推，直到 「最大的那个元素」 被移动到 「最后的位置」 。
  然后，进行第二轮「比较」，直到 「次大的那个元素」 被移动到 「倒数第二的位置」 。
  最后，经过一定轮次的「比较」 和 「交换」之后，一定可以保证所有元素都是 「升序」 排列的。

---

二、选择排序  

图示	含义
■ 的柱形	代表尚未排好序的数
■ 的柱形	代表正在执行 比较 的数
■ 的柱形	代表已经排好序的数
■ 的柱形	有两种：1、记录最小元素 2、执行交换的元素

  我们发现，首先从 「第一个元素」 到 「最后一个元素」 中选择出一个 「最小的元素」，和 「第一个元素」 进行 「交换」；
  然后，从 「第二个元素」 到 「最后一个元素」 中选择出一个 「最小的元素」，和 「第二个元素」 进行 「交换」。
  最后，一定可以保证所有元素都是 「升序」 排列的。

---

三、插入排序  

图示	含义
■ 的柱形	代表尚未排好序的数
■ 的柱形	代表正在执行 比较 和 移动 的数
■ 的柱形	代表已经排好序的数
■ 的柱形	代表待执行插入的数

  我们看到，首先需要将 「第二个元素」 和 「第一个元素」 进行 「比较」，如果 前者 小于等于 后者，则将 后者 进行向后 「移动」，前者 则执行插入；
  然后，进行第二轮「比较」，即 「第三个元素」 和 「第二个元素」、「第一个元素」 进行 「比较」， 直到 「前三个元素」 保持有序 。
  最后，经过一定轮次的「比较」 和 「移动」之后，一定可以保证所有元素都是 「升序」 排列的。

---

四、希尔排序  

  一下子看完不是很理解，没有关系，我们把这几个过程分拆开来。第一趟分解后，如图所示：


  增量为 4，所有元素总共分为 4 组，分别为 [8, 3]、[5, 7]、[6, 10]、[4, 2]，同组内部分别执行插入排序，得到 [3, 8]、[5, 7]、[6, 10]、[2, 4]（由于每组只有两个元素，所以升序的情况位置不变，降序的情况执行组内元素位置交换，抖动一下代表保持原顺序不变，有一种 “我不换 ~~ 我不换” 的意思在里面 ）。

  第二趟分解后，如图所示：


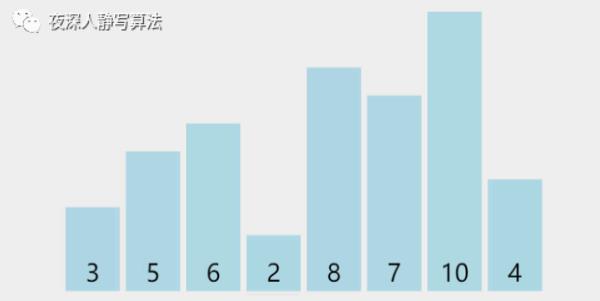
  增量为 2，所有元素总共分为 2 组，分别为 [3, 6, 8, 10]、[5, 2, 7, 4]，同组内部分别执行插入排序，[3, 6, 8, 10]已经升序，保持原样；[5, 2, 7, 4] 执行三次插入排序后变成 [2, 4, 5, 7]。
  第三趟分解后，如图所示：


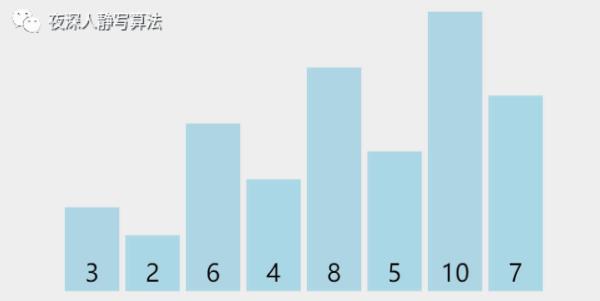
  增量为 1，所有元素归为 1 组，为 [3, 2, 6, 4, 8, 5, 10, 7]。对它执行简单插入排序，执行完毕后，必然可以保证所有元素有序。

---

五、归并排序  

图示	含义
■ 的柱形	代表尚未排好序的数
■ 的柱形	代表已经排好序的数
其他颜色 ■ 的柱形	正在递归、归并中的数

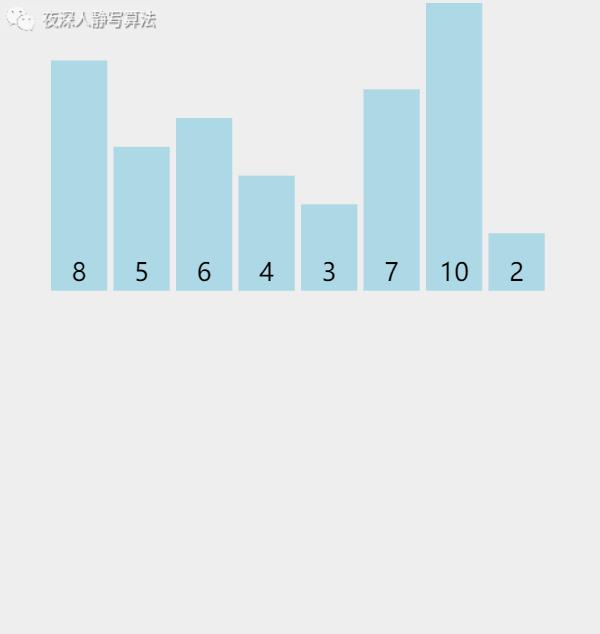
  我们发现，首先将 「 8个元素 」 分成 「 4个元素 」，再将 「 4个元素 」 分成 「 2个元素 」，然后 「比较」这「 2个元素 」的值，使其在自己的原地数组内有序，然后两个 「 2个元素 」 的数组归并变成 「 4个元素 」 的 「升序」数组，再将两个「 4个元素 」 的数组归并变成 「 8个元素 」 的 「升序」数组。

---

六、快速排序  

图示	含义
■ 的柱形	代表尚未排好序的数
■ 的柱形	代表随机选定的基准数
■ 的柱形	代表已经排序好的数
■ 的柱形	代表正在遍历比较的数
■ 的柱形	代表比基准数小的数
■ 的柱形	代表比基准数大的数

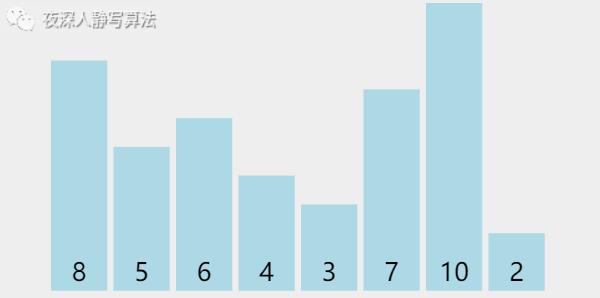
  我们发现，首先随机选择了一个 7 作为「 基准数 」，并且将它和最左边的数交换。然后往后依次遍历判断，小于 7 的数为 「 绿色 」 ，大于 7 的数为「 紫色 」，遍历完毕以后，将 7 和 「 下标最大的那个比 7 小的数 」交换位置，至此，7的左边位置上的数都小于它，右边位置上的数都大于它，左边和右边的数继续递归求解即可。

---

七、计数排序  

图示	含义
■ 的柱形	计数为 0 的数
■ 的柱形	计数为 1 的数
■ 的柱形	计数为 2 的数
■ 的柱形	计数为 3 的数
■ 的柱形	计数为 4 的数

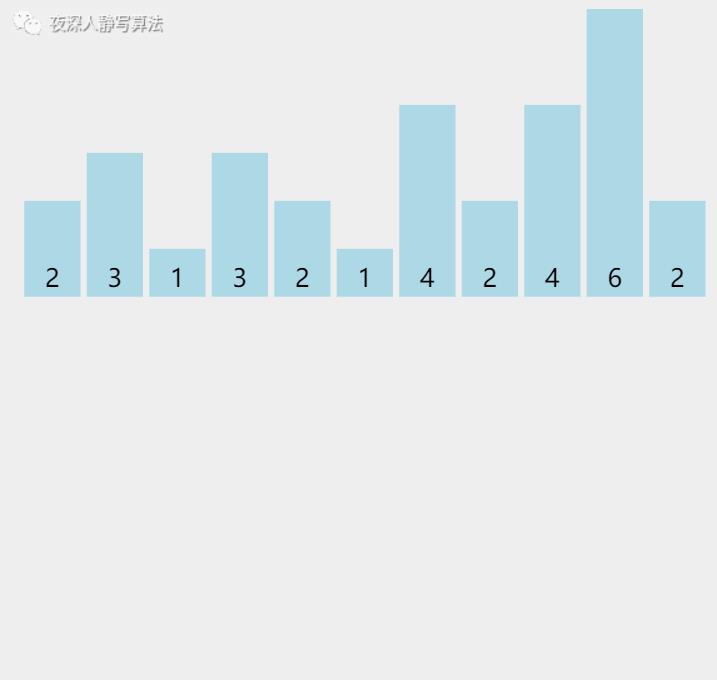
  我们看到，首先程序生成了一个区间范围为 $[1,9]$ 的 「 计数器数组 」，并且一开始所有值的计数都为 0。
  然后，遍历枚举「 原数组 」的所有元素，在 元素值 对应的计数器上执行 「 计数 」 操作。
  最后，遍历枚举「 计数器数组 」，按照数组中元素个数放回到 「 原数组 」 中。这样，一定可以保证所有元素都是 「升序」 排列的。

---

八、基数排序  

「 红色的数字位 」 代表需要进行 「 哈希 」 映射到给定 「 队列 」 中的数字位。
  我们看到，首先程序生成了一个区间范围为 $[0,9]$ 的 「 基数队列 」。
  然后，总共进行了 4 轮「 迭代 」（因为最大的数总共 4 个数位）。
  每次迭代，遍历枚举 「 原数组 」 中的所有数，并且取得本次迭代对应位的数字，通过「 哈希 」，映射到它「 对应的队列 」中 。然后将 「 队列 」 中的数据按顺序塞回 「 原数组 」 完成一次「 迭代 」，4 次「 迭代 」后，一定可以保证所有元素都是 「升序」 排列的。

---

  冒泡排序： 不断迭代，每次迭代就把当前最大的元素往右边靠；
  选择排序： 不断迭代，每次迭代选择当前最小元素往左边靠；
  插入排序： 不断迭代，每次维护一个有序数组，并且将当前元素插入到有序数组合适位置；
  希尔排序： 枚举增量，对不同下标增量进行分组，分别执行插入排序，再减小增量重复执行；
  归并排序： 每次将数组分成长度接近的两部分，分别执行归并排序后，进行合并，再回溯；
  快速排序： 选择一个基点，比基点小的元素到它左边，比基点大的元素到它右边，分别对两堆递归执行快速排序；
  计数排序： 一次遍历，将所有数组映射到哈希表中，再遍历哈希表进行输出；
  基数排序： 从最低的位开始映射到 0 - 9 的桶，利用计数排序思想，让最低位先保证有序。再处理次低位，直到最高位处理完毕后，数组有序；

---

• 有关🌳《排序》🌳 的源码均开源，链接如下：《八大排序》
• 如果还有不懂的问题，可以 通过主页 找到作者的微信进行在线咨询。

---