进一步理解平衡二叉树(插入)

Posted 2021-09-20 两片空白

目录

前言

一.平衡二叉树的概念

 二.平衡二叉树的实现

 2.1 平衡二叉树结点的定义

 2.2 平衡二叉树的插入

        2.2.1按照二叉搜索树的方式插入新结点

                2.2.2 更新平衡因子

                2.2.3 旋转 

 2.3 平衡二叉树的验证

 2.4 总代码

 2.5 平衡二叉树的删除

---

前言

        前面我们了解了二叉搜索树，也进行了对二叉搜索树的简单实现。但是二叉搜索树存在一个缺陷。

        当要在搜索树里插入或者删除数据时，都需要进行查找。查找体现了搜索树的效率。当插入二叉树搜索树的集合是一个有序序列时，二叉搜索树会形成一个单支树。变成一个链状结构，这样查找的效率大大降低，最坏情况下，查找的效率为O(N)。并没有很好的体现出搜索树的性质。

        而平衡二叉树就很好的体现出了搜索树的性质，查找的效率是树的高度次，最坏的情况下查找的效率是O(logN)。

        下面就来详细介绍是如何实现平衡二叉树的。

一.平衡二叉树的概念

        首先一颗平衡二叉树必须是一颗二叉搜索树。二叉树搜索树的所有性质都符合平衡二叉树。另外平衡二叉树还具有一下性质：

1. 左右子树的高度差(简称平衡因子)的绝对值不超过1(-1/0/1)。
2. 左右子树也都是平衡二叉树。

这里引出来一个平衡因子的概念：平衡因子是平衡二叉树的高度差。

        计算公式为：平衡因子 = 右子树子树的高度 - 左子树子树的高度。(注意是子树的高度)

例如：

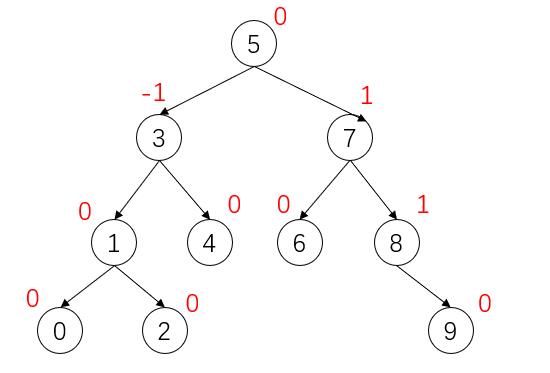
        根据上面的概念，如果一颗二叉搜索树是高度平衡的，即平衡因子绝对值小于等于1，这棵树就是平衡二叉树。如果右n个结点，搜索时的时间复杂度就是O(logN)。

 二.平衡二叉树的实现

        2.1 平衡二叉树结点的定义

//二叉树应用KV模型
template<class K, class V>
struct AVLTreeNode
{
	AVLTreeNode(const pair<K, V> kv)
	:_left(nullptr)
	, _right(nullptr)
	, _parent(nullptr)
	,_bf(0)
	, _kv(kv)
	{}

	AVLTreeNode *_left;//该节点的左孩子
	AVLTreeNode *_right;//该节点的右孩子
	AVLTreeNode *_parent;//该节点的父亲
	//平衡因子
	int _bf;
	//保存的是键值对，pair结构体
	pair<K, V> _kv;
};

 实现的这颗平衡二叉树是KV模型的，二叉树是按照键值对<key,value>的键值key来建树的，一个键值key对应一个value。

每个结点了处理右左右结点指针和键值对外，还增加了父指针和平衡因子。父指针是为了更方便更新平衡因子，平衡因子是用来判断该节点是否平衡。

注意平衡因子不是必须的，可以直接求结点左右子树的高度，在求差值。

        2.2 平衡二叉树的插入

         平衡二叉树也是一颗二叉搜索树，插入也要利用二叉搜索树的性质进行插入。只是需要在此基础上还需要更新结点的平衡因子，检测结点的平衡因子，遇到不符合条件的需要旋转处理。

        所以要实现平衡二叉树的插入步骤是：

1. 按照二叉搜索树的方式插入新节点
2. 更新结点的平衡因子。更新完该节点的平衡因子后，需要检测该节点的平衡因子。如果平衡因子绝对值小于等于1，再判断是否需要继续往上更新结点平衡因子。如果平衡因子绝对值大于等于2，旋转处理。

        2.2.1按照二叉搜索树的方式插入新结点

        这个只需要按照二叉搜索树的性质，如果插入结点的键值key大于当前结点键值，往右子树走，如果插入结点的键值key小于当前结点的键值，往左子树走。如果插入结点的键值key等于当前结点键值，说明已存在，插入失败。

        注意：插入结点是以叶子结点插入的。还要注意更新父节点。

        //空结点，根节点就是新插入结点
        if (_root == nullptr){
			_root = new Node(kv);
			return true;
		}
		Node *cur = _root;
		Node *parent = nullptr;
		while (cur)
		{
			if (kv.first > cur->_kv.first){
				parent = cur;
				cur = cur->_right;
			}
			else if (kv.first < cur->_kv.first){
				parent = cur;
				cur = cur->_left;
			}
			else{
				return false;
			}
		}
		//找到插入位置，现在进行插入
		cur = new Node(kv);
		//要更新父节点
		cur->_parent = parent;
        //判断插入父节点的左边还是右边
		if (parent->_kv.first < kv.first){
			
			parent->_right = cur;
		}
		else{
			
			parent->_left = cur;
		}

  2.2.2 更新平衡因子

        注意：插入一个结点，只会影响当前结点父节点，或者说是祖先结点的平衡因子。但是并不会影响全部的父节点或者祖先结点。所以更新平衡因子从下往上更新。

比如说：

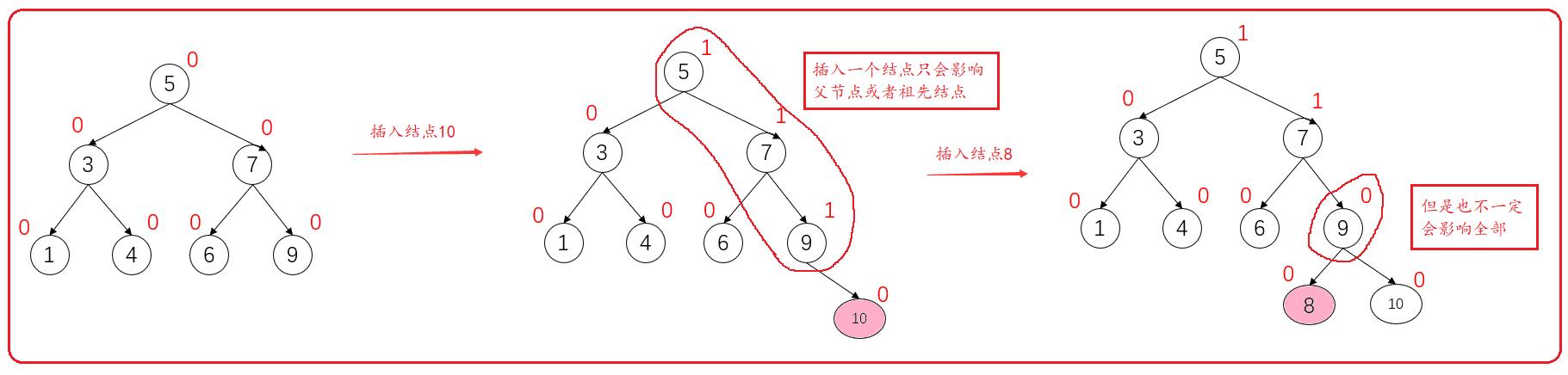
•  如何更新平衡因子呢？

        在结点更新时，是从插入节点一直向父节点更新的。从下往上更新。

如图：

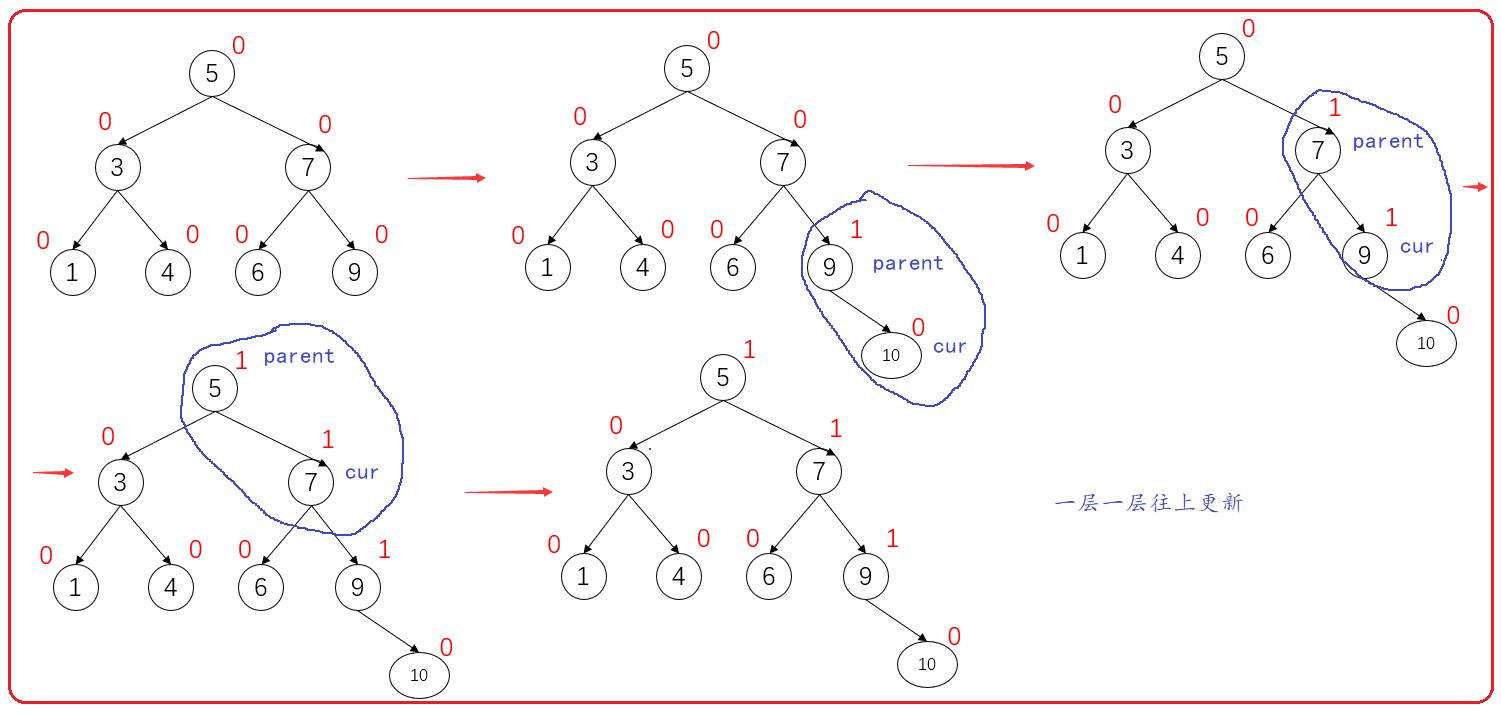
         由平衡因子的定义，由上图，我们可以得到。

        当cur是parent的左节点时，parent的平衡因子减1，

        当cur是parent的右节点时，parent的平衡因子加1。

• 检测更新完结点的平衡因子

        更新完的平衡因子会有一下三种情况。

1. 更新完后，结点(parent结点)的平衡因子等于0。说明结点(parent结点)的高度没有变化，并不会对上面结点的平衡因子产生影响。不需要继续往上更新。
2. 更新完后，结点(parent结点)的平衡因子等于1或者-1。说明当前结点(parent结点)高度加1了，但是还没有超过平衡的界限，会对上面的结点产生影响。继续往上更新。
3. 更新完后，结点(parent结点)的平衡因子等于2或者-2。超过了平衡的界限，需要进行旋转处理。

由于旋转后平衡因子会在界限范围内，所以只有上面三种情况。

2.2.3 旋转 

旋转要注意两点，一点是旋转完后仍然是搜索树，二是每个结点都需要平衡。

 平衡二叉树的旋转有四种情况：

• 右单旋

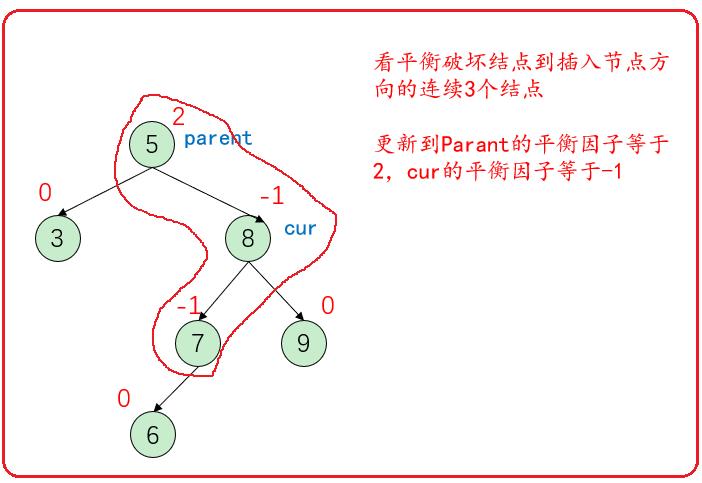
在什么情况下使用右单旋？

        看平衡破坏结点到插入方向的连续3个结点，如果是一条直线用单旋，如果更新到parent结点的平衡因子等于-2，且cur的平衡因子等于-1时，需要用右单旋。

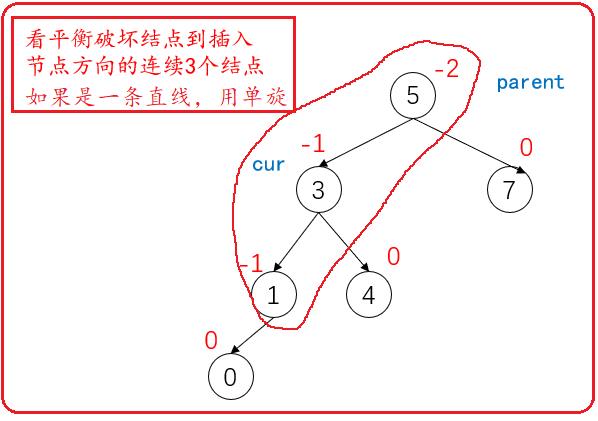
 怎样实现右单旋？

情况是这样的：所有右单旋情况都适用

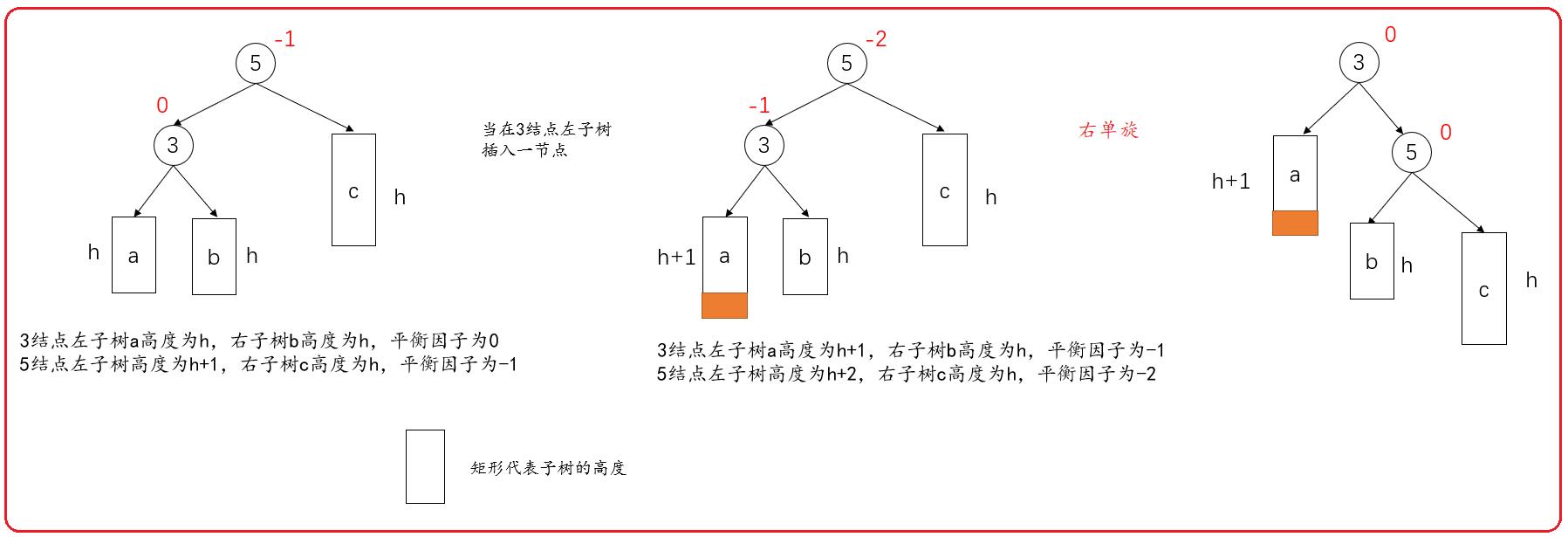
        根据上图，我们知道，右单旋是将结点5的左指针指向结点3的右子树，结点3的右指针指向结点5。

为什么将结点5的左指针指向结点3的右子树？

为了保持树是搜索树，结点3的右结点值大于3，小于5，右单旋后，需要结点3的右指针指向结点5，所以需要将结点5的左指针指向结点3的右子树。

但是不仅仅是这么简单，还需要更新父节点和平衡因子。我们发现此时受影响结点的平衡因子都是0。

在旋转过程中还需要几种情况需要考虑：

1. 结点3的右子树可能是空树，也可能不是空树
2. 结点5可能是根节点。也可能上面还有父节点，是一颗子树。如果是根节点，要更新根节点。如果是子树，可能是某个节点的左子树或者右子树。

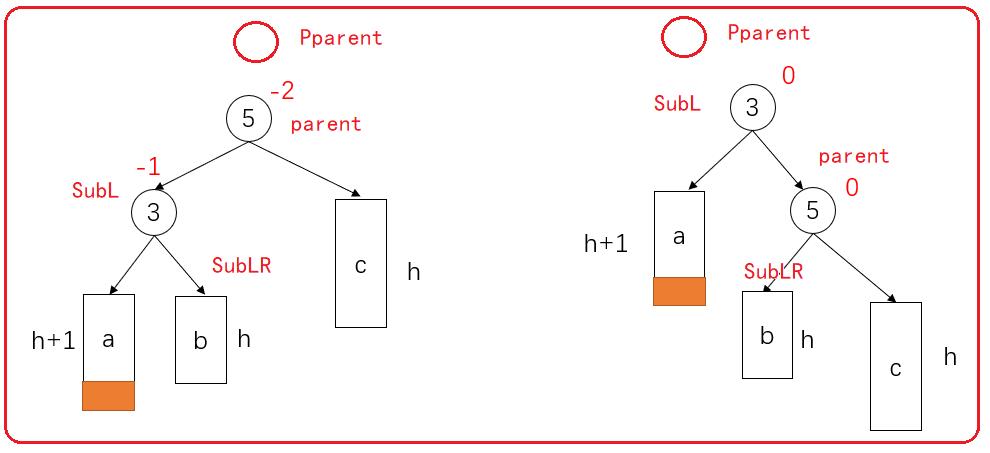
	void SigelRight(Node *parent){
        //先将所有要用到的结点记录
		Node *SubL = parent->_left;
		Node *SubLR = SubL->_right;

		Node *Pparent = parent->_parent;
        //更新SubLR结点
		parent->_left = SubLR;
        //注意可能为空的情况
		if (SubLR){
			SubLR->_parent = parent;
		}
        //更新parent
		SubL->_right = parent;
		parent->_parent = SubL;
        
		if (Pparent == nullptr)//根节点，不是子树
		{
			
			SubL->_parent = nullptr;
            //更新根节点
			_root = SubL;
		}
		else//子树
		{
            //判断插入左边还是右边
			if (Pparent->_kv.first > SubL->_kv.first){
				Pparent->_left = SubL;
			}
			else{
				Pparent->_right = SubL;
			}
			SubL->_parent = Pparent;
		}
        //更新平衡因子
		SubL->_bf = 0;
		parent->_bf = 0;
	}

• 左单旋

在什么情况下使用左单旋？

        看平衡破坏结点到插入方向的连续3个结点，如果是一条直线用单旋。如果更新到parent结点的平衡因子等于2，且cur的平衡因子等于1时，需要用左单旋。

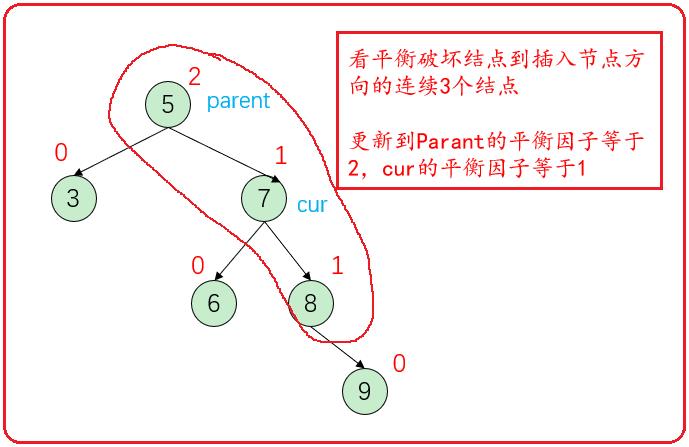
 怎么实现左单旋？

        左单旋的实现和右单旋转的实现异曲同工，只是方向不同。

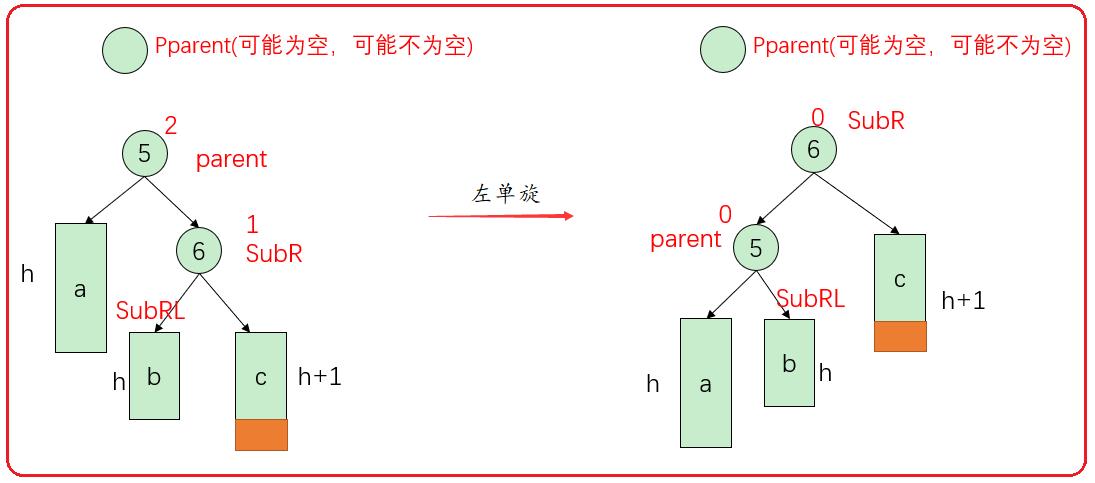
情况如下：一般化(适用所有情况)

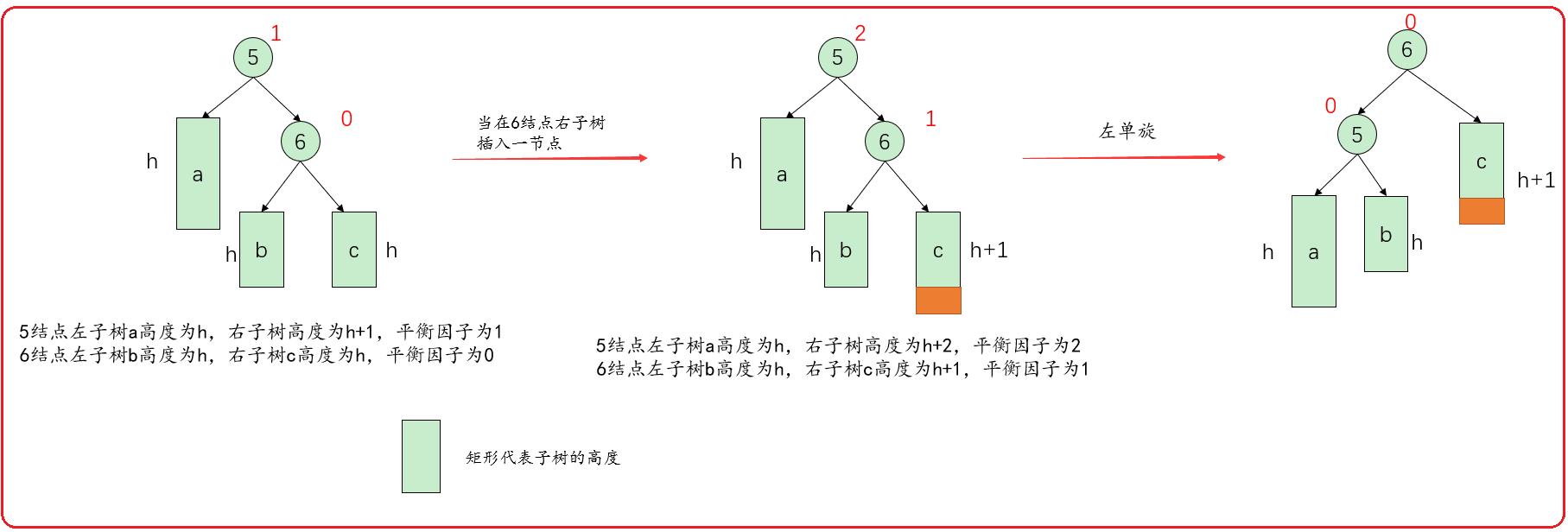
  根据上图，我们知道，左单旋是将结点5的右指针指向结点6的左子树，结点6的左指针指向结点5。

为什么结点5的右指针指向结点6的左子树？

因为平衡二叉树仍然是一颗搜索树，结点6的左结点值小于6，大于5，左单旋后，需要结点6的左指针指向结点5，所以需要将结点5的右指针指向结点6的左子树。

注意更新父指针和平衡因子。我们发现此时受影响结点的平衡因子都是0。

在旋转过程中还需要几种情况需要考虑：

1. 结点6的左子树可能是空树，也可能不是空树
2. 结点5可能是根节点。也可能上面还有父节点，是一颗子树。如果是根节点，要更新根节点。如果是子树，可能是某个节点的左子树或者右子树。

void SigelLeft(Node *parent){
		//保持所有用到的结点
		Node *SubR = parent->_right;
		Node *SubRL = SubR->_left;
		//用来判断当前子树是否是子树
		Node *Pparent = parent->_parent;
		//注意要更新父节点
		parent->_right = SubRL;
		//
		if (SubRL){
			SubRL->_parent = parent;
		}

		SubR->_left = parent;
		parent->_parent = SubR;

		//更新新根节点SubR的父节点
		if (Pparent == nullptr){//当前结点为根节点
			//直接置空
			SubR->_parent = nullptr;
			//注意要更新根节点
			_root = SubR;
		}
		else{//当前树为子树
			//连接到上面结点
			if (Pparent->_kv.first < SubR->_kv.first){
				Pparent->_right = SubR;
				
			}
			else{
				Pparent->_left = SubR;
			}

			//更新父节点
			SubR->_parent = Pparent;
		}
		//更新平衡因子
		SubR->_bf = 0;
		parent->_bf = 0;
	}

•  右左双旋

什么情况下用右左双旋？

        看平衡破坏结点到插入方向的连续3个结点，如果是一条折线用双旋。更新完后当前结点(parent结点)的平衡因子等于2，右节点(cur结点)等于-1时，用右左双旋。

 怎么实现右左双旋？

这时有两种情况会导致平衡因子的更新不同

情况1：

在SubRL左子树插入结点

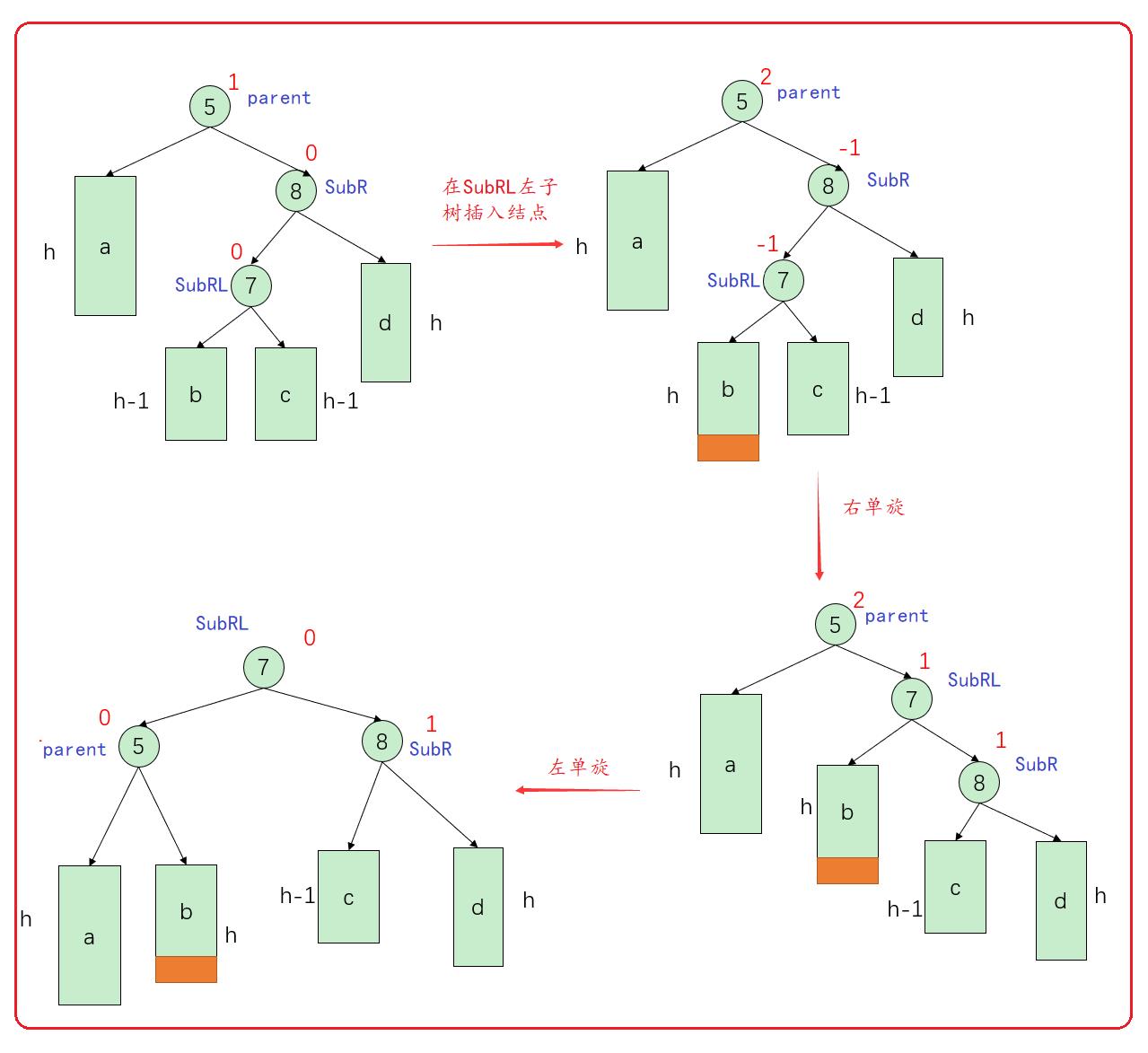
        通过上图，先将parent的右结点SubrR先右单旋，再将parent结点左单旋，即可得到平衡的二叉树。

        此时子树b，成为了parent的右子树，子树c成为了SubR的左子树，parent的平衡因子等于0 ，SubR的平衡因子等于1。

情况二：

在SubRL右子树插入结点

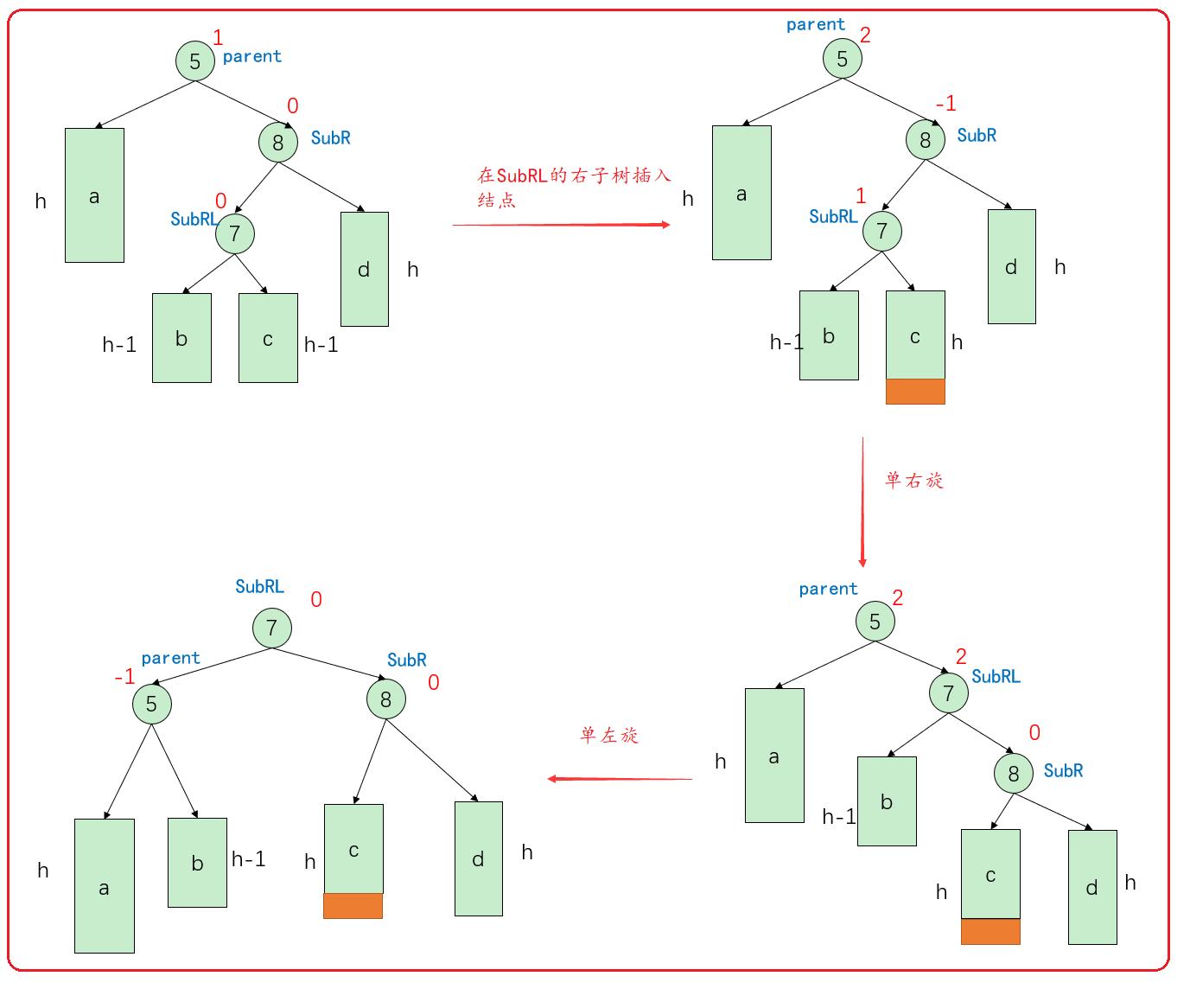
         通过上图，先将parent的右结点SubR先右单旋，再将parent结点左单旋，即可得到平衡的二叉树。

        此时子树b，成为了parent的右子树，子树c成为了SubR的左子树，parent的平衡因子等于-1 ，SubR的平衡因子等于0。

总结：

        右左双旋：先将parent的右子树右单旋，再将parent所在子树左单旋。

        当插入结点在SubRL的左子树时SubRL平衡因子为-1时：parent的平衡因子等于0 ，SubR的平衡因子等于1。

        当插入结点在SubRL的右子树SubRL平衡因子为1时：parent的平衡因子等于-1 ，SubR的平衡因子等于0。

void DoubleRightLeft(Node *parent){
		Node *SubR = parent->_right;
		Node *SubRL = SubR->_left;

		//为了后面更新平衡因子，看插入左边还是右边
		int bf = SubRL->_bf;

		SigelRight(SubR);

		SigelLeft(parent);
		//画图理解,更新平衡因子
		if (bf == 1){//插入方向在右边
			SubR->_bf = 0;
			SubRL->_bf = 0;
			parent->_bf = -1;
		}
		else if (bf == -1){//插入方向在左边
			SubRL ->_bf= 0;
			parent->_bf = 0;
			SubR->_bf = 1;
		}
		else if (bf == 0){//SubRL就是插入结点
			SubR->_bf = 0;
			SubRL->_bf = 0;
			parent->_bf = 0;
		}
	}

• 左右双旋

什么情况下用左右双旋？

        看平衡破坏结点到插入方向的连续3个结点，如果是一条折线用双旋。更新完后当前结点(parent结点)的平衡因子等于-2，右节点(cur结点)等于1时，用左右双旋。

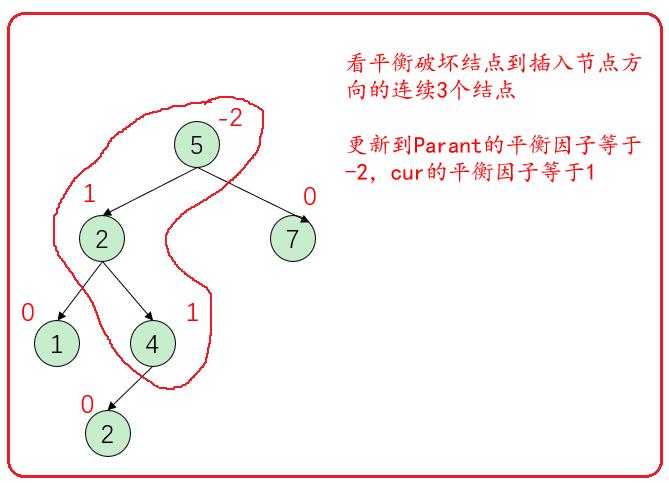
怎么实现左右双旋？

这时有两种情况会导致平衡因子的更新不同

情况1：

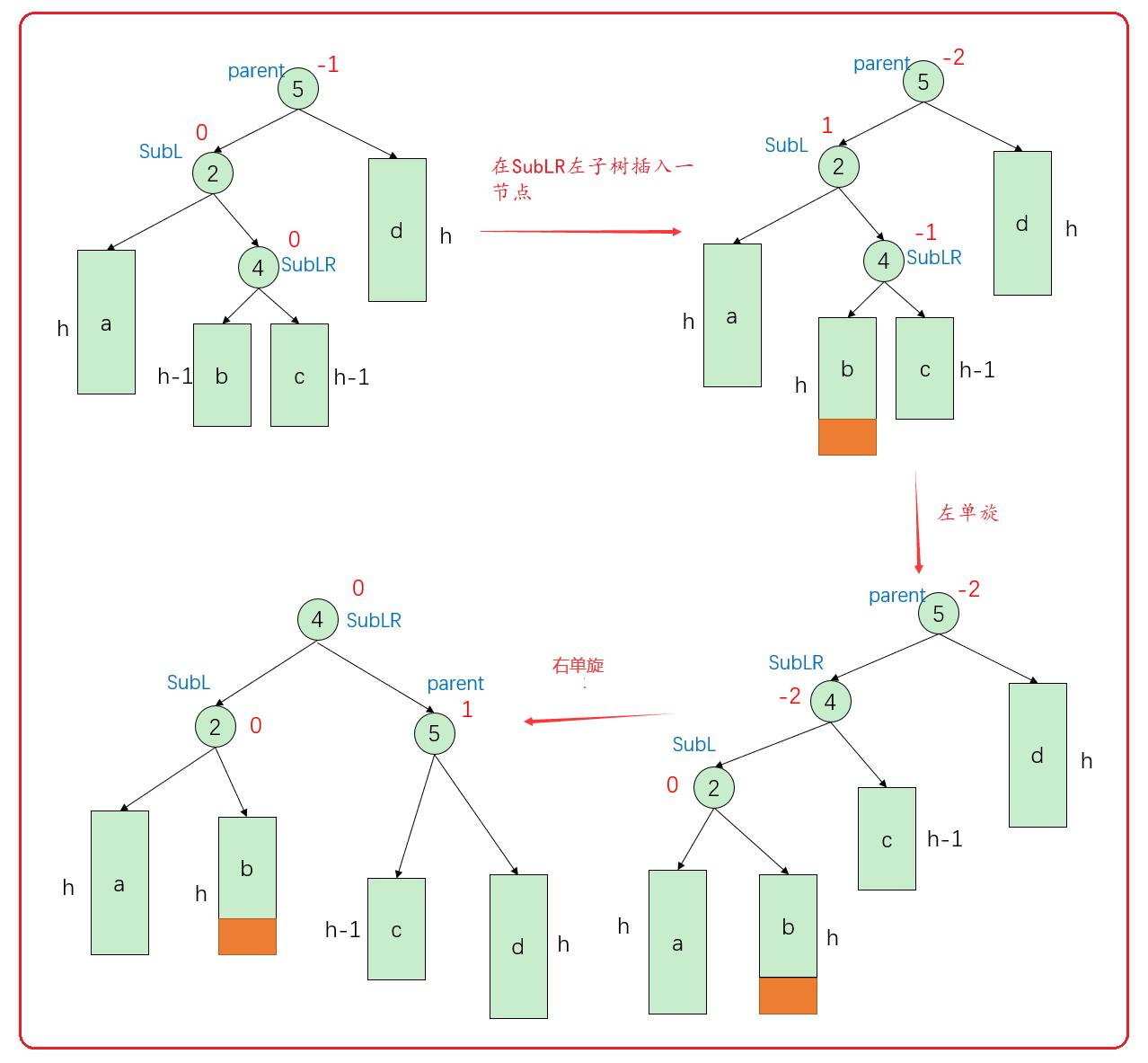
         通过上图，先将parent的左结点SubL先左单旋，再将parent结点右单旋，即可得到平衡的二叉树。

        此时子树b，成为了SubL的右子树，子树c成为了parent的左子树，parent的平衡因子等于1 ，SubL的平衡因子等于0。

情况二：

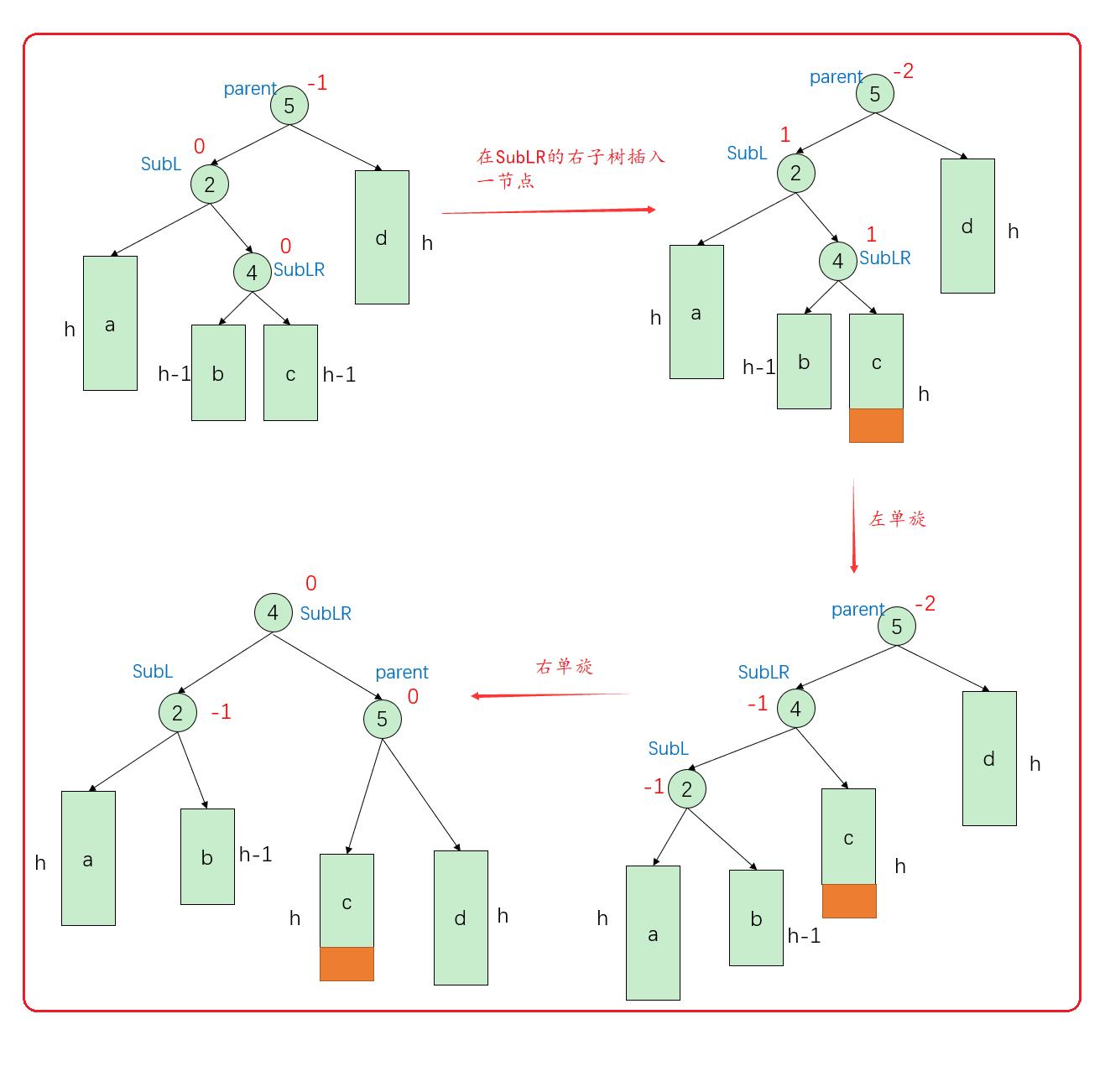
         通过上图，先将parent的左结点SubL先左单旋，再将parent结点右单旋，即可得到平衡的二叉树。

        此时子树b，成为了SubL的右子树，子树c成为了parent的左子树，parent的平衡因子等于0 ，SubL的平衡因子等于-1。

总结：

        左右单旋：先将parent的左结点所在子树左单旋，在将parent所在子树右单旋。

        当插入结点在SubLR的左子树时SubLR平衡因子为-1时：parent的平衡因子等于1，SubL的平衡因子等于0。

        当插入结点在SubLR的右子树SubLR平衡因子为1时：parent的平衡因子等于0 ，SubR的平衡因子等于-1。

void DoubleLeftRight(Node *parent){
		Node *SubL = parent->_left;
		Node *SubLR = SubL->_right;

		int bf = SubLR->_bf;

		SigelLeft(SubL);

		SigelRight(parent);

		if (bf == 1){
			SubL->_bf = -1;
			parent->_bf = 0;
			SubLR->_bf = 0;
		}
		else if (bf == -1){
			parent->_bf = 1;
			SubL->_bf = 0;
			SubLR->_bf = 0;
		}
		else if (bf == 0){
			parent->_bf = 0;
			SubL->_bf = 0;
			SubLR->_bf = 0;
		}
	}

 2.3 平衡二叉树的验证

• 每个结点的高度差(右子树高度-左子树高度)绝对值不超过1。
• 平衡因子等于高度差值。

    int _Height(Node *root){
		if (root == nullptr){
			return 0;
		}
		int left = _Height(root->_left);
		int right = _Height(root->_right);

		return left > right ? left + 1 : right + 1;
	}
    bool _IsBalanceTree(Node *pRoot)
	{

		// 空树也是AVL树
		if (nullptr == pRoot) 
            return true;

		// 计算pRoot节点的平衡因子：即pRoot左右子树的高度差
		int leftHeight = _Height(pRoot->_left);
		int rightHeight = _Height(pRoot->_right);
		int diff = rightHeight - leftHeight;

		// 如果计算出的平衡因子与pRoot的平衡因子不相等，或者
		// pRoot平衡因子的绝对值超过1，则一定不是AVL树
		if (diff != pRoot->_bf || (diff > 1 || diff < -1))
			return false;
		// pRoot的左和右如果都是AVL树，则该树一定是AVL树
		return _IsBalanceTree(pRoot->_left) && _IsBalanceTree(pRoot->_right);
	}

 2.4 总代码

#pragma once
#include<iostream>
using namespace std;

//二叉树应用KV模型
template<class K, class V>
struct AVLTreeNode
{
	AVLTreeNode(const pair<K, V> kv)
	:_left(nullptr)
	, _right(nullptr)
	, _parent(nullptr)
	,_bf(0)
	, _kv(kv)
	{}

	AVLTreeNode *_left;//该节点的左孩子
	AVLTreeNode *_right;//该节点的右孩子
	AVLTreeNode *_parent;//该节点的父亲
	//平衡因子
	int _bf;
	//保存的是键值对，pair结构体
	pair<K, V> _kv;
};

template<class K,class V>
class AVLTree
{
	typedef AVLTreeNode<K,V> Node;
public:
	bool insert(const pair<K, V> kv)
	{
		if (_root == nullptr){
			_root = new Node(kv);
			return true;
		}
		Node *cur = _root;
		Node *parent = nullptr;
		while (cur)
		{
			if (kv.first > cur->_kv.first){
				parent = cur;
				cur = cur->_right;
			}
			else if (kv.first < cur->_kv.first){
				parent = cur;
				cur = cur->_left;
			}
			else{
				return false;
			}
		}
		//找到插入位置，现在进行插入
		cur = new Node(kv);
		//要更新父节点
		cur->_parent = parent;
		if (parent->_kv.first < kv.first){
			
			parent->_right = cur;
		}
		else{
			
			parent->_left = cur;
		}

		//更新平衡因子
		while (parent){
			//如果插入左边平衡因子--
			if (parent->_left == cur){
				parent->_bf--;
			}
			//如果插入右边，平衡因子++
			else{
				parent->_bf++;
			}

			//判断平衡因子
			if (parent->_bf == 0){//如果parent位置平衡因子等于0，不再往上更新，高度没变
				break;
			}
			else if (parent->_bf == 1 || parent->_bf == -1){//高度变了，但是没有不平衡，继续往上更新
				cur = parent;
				parent = parent->_parent;
			}
			else if (parent->_bf == 2 || parent->_bf == -2){//不平衡需要旋转
				if (parent->_bf == 2 && cur->_bf == 1){
					SigelLeft(parent);//左单旋
				}
				else if (parent->_bf == 2 && cur->_bf == -1){
					DoubleRightLeft(parent);//右左双旋
				}
				else if (parent->_bf == -2 && cur->_bf == 1){
					DoubleLeftRight(parent);//左右双旋
				}
				else if (parent->_bf == -2 && cur->_bf == -1){
					SigelRight(parent);//右单旋
				}
				break;//旋转完不需要更新平衡因子了。

			}
			else{
				
			}
		}
		return true;


	}
	void SigelLeft(Node *parent){
		//保持所有用到的结点
		Node *SubR = parent->_right;
		Node *SubRL = SubR->_left;
		//用来判断当前子树是否是子树
		Node *Pparent = parent->_parent;
		//注意要更新父节点
		parent->_right = SubRL;
		//
		if (SubRL){
			SubRL->_parent = parent;
		}

		SubR->_left = parent;
		parent->_parent = SubR;

		//更新新根节点SubR的父节点
		if (Pparent == nullptr){//当前结点为根节点
			//直接置空
			SubR->_parent = nullptr;
			//注意要更新根节点
			_root = SubR;
		}
		else{//当前树为子树
			//连接到上面结点
			if (Pparent->_kv.first < SubR->_kv.first){
				Pparent->_right = SubR;
				
			}
			else{
				Pparent->_left = SubR;
			}

			//更新父节点
			SubR->_parent = Pparent;
		}
		//更新平衡因子
		SubR->_bf = 0;
		parent->_bf = 0;
	}

	void SigelRight(Node *parent){
		Node *SubL = parent->_left;
		Node *SubLR = SubL->_right;

		Node *Pparent = parent->_parent;

		parent->_left = SubLR;
		if (SubLR){
			SubLR->_parent = parent;
		}

		SubL->_right = parent;
		parent->_parent = SubL;

		if (Pparent == nullptr)//根节点
		{
			
			SubL->_parent = nullptr;
			_root = SubL;
		}
		else//子树
		{
			if (Pparent->_kv.first > SubL->_kv.first){
				Pparent->_left = SubL;
			}
			else{
				Pparent->_right = SubL;
			}
			SubL->_parent = Pparent;
		}

		SubL->_bf = 0;
		parent->_bf = 0;
	}

	void DoubleRightLeft(Node *parent){
		Node *SubR = parent->_right;
		Node *SubRL = SubR->_left;

		//为了后面更新平衡因子，看插入左边还是右边
		int bf = SubRL->_bf;

		SigelRight(SubR);

		SigelLeft(parent);
		//画图理解,更新平衡因子
		if (bf == 1){//插入方向在右边
			SubR->_bf = 0;
			SubRL->_bf = 0;
			parent->_bf = -1;
		}
		else if (bf == -1){//插入方向在左边
			SubRL ->_bf= 0;
			parent->_bf = 0;
			SubR->_bf = 1;
		}
		else if (bf == 0){//SubRL就是插入结点
			SubR->_bf = 0;
			SubRL->_bf = 0;
			parent->_bf = 0;
		}
	}

	void DoubleLeftRight(Node *parent){
		Node *SubL = parent->_left;
		Node *SubLR = SubL->_right;

		int bf = SubLR->_bf;

		SigelLeft(SubL);

		SigelRight(parent);

		if (bf == 1){
			SubL->_bf = -1;
			parent->_bf = 0;
			SubLR->_bf = 0;
		}
		else if (bf == -1){
			parent->_bf = 1;
			SubL->_bf = 0;
			SubLR->_bf = 0;
		}
		else if (bf == 0){
			parent->_bf = 0;
			SubL->_bf = 0;
			SubLR->_bf = 0;
		}
	}

	int _Height(Node *root){
		if (root == nullptr){
			return 0;
		}
		int left = _Height(root->_left);
		int right = _Height(root->_right);

		return left > right ? left + 1 : right + 1;
	}


	//int _Height(PNode pRoot);
	bool _IsBalanceTree(Node *pRoot)
	{


		// 空树也是AVL树
		if (nullptr == pRoot) return true;
		// 计算pRoot节点的平衡因子：即pRoot左右子树的高度差
		int leftHeight = _Height(pRoot->_left);
		int rightHeight = _Height(pRoot->_right);
		int diff = rightHeight - leftHeight;
		// 如果计算出的平衡因子与pRoot的平衡因子不相等，或者
		// pRoot平衡因子的绝对值超过1，则一定不是AVL树
		if (diff != pRoot->_bf || (diff > 1 || diff < -1))
			return false;
		// pRoot的左和右如果都是AVL树，则该树一定是AVL树
		return _IsBalanceTree(pRoot->_left) && _IsBalanceTree(pRoot->_right);
	}

	bool Isbalance(){
		return _IsBalanceTree(_root);
	}

private:
	Node *_root = nullptr;
};

 2.5 平衡二叉树的删除

        平衡二叉树的删除，和插入如出一辙。

        首先平衡二叉树也是二叉搜索树，也是先按照二叉搜索树的方式进行删除，然后更新平衡因子，判断平衡因子是否符合条件。

• 按照二叉搜索树的方式进行删除
• 更新平衡因子，判断平衡因子。如果符合条件，在判断是否继续往上更新，如果不符合，旋转处理。

和插入不同的是，更新平衡因子时，

        parent->_left==cur时，parent->_bf++

        parent->_right==cur时，parent->_bf--

 后面会附上代码：