辗转相除法求最大公约数，进而求===＞最小公倍数

Posted 2021-09-20 再吃一个橘子

求最大公约数算法：

(1)辗转相除法

有两整数a和b：

① a%b得余数c

② 若c=0，则b即为两数的最大公约数

③ 若c≠0，则a=b，b=c，再回去执行①

例如求27和15的最大公约数过程为：

27÷15 余12          15÷12余3         12÷3余0           因此，3即为最大公约数

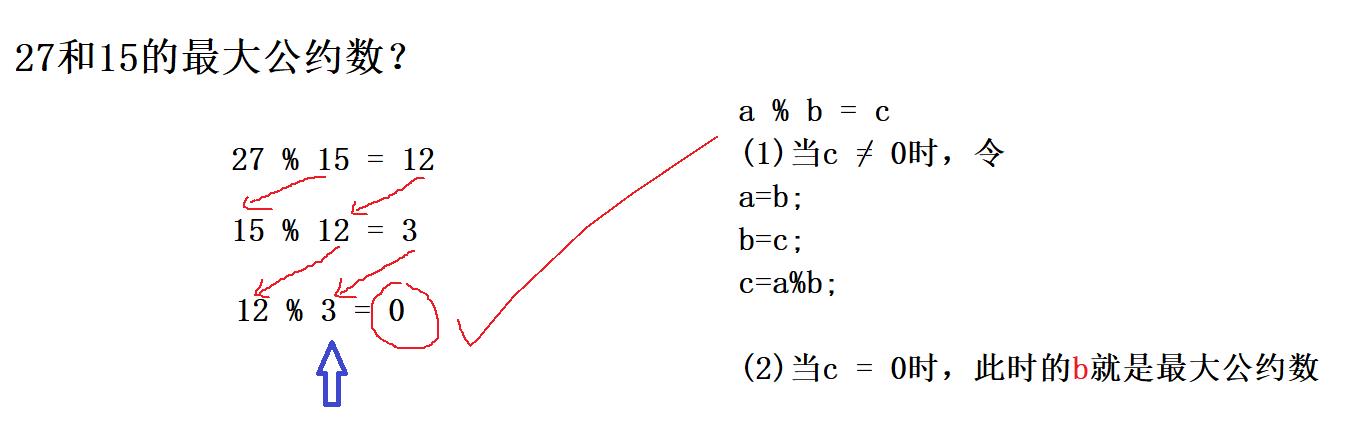
辗转相除算法：

int main()
{
	int a, b, c;
	scanf("%d %d", &a, &b);
	c = a % b;
	while (c != 0)
	{
		a = b;
		b = c;
		c = a % b;
	}
	printf("%d", b);

	return 0;
}

求最小公倍数算法：

最小公倍数 = 两整数的乘积 ÷ 最大公约数。

算法：

int main()
{
	int a, b, c;
	int max_yueshu, min_beishu;
	scanf("%d %d", &a, &b);
	//保留一下a,b的值
	int a1 = a;
	int b1 = b;
	c = a % b;
	while (c != 0)
	{
		a = b;
		b = c;
		c = a % b;
	}
	max_yueshu = b;
	min_beishu = (a1 * b1) / max_yueshu;
	printf("%d", min_beishu);

	return 0;
}