Leetcode-53.最大子序列和

Posted 2021-09-20 Booksort

• 分析问题
• 代码

题目链接

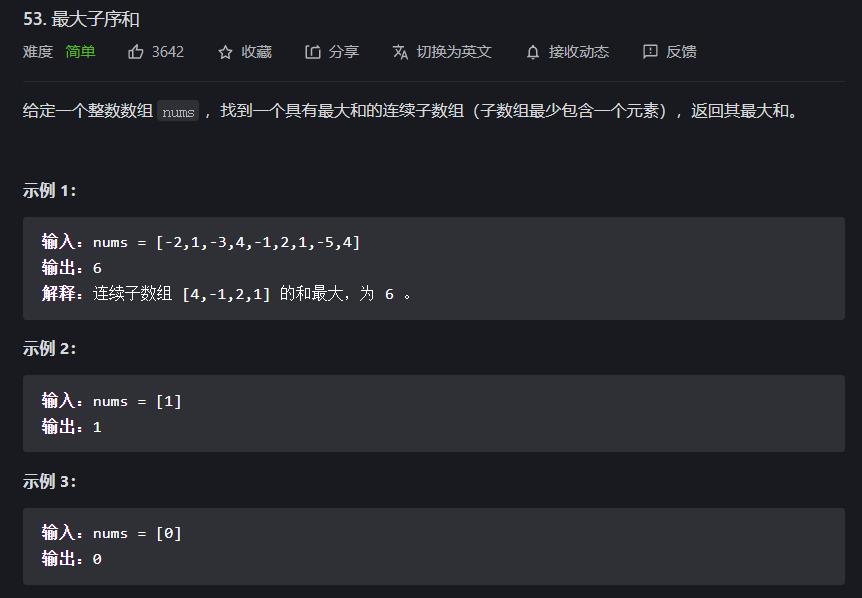
最近在学DP（动态规划），用动态规划的思路来解析这道题。动态规划作为一种设计方法后者说算法思想，可以考察这个问题的所有解，并最终得到最优解。
DP实现步骤

1. 定义状态
2. 状态转移（状态之间的递推关系）
3. 算法实现

对于使用DP算法的问题，需要寻找问题的关键，要将问题给抽象出来，并寻找最相似的子问题。

DP算法解决问题有三大特点

1. 把原有问题分解成几个相似的子问题
2. 所有的子问题只需要解决一次
3. 储存需要的子问题的解（用已得到最优的解）

使用场景：最大/小值、其条件是否可行、方案的个数。

分析问题

问题：数组中的最大连续和。

子问题：局部元素构成的数组，它的最大连续和

状态：F(i):前 i 个元素组成的数组，它的最大连续和。

转移方程：F(i):F(i-1)—求F(i)的数组中最大的连续和，就意味着要知道F(i-1)数组中的最大的连续和。但存在一个问题是，我们并不知道，F(i-1)的最大连续和是否有数组中[i-1]个元素，就是说

求F(4)的最大连续和，要知道F(3)的最大连续和。但是我们不知道，其最大连续和中元素a[3]是否也在其中。
由于，不确定最后一个元素是否也在其中，就无法建立相应的递推关系，转移方程也就无法确定。

那么这个状态就存在问题，需要寻找新的状态。

明确一下：我们刚刚的状态转移方程无法建立，是因为无法保证最后一个元素也一定参与在状态之间的递推关系中。所以我们可以着手考虑有什么方法让最后一个元素一定在状态转移中。

还有一个重要思路：线性DP有两种方法，顺推与逆推。

我们无法判断最后一个元素，那么就可以尝试从最后一个元素开始考虑。

如果我们保存每个以最后一个很元素结尾的子数组的最大连续和，然后统一比较，那么我们就能得到数组中最大连续和。

我刚开始对这个思路是比较迷惑的，因为我想这怎么得到最大连续和，如果最大连续和是数组中剑的一组连续元素怎么判断。

但是，DP之所以可以得到全局最优解，是因为DP可以利用其他状态的解。DP可以把之前子问题的计算结果记录为状态，然后把状态储存在状态表中，后面的子问题可以直接查状态表，这样既可以避免重复运算，也可以全局规划。

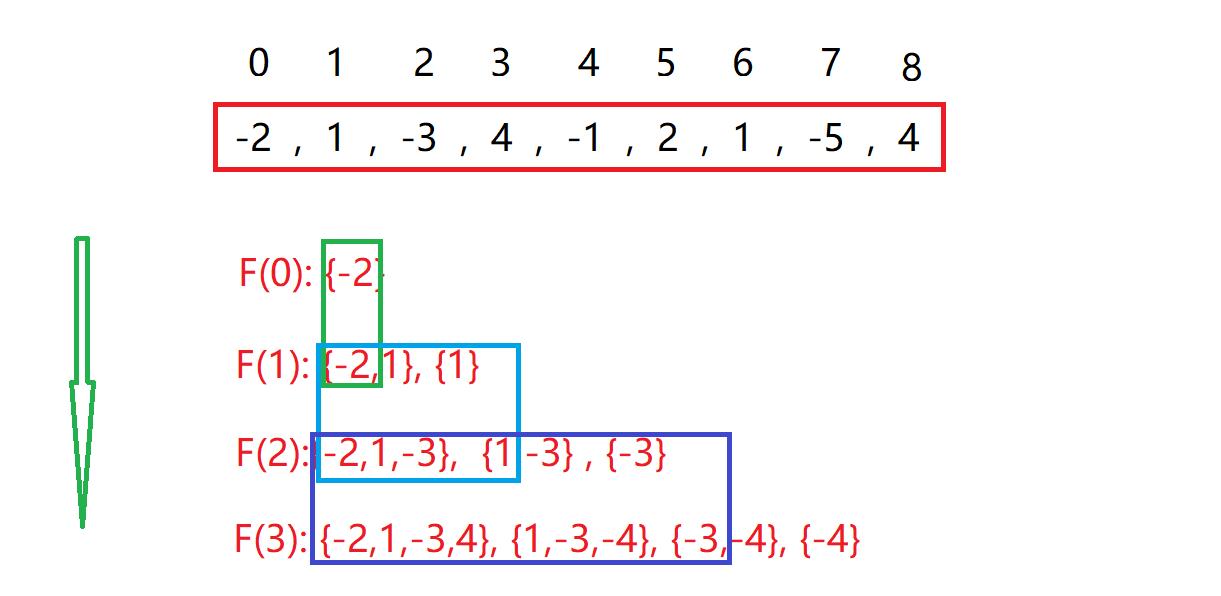
这些，看出来什么东西没？如果这么延申下去。可以得到所有以各个元素结尾的子数组的集合。如果要找连续的最大的和，只需要比较f(i-1)中的最大和与a[i]个元素相加之和与a[i]比较判断那个最大。

实际上，这个是列出f(i)的所有的子集，并保存子集的最大的和，而最后的sum(f(i))+a[i]也是为了比较所有的子集。而依靠递推关系，可以利用前面的解来求得最大值。

只要将所有以i结尾的数组的子集的最大和保存起来（符合保存要利用的子问题的解的算法要求）。

可能还是会有疑问，这个是怎么保证最终的一定是最大的子集。

我们保证的是，sum=max(sum+a[i],a[i]),这个sum+a[i]与a[i]就可以保证列举了所有的子集，sum就意味着前面子集的最大（根据状态之间的递推关系）。再储存在数组里，最后，数组里最大的元素就是整个数组的最大连续和。

代码

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int sum=0;
        int Max=nums[0];
        for(auto e:nums)
        {
            sum=max(sum+e,e);
            Max=sum>Max?sum:Max;
        }
        return Max;
    }
};

大概这题就这样，使用逆推的方式来以子集的最大值来表示最大数值。