1151 LCA in a Binary Tree

Posted 2021-09-20 CSU迦叶

目录

解法一思路

结果

解法一代码

---

解法一思路

1. 根据先序和中序建树

2. 对树进行深度优先遍历，找到每一个结点的父节点(注意：由于值的范围是int，直接用可能导致溢出，所以采用值在中序/先序中的下标来映射)

3. 对于读入的值，先判断有没有出现过，如果都出现过，分别得到两个结点的祖先序列(顺序是从自身到根节点)，然后进行双循环比对。最后将得到的结点分别和两个输入值比较来输出结果。

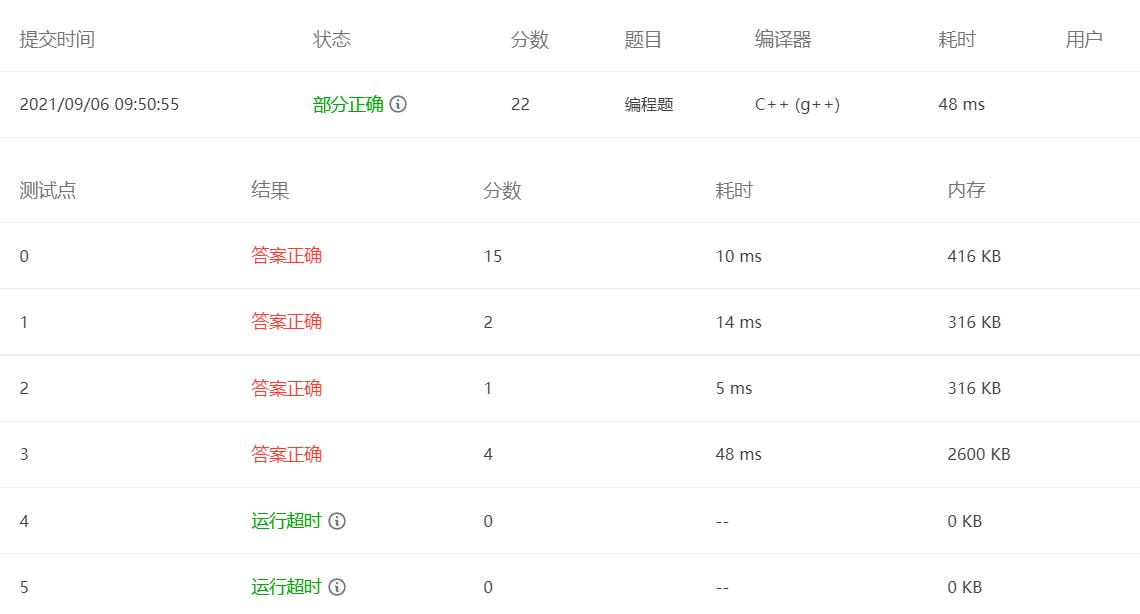
结果

最后两个用例超时

解法一代码

#include<cstdio>
#include<algorithm>
#include<cmath>
#include<iostream>
#include<queue>
#include<string>
#include<map>
#include<vector>
#include<set>

using namespace std;

const int maxn = 10001;
const int SUP = 2000000000;

int inSq[maxn],preSq[maxn];

//set<int> st;
map<int,int> appmp;

map<int,int> vToIdx;

int pre[maxn];//下标为inIdx 

vector<int> vi,vi1,vi2;

struct Node{
	int v;
	Node *lchild,*rchild;
}; 

void getAncest(int idx){
	
	while(pre[idx]!=idx){
		vi.push_back(inSq[idx]);
		idx = pre[idx];
	}
	
	return;
}

Node* create(int inL,int inR,int preL,int preR){
	if(preL>preR)return NULL;
	
	Node* root = new Node;
	
	root->v = preSq[preL];
	
	int k;
	for(k=inL;k<=inR;k++){
		if(inSq[k]==root->v)break;
	}
	
	int leftnum = k-inL;
	
	root->lchild = create(inL,k-1,preL+1,preL+leftnum);
	root->rchild = create(k+1,inR,preL+leftnum+1,preR);
	
	return root;
}

void DFS(Node* root){
	if(root==NULL)return;

	if(root->lchild!=NULL){
		int sonIdx = vToIdx[root->lchild->v];
		pre[sonIdx]= vToIdx[root->v];
		DFS(root->lchild);
	}
	if(root->rchild!=NULL){
		int sonIdx = vToIdx[root->rchild->v];
		pre[sonIdx]= vToIdx[root->v];
		DFS(root->rchild);
	}

	return;
}
 
int main(){
	
	int pair,n;
	cin>>pair>>n;
	
	for(int i=0;i<n;i++){
		cin>>inSq[i];
		appmp[inSq[i]] = 1;
		vToIdx[inSq[i]] = i;
	}
	for(int i=0;i<n;i++){
		cin>>preSq[i];
	}
	
	Node* root = create(0,n-1,0,n-1);
	
	int ridx = vToIdx[root->v];
	pre[ridx] = ridx;
	
	DFS(root);
	

	
	while(pair--){
		int v1,v2;
		cin>>v1>>v2;
		if(appmp[v1]==0){
			if(appmp[v2]==0){
				printf("ERROR: %d and %d are not found.\\n",v1,v2);
				continue;
			}else{
				printf("ERROR: %d is not found.\\n",v1);
				continue;
			}
		}else{
			if(appmp[v2]==0){
				printf("ERROR: %d is not found.\\n",v2);
				continue;
			}
		}
		
		
		vi.clear(); 
		getAncest(vToIdx[v1]);
		vi1 = vi;
		vi1.push_back(root->v);
		
		vi.clear();
		getAncest(vToIdx[v2]);
		vi2 = vi;
		vi2.push_back(root->v);	
		
		bool gotit = false;
		int LCA;
		
		for(int i=0;i<vi1.size()&&gotit==false;i++){
			for(int j=0;j<vi2.size();j++){
				if(vi1[i]==vi2[j]){
					LCA = vi1[i];
					gotit = true;
					break;
				}
			}
		}
		
		if(LCA==v1){
			printf("%d is an ancestor of %d.\\n",v1,v2);
		}else if(LCA==v2){
			printf("%d is an ancestor of %d.\\n",v2,v1);
		}else{
			printf("LCA of %d and %d is %d.\\n",v1,v2,LCA);
		}
	}

	return 0;
}