直接选择排序堆排序的联系与区别

Posted 2021-09-20 sanqima

    在数据结构中，直接选择排序、堆排序，都属于选择排序，即每次从待排序的序列中选出最小的关键字，把它放到已排序的末尾，直到整个序列变成有序为止。其时间复杂度、空间复杂度、稳定性的对比如下：

算法对比	直接选择排序	堆排序
平均时间复杂度	O(n^2)	O(nlogn)
最坏情况	O(n^2)	O(nlogn)
最好情况	O(n^2)	O(nlogn)
空间复杂度	O(1)	O(1)
属于稳定算法	不属于	不属于

1、直接选择排序

    基本思路：假设记录放在R[0,n-1]之中，R[0,i-1]是有序区，R[i,n-1]是无序区，且有序区所有关键字均小于无序区所有关键字。需要将R[i]添加到R[0,i-1]之中，使R[0,i]变成有序。每一趟排序，都会从无序区R[i,n-1]里选中一个最小的关键字R[k]，使其与R[i]进行交换，这样R[0,i]就变成有序的了，直到i=n-1为止。
//直接选择排序源码:

//直接选择排序2
vector<int> SelectionSort2(vector<int> &list) {
	int len = list.size();
	for (int i = 0; i < len - 1; i++) {
		int k = i;
		for (int j = i + 1; j < len; j++) {
			if (list[j] < list[k]) //用k记录无序区中最小元素的索引
				k = j;
		}

		int tmp = list[i];
		list[i] = list[k];
		list[k] = tmp;
	}

	return list;
}

2、堆排序

    堆是一颗顺序存储的完全二叉树，它分为2种：大根堆、小根堆。

• 若父节点比左右孩子都大，则为大根堆；
• 若父节点比左右孩子都小，则为小根堆；

    基本思路：首先，将R[1,n]调整为堆(这个过程称为初始建堆)，交换R[1]和R[n]；然后，将R[1,n-1]调整为堆，交换R[1]和R[n-1]；如此反复，直到交换了R[1]和R[2]为止。

    堆排序的第一步为：将一个元素序列调整为堆。在R[i+1,m]已经是堆的情况下，可按下述方法(也叫筛选法、调整法)，将R[i,m]调整为以R[i]为根的堆。

• 从R[2i]和R[2i+1]中选出关键字较大者，不妨假设R[2i]较大，再比较R[i]和R[2i]的关键字，若前者较大，则说明以R[i]为根的子树已经是堆，不必作任何调整；否则，则要交换R[i]和R[2i]。交换后，以R[2i+1]为根的子树仍是堆，而以R[2*i]为根的子树由于根节点关键字已经改变可能不再满足堆的定义，需要做调整。
• 重复上述过程，将以R[2*i]为根的子树调整为堆，如此一层一层进行下去，直到排到树叶位置为止。

//堆排序源码

/-------------------- 堆排序 ---------------
//调整堆
void heapAdjust(vector<int> &list, int parent, int length) {
	int tmp = list[parent];      //保存父节点
	int child = 2 * parent + 1;  //左孩子索引
	while (child < length)
	{
		//如果parent有右孩子，则要判断左孩子是否小于右孩子
		if (child + 1 < length && list[child] < list[child + 1])
			child++;

		//父节点大于子节点，就不用做交换
		if (tmp >= list[child])
			break;
		//将较大子节点的值赋值给父节点
		list[parent] = list[child];
		parent = child;

		//找到下一个左孩子
		child = 2 * parent + 1;
	}
	list[parent] = tmp;
}

//堆排序
void HeapSort(vector<int> &list) {
	int len = list.size();
	for (int i = len / 2 - 1; i >= 0;i--) {
		heapAdjust(list, i, len);
	}

	for (int i = len - 1; i > 0;i--)
	{
		int tmp = list[0];
		list[0] = list[i];
		list[i] = tmp;
		heapAdjust(list, 0, i);
	}
}

说明：完全二叉树，是一种有序树，因为它区分左子树和右子树。

• 定义：若一颗二叉树，最多只有最下两层的结点度数(分支数)可以小于2，并且最下面一层的叶子结点依次排列在该层的最左边的位置上，则该二叉树就称为完全二叉树。如图(1)所示。

图(1) 完全二叉树的图例

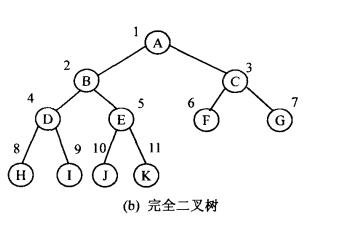
3、完整源码

//seletionsort.cpp

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

//直接选择排序1
vector<int> SelectionSort(vector<int> &list) {
	int len = list.size();
	for (int i = 0; i < len - 1;i++) {
		int tmpIndex = i;
		for (int j = i + 1; j < len; j++) {
			if (list[j] < list[tmpIndex])
				tmpIndex = j;
		}

		int tmpData = list[i];
		list[i] = list[tmpIndex];
		list[tmpIndex] = tmpData;
	}

	return list;
}

//直接选择排序2
vector<int> SelectionSort2(vector<int> &list) {
	int len = list.size();
	for (int i = 0; i < len - 1; i++) {
		int k = i;
		for (int j = i + 1; j < len; j++) {
			if (list[j] < list[k]) //用k记录无序区中最小元素的索引
				k = j;
		}

		int tmp = list[i];
		list[i] = list[k];
		list[k] = tmp;
	}

	return list;
}


//输出所有的元素
void printList(vector<int> list){
	for (int i = 0; i < list.size(); i++){
		printf("%d ", list[i]);
		if ((i + 1) % 5 == 0)
			printf("\\n");
	}
	printf("\\n");
}

//输出前K大的元素
void printListTopK(vector<int> list, int top) {
	if (top >list.size() || top <= 0){
		printf("the top is out of range!");
		return;
	}

	int cnt = 0;
	int nBase = list.size() - 1;
	for (int i = nBase; i > nBase - top; i--){
		printf("%d ", list[i]);
		cnt++;
		if ( cnt % 5 == 0)
			printf("\\n");
	}
	printf("\\n");
}


//-------------------- 堆排序 ---------------
//调整堆
void heapAdjust(vector<int> &list, int parent, int length) {
	int tmp = list[parent];      //保存父节点
	int child = 2 * parent + 1;  //左孩子索引
	while (child < length)
	{
		//如果parent有右孩子，则要判断左孩子是否小于右孩子
		if (child + 1 < length && list[child] < list[child + 1])
			child++;

		//父节点大于子节点，就不用做交换
		if (tmp >= list[child])
			break;
		//将较大子节点的值赋值给父节点
		list[parent] = list[child];
		parent = child;

		//找到下一个左孩子
		child = 2 * parent + 1;
	}
	list[parent] = tmp;
}

//堆排序
void HeapSort(vector<int> &list) {
	int len = list.size();
	for (int i = len / 2 - 1; i >= 0;i--) {
		heapAdjust(list, i, len);
	}

	for (int i = len - 1; i > 0;i--)
	{
		int tmp = list[0];
		list[0] = list[i];
		list[i] = tmp;
		heapAdjust(list, 0, i);
	}
}

//找出堆中前K大的元素
vector<int> HeapSortTopK(vector<int> &list, int top) {
	vector<int> topNode;
	int len = list.size();
	//进行len/2-1次调整
	for (int i = len / 2 - 1; i >= 0;i--) {
		heapAdjust(list, i, len);
	}

	//输出元素(求前K大)
	for (int i = len - 1; i >= len - top;i--)
	{
		//将堆顶与堆的第i个元素进行互换
		int tmp = list[0];
		list[0] = list[i];
		list[i] = tmp;

		//将最大值加入vector
		topNode.push_back(tmp);

		//重新构造堆
		heapAdjust(list, 0, i);
	}
	return topNode;
}

int main() {

	int arry[5] = { 20, 40, 50, 10, 60 };
	vector<int> dataVec(arry, arry + 5);

	//1)直接选择排序
	//SelectionSort(dataVec);
	//printList(dataVec);

	//2) 输出前K大的元素
	//HeapSortTopK(dataVec, 3);
	//printListTopK(dataVec, 3);

	//3）堆排序
	HeapSort(dataVec);
	printList(dataVec);

	system("pause");
	return 0;
}

4、参考文献

李春葆.数据结构习题与解析B级.2006