后缀数组（学习心得）

Posted 2021-09-20 zjj0624

后缀数组
后缀数组是一种处理字符串的利器，很多字符串的问题都可以通过后缀数组来实现。
后缀数组说简单一点就是对一个字符串的所有后缀子串进行排序。
我来举个例子，比如字符串banana
刚开始的时候它的后缀子串是
a
na
ana
nana
anana
banana
就是从主串的每个点i到结尾形成的这些子串。
后缀数组就是把这些子串按字典序来排个序。
a
ana
anana
banana
na
nana
具体的排序过程看起来非常痛苦，其实我们并不需要掌握是怎么排序的，我们只需要理解排序以后的数组就可以了，具体的排序就是直接套板子就可以了。
这个过程的时间复杂度是$(n\ast logn)$
我们学习算法肯定是来解决问题的，我们现在对这个字符串的后缀子串排序以后有什么用呢？
接下来就需要引出三个经常用到的数组（这三个数组具体求的过程也是直接套板子就可以，我们只需要知道这三个数组的作用，不需要知道是怎么求出来的）
$sa$数组的作用就是求排名为i的后缀子串是谁。
$rank$数组的作用就是求第i个后缀子串的排名是多少。
rank数组和sa数组是相互的。
$height$数组的作用就是求sa[i-1]的后缀和sa[i]的后缀的最长公共前缀。
我来举个例子,还是拿banana这个字符串来说。
我们已经对字符串排好序了。
比如我们要求$height[3]$
我们知道$sa[2]$的字符串是ana，$sa[3]$的字符串是anana,所以他们的最长公共前缀就是ana,所以$height[3]=3$
这样后缀数组就已经介绍完啦。
接下来就是板子，我们只需要知道怎么用就可以了，具体里面的过程其实我们在做题中不经常用到。

int x[N],y[N],c[N],rk[N],sa[N],h[N]; //x,y,c都是辅助函数
char s[N];//字符串
void get_sa(){
    for(int i = 1 ; i <= n ; ++i) c[x[i] = s[i]]++;
    for(int i = 2 ; i <= m ; ++i) c[i] += c[i - 1];
    for(int i = n ; i ; --i) sa[c[x[i]]--] = i;
    for(int k = 1 ; k <= n ; k <<= 1){
        int num = 0;
        for(int i = n - k + 1 ; i <= n ; ++i) y[++num] = i;
        for(int i = 1 ; i <= n ; ++i){
            if(sa[i] > k) y[++num] = sa[i] - k;
        } 
        for(int i = 1 ; i <= m ; ++i) c[i] = 0;
        for(int i = 1 ; i <= n ; ++i) c[x[i]]++;
        for(int i = 2 ; i <= m ; ++i) c[i] += c[i - 1];
        for(int i = n ; i ; --i) sa[c[x[y[i]]]--] = y[i],y[i] = 0;
        swap(x,y),num = 1;
        x[sa[1]] = 1; 
        for(int i = 2 ; i <= n ; ++i){
            x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] and y[sa[i] + k] == y[sa[i - 1] + k]) ? num : ++num;
        } 
        if(num == n) break;
        m = num;
    }
}
void get_h(){ 
    for(int i = 1 ; i <= n ; ++i) rk[sa[i]] = i;
    for(int i = 1,k = 0 ; i <= n ; ++i){
        if(rk[i] == 1) continue; 
        if(k) k--;
        int j = sa[rk[i] - 1];
        while(i + k <= n and j + k <= n and s[i + k] == s[j + k]) k++;
        h[rk[i]] = k;
    }
}

现在学习了板子，也了解了这三种数组，但是可能我们还是不了解后缀数组可以解决那些问题，接下来我们就来讲几类题型。
求最长重复子串（可重叠）
给你一个字符串，让你求这个字符串中最长重复子串。
我们来举个例子，就比如abcdabcda,最长的重复子串就是abcda.
解题思路
如果我们暴力的来解决这个问题
第一层需要枚举最长重复子串的长度，从n-1到1
第二层选择一个节点i进行枚举，比较的过程是是n，所以最终的时间复杂度应该是o(nnn)，如果用字符串hash的话，时间复杂度是o(n*n)的，时间复杂度还是有点高的。
接下来我们讲一下用后缀数组怎么来解决。
我们其实直接求出最大的$heigt[i]$就是答案了。
其实肯定有些人会有疑问，为什么最长重复子串是出现在排名相邻的后缀子串里面，我们知道排名越相近就说明两个字符串最长公共前缀就越大，所以最后最大的重复子串肯定出现在$height$里面，具体的大家可以好好思考一下。
求最长重复子串（不重叠）
问题:给你一个字符串,让你求出最长重复子串,并且没有重叠.
我们知道,如果我们还按刚才的思想,是没办法保证两个后缀是否中间有重复元素的,但是我们可以用$sa$数组来判断两个序列的最长公共前缀是否占有同一个元素呀.
我来举个例子.

解题思路
字符串是aabaaaab,下面的是排好序的后缀数组,我们来看
aab和aabaaaab,我们知道它们的最长公共子串是aab,是3,但是我们没法判断这个aab在主串中重叠了,这个时候我们就要用$sa$数组,它表示的是排名为i的后缀数组是哪一个字符串,我们知道aab是从i等于6开始的,aabaaaab是从1开始的,他们的差为6,大于了3,这就说明两个字符串之间是不重叠的.
这样我们就解决重叠的问题了,但是我们怎么判断最大呢?
我们可以二分答案,然后check函数就是判断是否有两个后缀之间的最长公共子串大于等于mid,且不重叠.
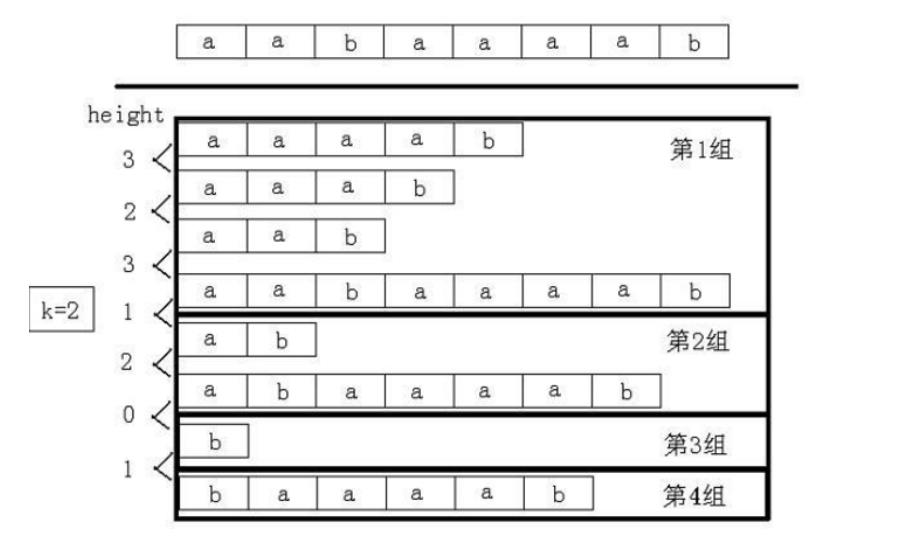
先二分答案，把题目变成判定性问题：判断是否存在两个长度为k的子串是相同的，且不重叠。把排序后的后缀分成若干组，其中每组的后缀之间的height值都不小于k。例如，字符串为“aabaaaab”，当k=2时，后缀分成了4组，如图所示。

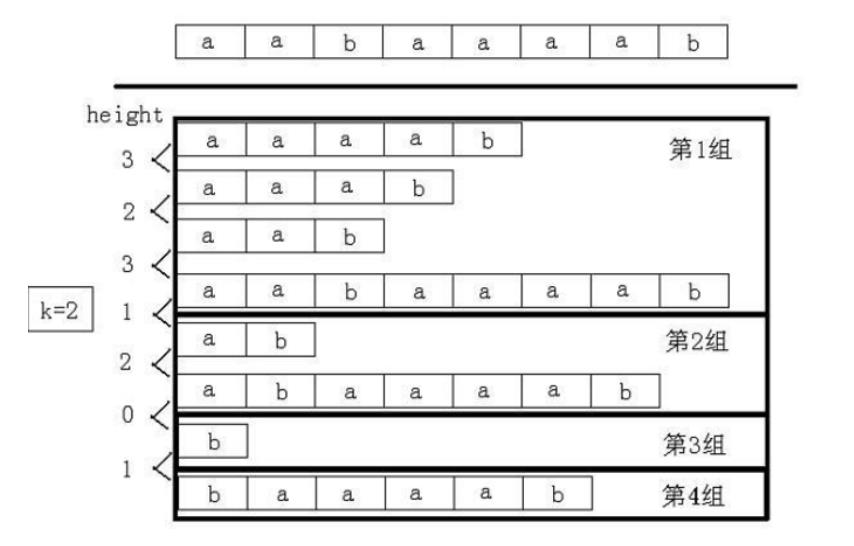
这样问题就解决了.
可重叠的k次最长重复子串
可重叠的,出现K次的最长重复子串.
比如k=4,字符串ababababa
出现4次,且最长的重复子串是aba.
解题思路
这个题也是二分答案,然后来判断是否可行,只不过这次的check函数不太一样,我们首先还是按照mid给后缀数组分成若干组,然后我们判断的是,同组中有没有等于或大于k的组,如果有就说明存在答案.
求字符串不同子串的个数
这个东西我们知道用trie树可以很容易的解决,只需要构建出trie树,树的节点数就是答案.
解题思路
但是这次我们用后缀数组来解决.
我们知道一个字符串的所有子串就是后缀数组的每一个前缀(这个一定要理解).
我们要去掉相同的,相同的肯定就是两个相邻前缀的最大公共子串,剩下的就是不同的了,如果有一个长度为n的字符串,它的子串数量是$n\ast (n-1)/2$
最后的答案就是
$n\ast (n-1)/2-$$\sum _{i=1}^{n}height[i]$