贪心算法_区间选点_区间分组_区间覆盖_huffman树

Posted 2021-09-20 一只特立独行的猫

文章目录

• • 区间问题
  • • 区间选点
    • • 原题链接：
      • 题目大意：
      • 思路：
      • 证明：
      • 代码：
    • 区间分组
    • • 原题链接：
      • 题目大意：
      • 思路：
      • 证明：
      • 代码：
    • 区间覆盖
    • • 原题链接：
      • 题目大意：
      • 思路：
    • 代码：
  • huffman树
  • • 合并果子
    • • 原题链接
      • 题目大意：
      • 思路：
      • 代码：

区间问题

区间选点

原题链接：

https://www.acwing.com/problem/content/907/

题目大意：

给定 N 个闭区间 [ai,bi]，请你在数轴上选择尽量少的点，使得每个区间内至少包含一个选出的点。
输出选择的点的最小数量。
位于区间端点上的点也算作区间内。

思路：

统计合并后不相交区间的个数。
1.对区间按右端点位置进行排序
2.如果一个区间的左端点在上一个大区间的右端点外面，则cnt++。

证明：

因为要统计的是不相交区间，所以采用按右区间排序较好理解。
当对一个区间按右端点排序后，以第一个区间为头，cnt记录的就是不相交区间的个数。必须保证每个不相交区间内有一个点，才能实现在每个区间至少有一个点。

代码：

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1e5+5;

struct Range{
    int l,r;
    bool operator< (const Range &w)const{
        return r<w.r;
    }
}range[N];

int n;

int main(){
    cin>>n;
    for(int i=0;i<n;i++){
        int a,b;
        cin>>a>>b;
        range[i]={a,b};
    }
    
    sort(range,range+n);//按右区间从小到大排序
    
    int ed = -2e9,cnt;
    for(int i = 0;i < n;i++){//统计不想交区间的个数
        if(range[i].l>ed){
            ed=range[i].r;
            cnt++;
        }
    }
    
    cout<<cnt<<endl;
    
    return 0;
}

区间分组

原题链接：

https://www.acwing.com/problem/content/908/

题目大意：

给定 N 个闭区间 [ai,bi]，请你将这些区间分成若干组，使得每组内部的区间两两之间（包括端点）没有交集，并使得组数尽可能小。
输出最小组数。

思路：

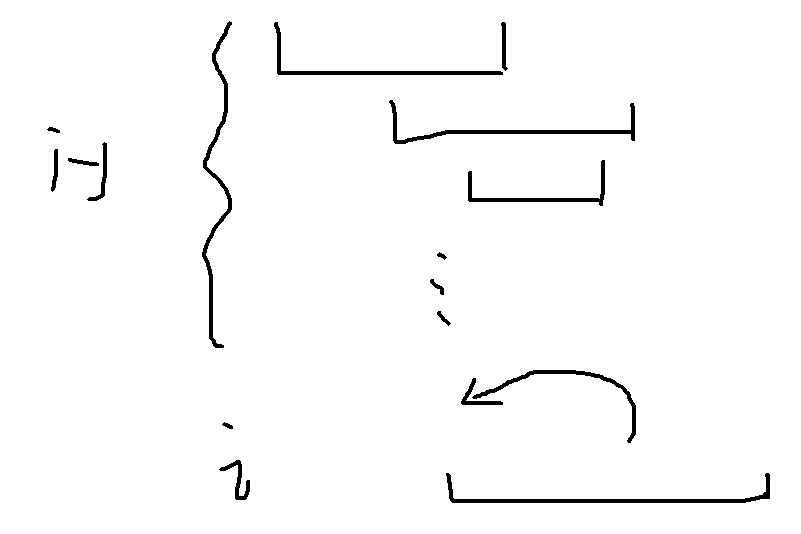
对左端点从小到大排序后，利用每一个堆存放已经有的集合的末尾，如果对于新区间v，在堆中存在一个区间k可以将v加入，则将v加入该区间，否则开辟一个新结点。

证明：

新区间的开头大于最小结尾的区间，则可以把这个区间加到后面。

新区间的开头小于等于最小结尾的区间，则将只能添加一个新的集合。

代码：

#include<iostream>
#include<algorithm>
#include<queue>
#include<vector>

using namespace std;

const int N = 1e5+5;

struct Range{
    int l,r;
    bool operator< (const Range &w)const{
        return l<w.l;
    }
}range[N];

int main(){
    int n;
    cin>>n;
    for(int i=0;i<n;i++){
        int a,b;
        cin>>a>>b;
        range[i] = {a,b};
    }
    
    sort(range,range+n);
    
    priority_queue<int ,vector<int >,greater<int > > q;//小根堆中存放区间的右端点
    for(int i=0;i<n;i++){
        auto v = range[i];
        if(q.empty()||v.l<=q.top()) q.push(v.r);//利用左端点进行判断
        else{
            q.pop();
            q.push(v.r);
        }
    }
    
    cout<<q.size()<<endl;
    return 0;
}

区间覆盖

原题链接：

https://www.acwing.com/problem/content/909/

题目大意：

给定 N 个闭区间 [ai,bi] 以及一个线段区间 [s,t]，请你选择尽量少的区间，将指定线段区间完全覆盖。输出最少区间数，如果无法完全覆盖则输出 −1。区间在-1e9-1e9之间，区间数量最多为100000个。

思路：

1.将所有区间按左端点从大大小排序。
2.从前往后依次枚举每个区间，在能覆盖start的所有区间中，找到一个右端点最远的区间。然后将start更新为这个右端点。

代码：

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1e5+5;

struct Range{
    int l,r;
    bool operator< (const Range &w)const{
        return l<w.l;
    }
}range[N];

int main(){
    int n,st,ed;
    cin>>st>>ed;
    cin>>n;
    for(int i=0;i<n;i++){
        int l,r;
        cin>>l>>r;
        range[i]={l,r};
    }
    
    sort(range,range+n);
    int res=0,success=false;
    for(int i=0;i<n;i++){
        int j=i,r=-2e9;
        while(j<n&&range[j].l<=st){
            //找右区间的最大值
            r=max(r,range[j].r);
            j++;
        }
        if(r<st){
            //出现断层
            res=-1;
            break;
        }
        res++;//选择的区间数+1
        if(r>=ed){
            //右端点到了区间的右边
            success=true;
            break;
        }
        st=r;
        i=j-1;
    }
    if(!success){
        res=-1;
    }
    cout<<res<<endl;
    return 0;
}

huffman树

合并果子

原题链接

https://www.acwing.com/problem/content/150/

题目大意：

n堆果子，每堆果子有自己的重量，每次合并任意两堆果子，合并的代价为两堆果子的重量和。需要把所有果子合并为一堆果子，求最小代价。

思路：

每次选取最小的两堆合并，然后将这新的一堆加入，以此类推，直到还有一堆果子，这就是最优解。

代码：

#include<iostream>
#include<queue>
using namespace std;

int main(){
    
    int n;
    priority_queue<int,vector<int>, greater<int > > q;//堆
    cin>>n;
    for(int i=0;i<n;i++){
        int x;
        cin>>x;
        q.push(x);
    }
    
    int res=0;
    
    while(q.size()>1){
        int a = q.top();q.pop();
        int b = q.top();q.pop();
        int c = a+b;
        res+=c;
        q.push(c);
    }
    
    cout<<res<<endl;
    return 0;
}