陈怡然团队最新研究：用复数神经网络提高梯度正则化准确度 | ICML 2021

Posted 2021-09-19 QbitAl

博雯 发自 凹非寺
量子位 报道 | 公众号 QbitAI

现在，我们可以用虚数来帮助AI算法抵御恶意攻击了！

这就是陈怡然团队提出的复数神经网络（CVNN），论文已被机器学习顶会ICML接收。

在对抗环境下，这种复数神经网络能够提高梯度正则化在实数输入的分类任务上的性能。

也就是说，不仅保证了鲁棒性，还能在性能上超越实数神经网络。

梯度正则化训练的复数网络

这是一种混合了实数和复数表达的多层复数网络。

想象一块巨石滚过崎岖的山谷，它的滚动路线会依据算法发生改变，最终目的就是落到最低点，也就是最佳答案附近。

为了避免巨石在一个错误的方向上直线下落，梯度正则化方法就倾向于选择“平缓路径”，使巨石缓慢下落。

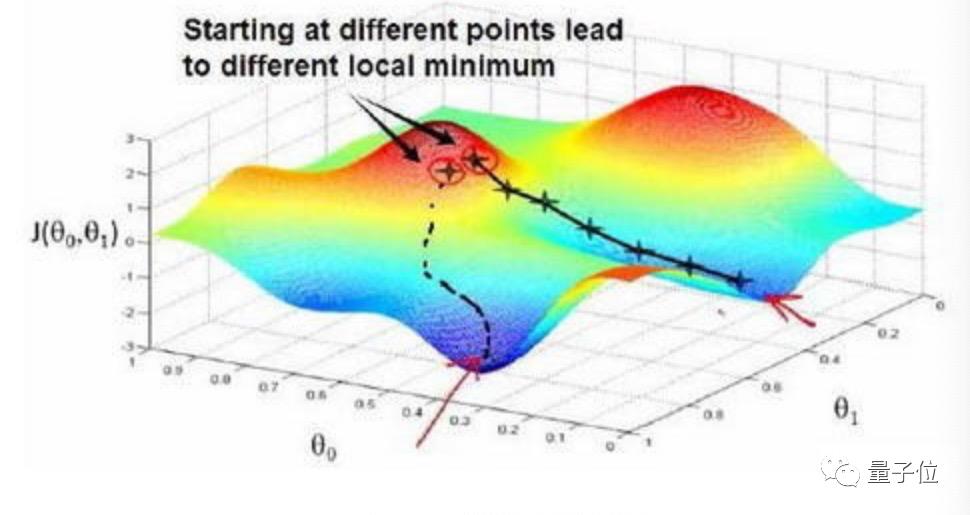
但这种“平缓路径”也会导致下落速度的减慢，也就是目标性能的下降。

而陈怡然团队提出的复数神经网络，则是一种能找到“梯形的”或更加“平坦”的视角的方法。

也就是说，当这种神经网络在一组图像上训练时，它能够使用带有虚部的复数调整网络内部参数，增加和累积变化，还允许波的相位进行放大或互相抵消。

因此，复数神经网络就能够有效防止这种由于正则化目标竞争而导致的目标性能下降。

我们也可以看到，定义一个有界的二维输入，两个或多个复数特征相加能够产生多个最大值和最小值：

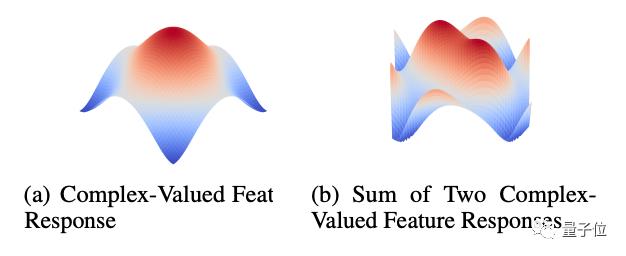
这就能够促进特征响应输入分布中自然变化的稳定性。

并且，对于复数神经网络的每个复数层，这一约束条件也分离了梯度规划范目标和标准：

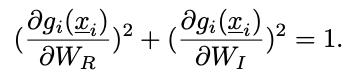
正是这种梯度约束，导致了复数网络在梯度正则化训练上展现出了比实数网络更好的效果。

复数网络性能更高，鲁棒性更强

陈怡然团队利用实验验证了复数网络的效果。

他们先将β设为一个控制正则化强度的超参数，同时让β取不同值。

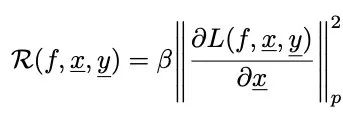
当β为0时，可以认为这是没有经历过梯度正则化，或对抗性训练的无防御性网络。

当β增加时，就如前文所分析的那样，这种无防御实数网络的性能会逐渐下降。

接下来，在MNIST、FashionMNIST等图像分类基准任务上对网络进行攻击，比较复数网络和实数网络在不同的β值（不同强度的梯度正则化训练）下的成果。

先在MNIST上对网络进行白盒攻击。

可以看到在β为0时，实数网络和复数网络都能在测试集上获得99%的准确性：

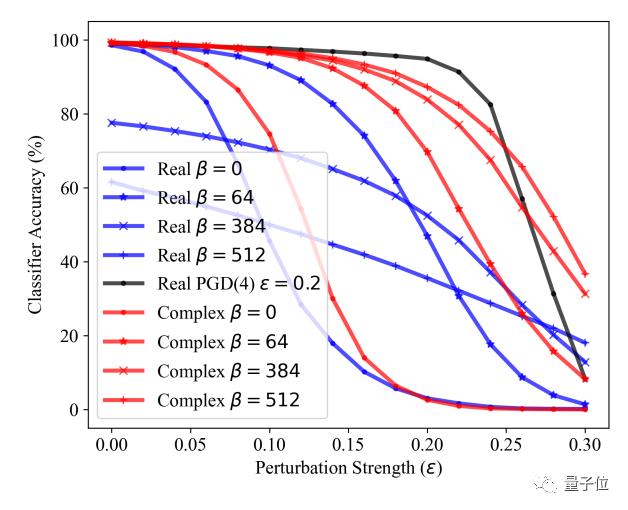
但当β值到512时，复数网络仍然能保证99%的准确度，而实数网络的准确度已经下降到了62%。

在FashionMNIST测试集上也一样。

随着β值的增加，网络的鲁棒性会增加。但在相同的准确度下，复数网络比实数网络在对抗样本上有更好的鲁棒性：

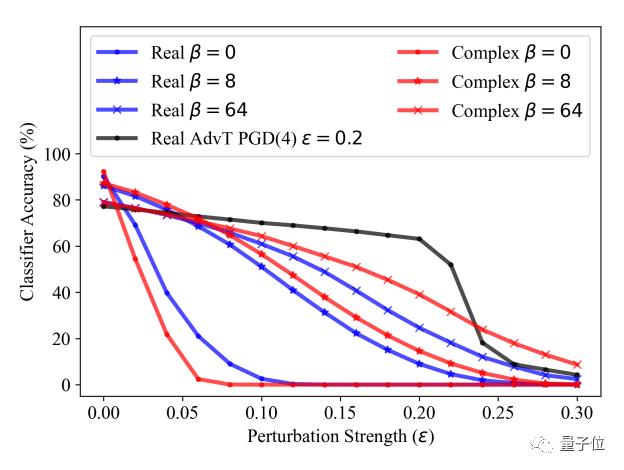
在SVHN和CIFAR-10数据集上进行训练的复数网络同样能在保留对抗准确性的同时，展现强大的鲁棒性。

而在基于迁移（transfer-based）的黑盒攻击中，其他网络也往往比复数网络更容易发生攻击的迁移，这表明它具有更好的抵抗力。

在基于访问（query-based）的黑盒攻击中，复数网络也在β值逐渐增加时，展现出了更高的准确率。

研究来自陈怡然团队

论文一作Eric Yeats为杜克大学电子与计算机工程专业的博士生，隶属于杜克计算进化智能中心（CEI）实验室。

论文二作陈怡然教授本硕均毕业于清华大学电子工程系，之后在普渡大学获得博士学位，现就任于杜克大学电子与计算机工程系。

陈怡然教授在2018年当选为IEEE Fellow，2021年成为ACM Fellow。

他主要专注于新型存储器及存储系统，机器学习与神经形态计算，以及移动计算系统等方面的研究。

三作李海为杜克大学电子与计算机工程专业的教授，主要研究方向为神经形态计算机系统，新兴内存技术等领域。

论文地址：
http://proceedings.mlr.press/v139/yeats21a.html

下载地址：
https://github.com/ericyeats/cvnn-security

参考链接：
https://www.eurekalert.org/news-releases/927064