(做题目学英语)PAT甲级第三题--1003 Emergency
Posted C_YCBX Py_YYDS
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了(做题目学英语)PAT甲级第三题--1003 Emergency相关的知识,希望对你有一定的参考价值。
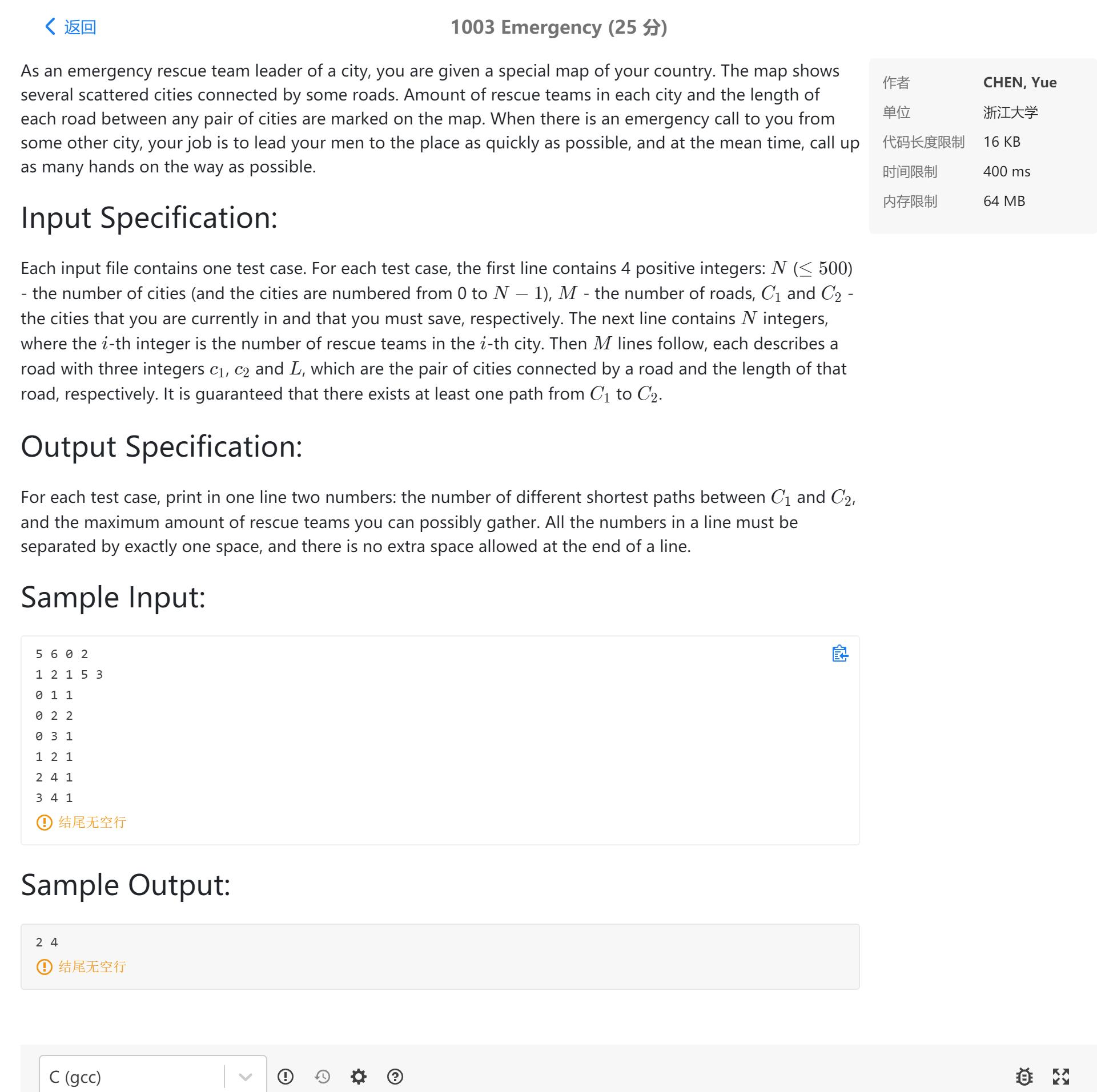
题目
卧槽,题目是真滴长,还是全英文,看个题目就要看半天。。
题目翻译
作为一个城市的紧急救援队队长,你会得到一张你所在国家的特殊地图。这张地图显示了几个被一些道路连接的分散的城市。每个城市的救援队伍数量和任何一对城市之间的每条道路的长度都被标记在地图上。当有一个紧急电话从其他城市给你,你的工作是尽快带领你的人到那个地方,同时,在路上召集尽可能多的人。
Input Specification:
每个输入文件包含一个测试用例。对每个测试案例:第一行包含四个正整数:N(城市的数量,并且每个城市被标记为0-N)、M(道路的数量、C1和C2(你目前所在的城市和你要去拯救的城市)。第二行包含N个整数第 i 个整数表示第 i 个城市的救援团队数量。紧接着跟上M行,每行用c1、c2、L来描述一条道路,表示c1和c2两个城市之间有一条长为L的道路。最后我们保证 C1 和 C2 至少存在一条路。
Output Specification:
对每个测试案例打印一行两个数字:C1 和 C2 之间的不同的最短路径数量 和 所能集结的最大救援团队数量。两个数字用空格隔开,并且末尾不存在任何空格。
单词积累
scatter(撒、散落)->scattered(分散的、离散的)
#例句:
#The map shows several scattered cities connected by some roads.
#这个地图显示了一些被道路连接的分散的城市。
#长难句分析:
# Amount of rescue teams in each city and the length of each road between any pair of cities are marked on the map.
# and将句子分为两部分,前一部分描述:每个城市的救援团队的数量,后一部分描述:每条道路的长度 ?什么样道路呢(对道路的描述)在任意一对城市中的道路 ?什么样的城市呢(对城市的描述)被标记在地图上的城市。
# 总的翻译为:每个城市救援队的数量,和在任意一对被标记在地图上的城市之间的道路长度。
call up 召集
#例句:call up as many hands on the way as possible.
#在路上召集尽可能多的帮手。
positive integers 正整数
题目解析
写这道题的时候把我烦死了!!!本来花了大概半个钟就写完了,结果不断debug,发现,原来是链式前向星的head数组的初始值有些不为-1(而有些又是-1,这就是迷了很久的原因),总结出的经验就是,任何情况不要随意的相信给数组直接初始化赋值会有用!最好自己进行初始化。。。 直接花了我一个小时去debug!!!还有个坑就是这是无向图,所以记得一组数据存两边。
- 通过前面的翻译可知题目是要我们求得 C1 到 C2 的所有最短路径的数量,以及这些最短路径中所能得到的最大救援团队的数量。
解决这个问题很简单,我们把它转为数学化的描述,实际上就是要我们求解,C1 到 C2 在路径边权和最小的情况下,路径点权和最大是多少,以及边权和最小的情况有多少个。
既然谈到单源最短路径,那么就不得不提一嘴Dijkstra算法,我之前有写过这样一篇博客Dijkstra算法详解。放在此题,我们只需多加两个数组记录数据,
nums[i]记录从 C1 到 i 的最短路径情况条数,w[i]表示从 C1 到 i 的点权和的最大值。
- 具体的实现:
- 当判定
dist[u] + e[u][v] < dist[v]的时候,不仅仅要更新dist[v],还要更新nums[v] = num[u], w[v] = weight[v] + w[u];。
从nums[C1]=1开始则后面到达的点都会继承前面的结果。
从w[C1]=weight[C1]开始则后面可达的点也都会去加上最新得到的紧急救援队。 - 如果
dist[u] + e[u][v] == dist[v],还要更新nums[v] += nums[u],而且判断一下是否权重w[v]更小,如果更小了就更新w[v] = weight[v] + w[u];。当出现相等情况时,说明可能得到了一条新的最短路径,这个时候就需要+=nums[u]来更新到达v的最短路径的数量。同时这个出现的新的路径可能比旧的路径上的点权和要大,所以我们也要判断更新w[v]。
总的来说:情况1可以看作是一条最短路径的更新情况,情况2则看作是 出现了多条最短路径时的更新情况。
链式前向星模板
然而我这次,想整点不一样的存图方式,然后就用了链式前向星。然后就不断Debug,但是我觉得吧,也算是增加了对链式前向星的熟练度了。
链式前向星理解了后,是真滴好写,但要注意这个边的数量控制,边的数量一般很大,所以注意edge数组开大一点。
用到的基本变量
int head[N]; //用于存入以该结点为起点的所有边的首个边的编号,没有任何边一般初始化为-1
int tot = 0; //表示已经存了多少个边,同时也兼任对下一片存储空间的定位。
struct Edge{
int to; //表示这是到哪个点的边
int len;//表示边的长度
int next;//类似静态链表,表示下一个边的序号
}edge[MaxN];
add()函数
也就相当于头插法
void add(int a,int b,int len){
edge[tot].to = b;
edge[tot].len = len;
edge[tot].next = head[a];
head[a] = tot;
tot++;
}
遍历方式
for(int i=head[node];i!=-1;i=edge[i].next){
...
}
解题代码
效率还行(写代码时把模块分成多个函数的好处在于有利于debug)
#include<bits/stdc++.h>
using namespace std;
#define MaxN 505
const int INF = 0x3f3f3f3f;
int N,M,C1,C2;
//用于存储有多少个最短路径 以及到达该点的最短路径中最多能集结多少个救援团队
int nums[MaxN];
int weight[MaxN];
int w[MaxN];
//Dijkstra需要的两个数组,一个存储是否完成最短路,一个存储最短路
bool visit[MaxN];
int dist[MaxN];
//链式前向星建图模块
int head[MaxN];
int tot = 0;
struct Edge{
int len;
int to;
int next;
}edge[550*550];
void add(int a,int b,int len){
edge[tot].to = b;
edge[tot].len = len;
edge[tot].next = head[a];
head[a] = tot;
tot++;
}
//输入数据接收模块
void Input(){
//注意这里一定要初始化为-1
memset(head,0xff,sizeof(head));
scanf("%d%d%d%d",&N,&M,&C1,&C2);
for(int i=0;i<N;i++){
scanf("%d",&weight[i]);
}
for(int i=0;i<M;i++){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
add(b,a,c);
}
}
//Dijkstra算法的模块
int findMin(){
int minV = C1;
int minDist = INF;
for(int i=0;i<N;i++){
if(visit[i])continue;
if(minDist>dist[i]){
minDist = dist[i];
minV = i;
}
}
visit[minV] = true;
return minV;
}
void Dijkstra(){
for(int k=0;k<N;k++){
int node = findMin();
if(node==C1)
break;
for(int i=head[node];i!=-1;i=edge[i].next){
if(!visit[edge[i].to]){
if(dist[edge[i].to]>dist[node]+edge[i].len){
dist[edge[i].to] = dist[node]+edge[i].len;
nums[edge[i].to] = nums[node];
w[edge[i].to] = weight[edge[i].to] + w[node];
}//如果有不同路径更新到这个最短距离,那么需要将nums和w进行更新,
//由于nums[i]表示出发点到i的最短路径条数,所以需要+=,而w[i]表示最短路径中的最大救援团队值。
//其实这个nums[i]的+=求得的只是到达i的路径条数,主要能变成到达i的最短路径条数,多亏了上面的的更新不断重置。
else if(dist[edge[i].to]==dist[node]+edge[i].len){
nums[edge[i].to] += nums[node];
w[edge[i].to] = max(w[edge[i].to],weight[edge[i].to] + w[node]);
}
}
}
}
}
//主函数模块
int main(){
Input();
//第一次的起点更新
memset(dist,0x3f,sizeof(int)*N);
dist[C1] = 0;
visit[C1] = true;
nums[C1] = 1;
w[C1] = weight[C1];
for(int i=head[C1];i!=-1;i=edge[i].next){
if(dist[edge[i].to]>dist[C1]+edge[i].len){
dist[edge[i].to] = dist[C1]+edge[i].len;
nums[edge[i].to] = nums[C1];
w[edge[i].to] = weight[edge[i].to] + w[C1];
}
}
//直接Dijkstra算法得出答案
Dijkstra();
//输出答案
printf("%d %d",nums[C2],w[C2]);
return 0;
}
以上是关于(做题目学英语)PAT甲级第三题--1003 Emergency的主要内容,如果未能解决你的问题,请参考以下文章
(学英语学算法)PAT甲级--All Roads Lead to Rome