时间序列预测的七种方法-python复现

Posted 2021-09-19 iuk11

前提：数据集为JetRail高铁的乘客数量，网上搜一下可以找到。数据集共18288行有效数据，第一列对应 ID ；第二列为Datatime，格式为日-月-年+时间，时间间隔为一小时；第三列为Count，表示该时段内乘客数量。

目录

• • • • 测试数据是否正确读入
      • 数据可视化
      • （一）朴素法
      • （二）简单平均法
      • （三）移动平均法
      • （四）简单指数平滑法(SES)
      • （五）霍尔特(Holt)线性趋势法
      • （六）Holt-Winters季节性预测模型
      • （七）自回归移动平均模型（ARIMA）
      • 总结

测试数据是否正确读入

import pandas as pd #pands别名pd
df = pd.read_csv('train.csv') #读取csv文件
print(df.head(5)) #读取前5行数据

数据可视化

$x$轴表示时间，$y$轴表示乘客数量。

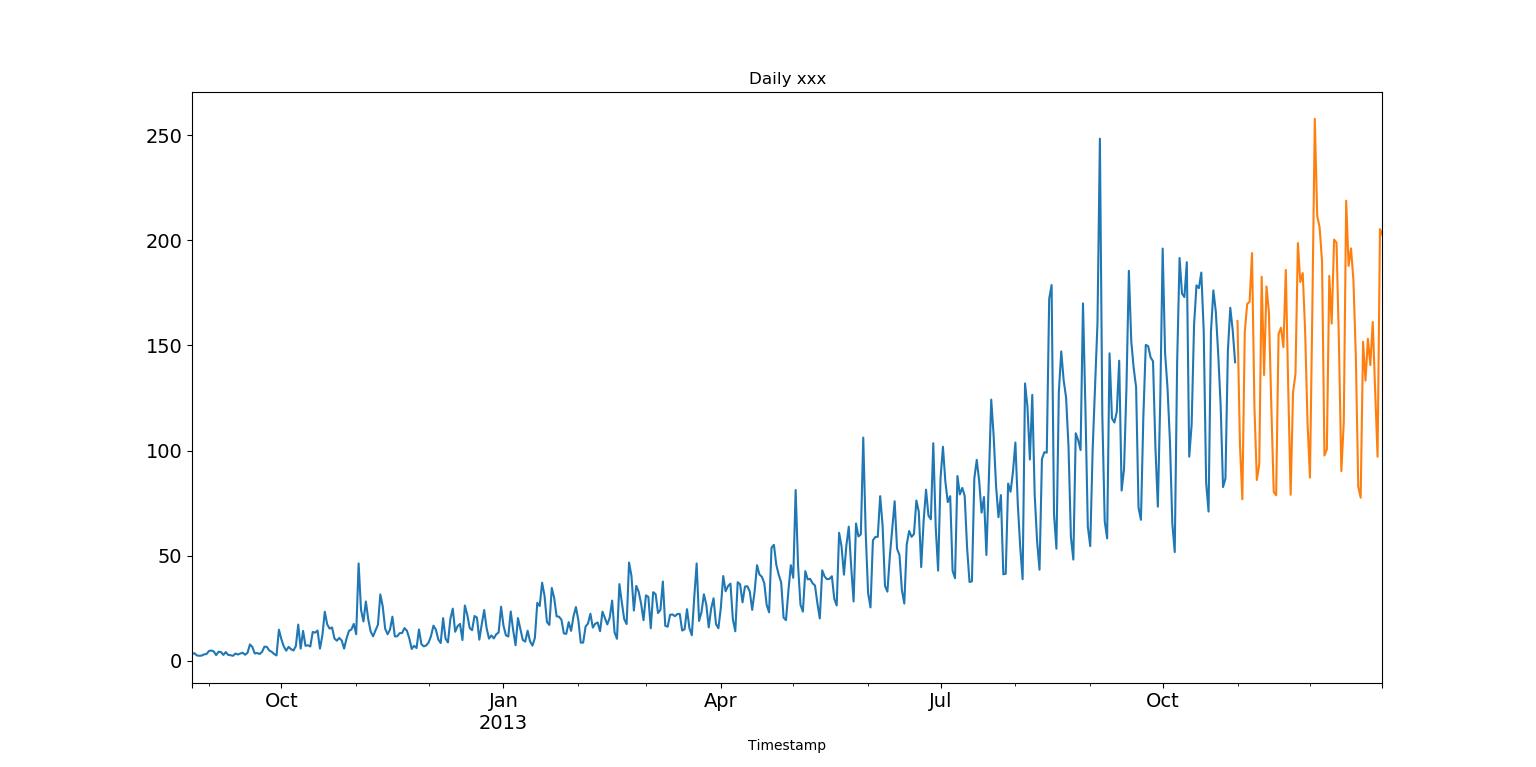
将数据拆分成两部分，[1,14]作为训练集，[15,16]作为测试集，测试集将与预测集进行均方根误差计算，检查预测的准确率。误差值越小，说明预测越准确。

df['Timestamp']=pd.to_datetime(df['Datetime'],format="%d-%m-%Y %H:%M")
代码解释：
arg–df['Datetime'],表示要转换为日期时间的对象
format，str，改变格式，解析时间的strftime
其它参数未用到，想了解可以查看pd.to_datetime()官方文档

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

df=pd.read_csv('train.csv',nrows=11856)
train=df[0:10392]#训练集
test=df[10392:]#测试集
df['Timestamp']=pd.to_datetime(df['Datetime'],format="%d-%m-%Y %H:%M")
df.index=df['Timestamp']  #在train文档中新增加一列Timestamp
df=df.resample('D').mean() #按天采样，计算均值

train['Timestamp']=pd.to_datetime(train['Datetime'],format="%d-%m-%Y %H:%M")
train.index=train['Timestamp']
train=train.resample('D').mean()

test['Timestamp']=pd.to_datetime(test['Datetime'],format="%d-%m-%Y %H:%M")
test.index=test['Timestamp']
test=test.resample('D').mean()

#数据可视化
train.Count.plot(figsize=(15,7),title='Daily xxx',fontsize=14)
test.Count.plot(figsize=(15,7),title='Daily xxx',fontsize=14)
plt.show()

（一）朴素法

应用情境：稳定性高的数据集。
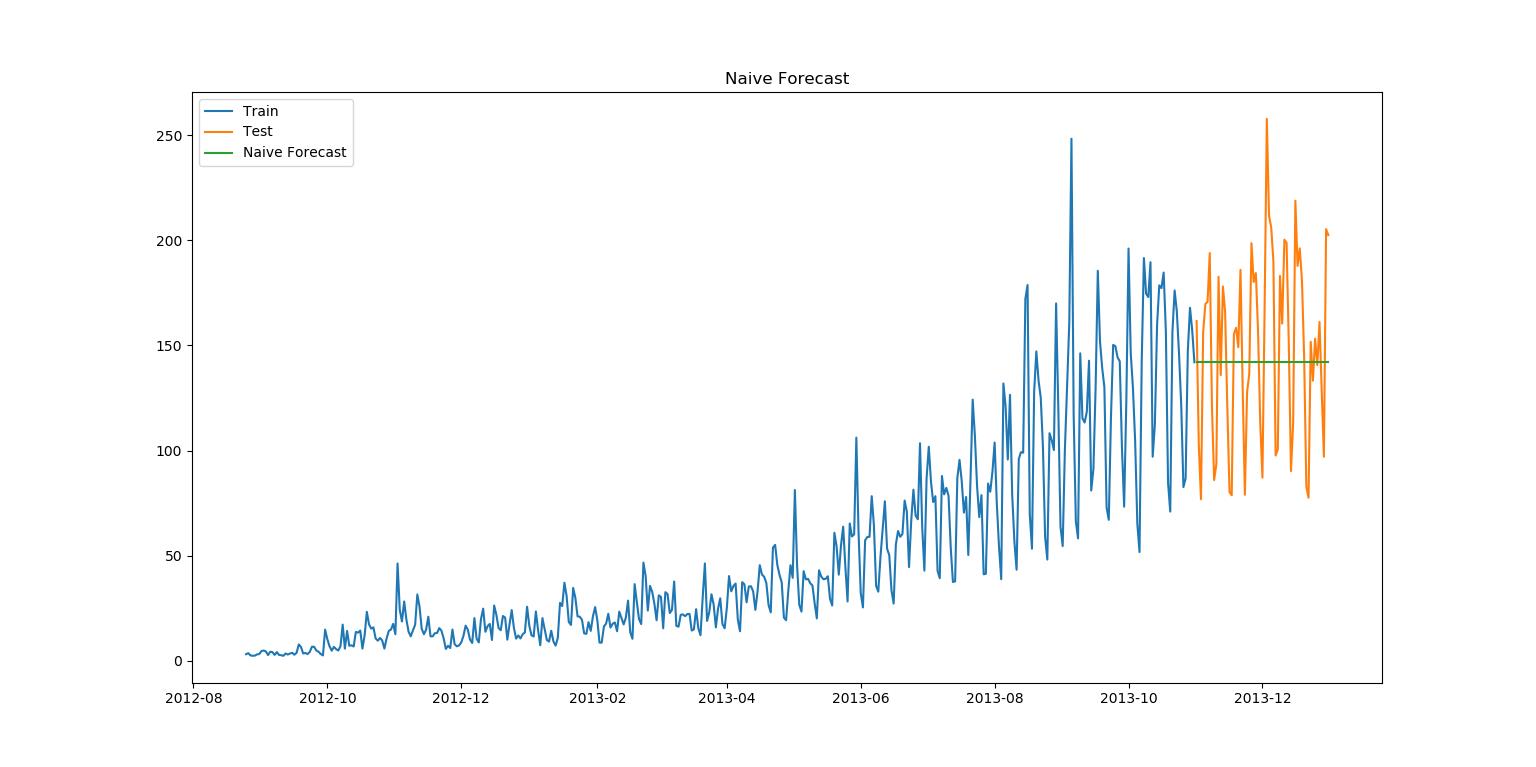
应用方法：以最后一个训练点为预测值的一条水平直线。
该数据集的均方根误差RMS为43.91640614391676。

plt.plot()函数说明
plt.plot(x, y, 'bs', label='xxx')
横轴为$x$轴，纵轴为$y$轴。$bs$表示蓝色方块点。$label$表示标题。

公式为：$$\widehat{y_{t+1}}=y_t$$
该代码需要连接上方数据预处理(拆分,改变格式)代码才能正常运行。

import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error
from math import sqrt
#
dd=np.asarray(train['Count']) #将train中的Count列转化为array(数组)形式
y_hat=test.copy()
y_hat['naive']=dd[len(dd)-1] #预测数据均为test的最后一个数值
plt.figure(figsize=(12,8))
plt.plot(train.index,train['Count'],label='Train')
plt.plot(test.index,test['Count'],label='Test')
plt.plot(y_hat.index,y_hat['naive'],label='Naive Forecast')
plt.legend(loc='best')
plt.title("Naive Forecast")
plt.show()
#均方根误差计算
rms = sqrt(mean_squared_error(test['Count'], y_hat['naive']))
print(rms)

（二）简单平均法

应用情境：每个时间段内的平均值基本保持不变的数据集。
应用方法：预测的价格和过去天(已知数据的)平均值的价格一致。
该数据集的均方根误差RMS为109.88526527082863。

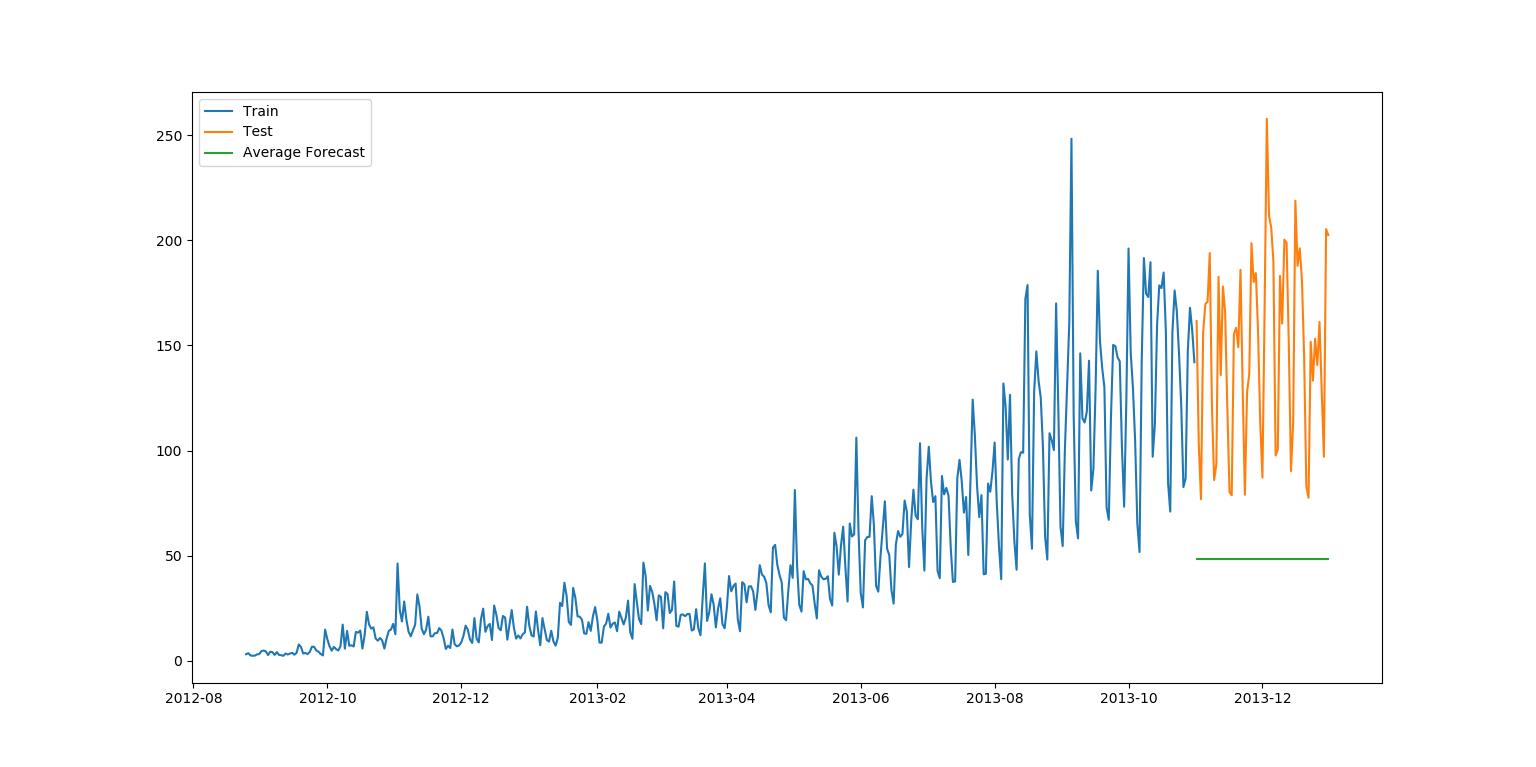
公式为：$${\hat{y}}_{x+1}=\frac{1}{x}\sum _{i=1}^x{y}_i$$
该代码需要连接上方数据预处理(拆分,改变格式)代码才能正常运行。

y_hat_avg=test.copy()
y_hat_avg['avg_forecast']=train['Count'].mean() #取train中Count列的平均值
plt.figure(figsize=(12,8))
plt.plot(train['Count'],label='Train')
plt.plot(test['Count'],label='Test')
plt.plot(y_hat_avg['avg_forecast'],label='Average Forecast')
plt.legend(loc='best') #对性能图做出一些补充说明的问题
plt.show()

rms = sqrt(mean_squared_error(test['Count'], y_hat_avg['avg_forecast']))
print(rms)

（三）移动平均法

应用情境：最后一个时间段内的平均值基本保持不变(平稳)的数据集。
应用方法：预测的价格和最近时期的平均值的价格一致。
该数据集的均方根误差RMS为46.72840725106963。

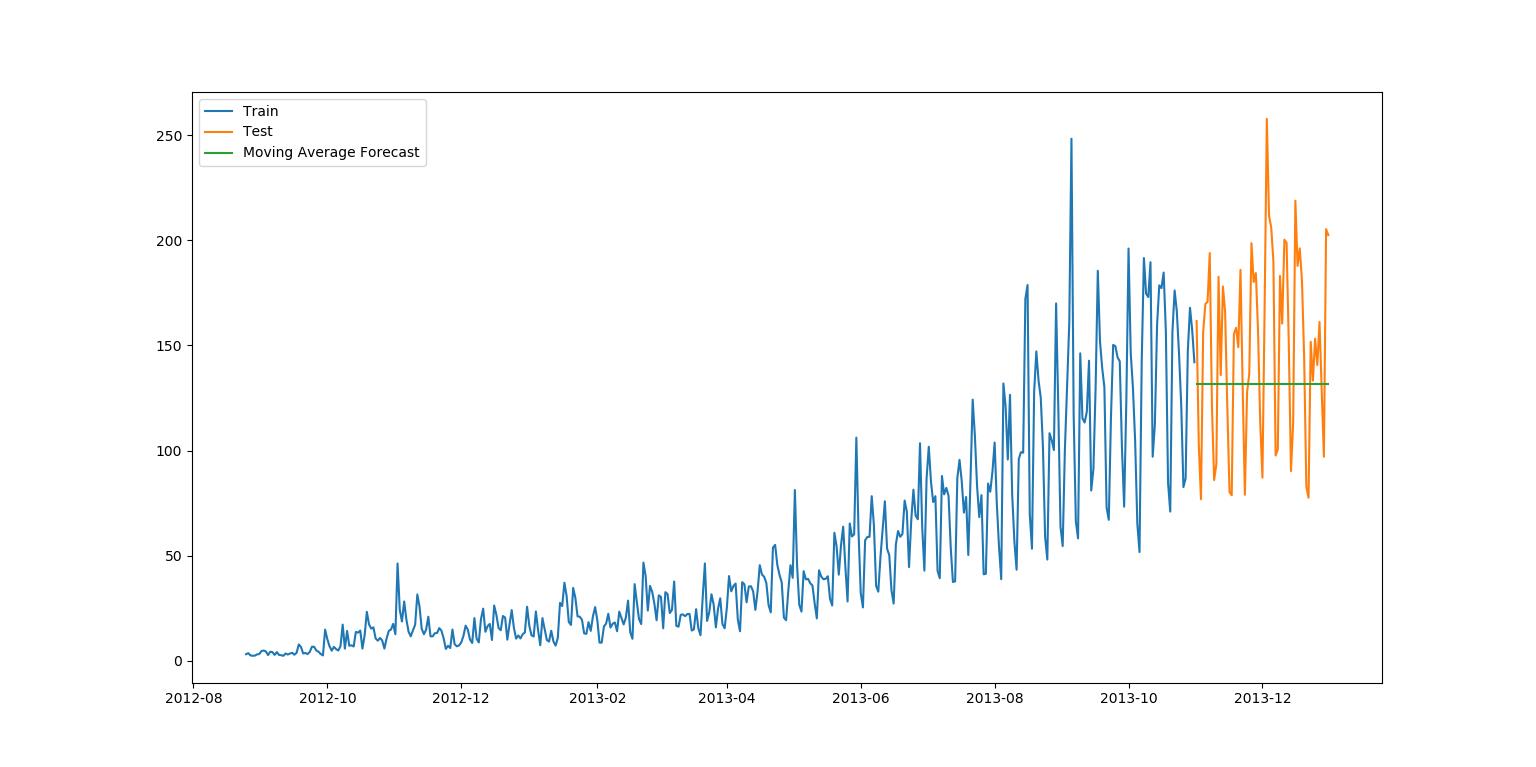
因为取最近时期的平均值，我们必须知道最近的时期是多少天(多长)，引入滑动窗口的概念，我们规定最近时期长度为 $p$ ，对于所有的 $i>p$：$${\hat{y}}_l=\frac{1}{p}(y_{i-1}+y_{i-2}+y_{i-3}+\dots +y_{i-p})$$
图示滑动窗口概念理解：

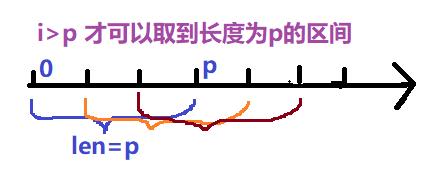
该代码需要连接上方数据预处理(拆分,改变格式)代码才能正常运行。

y_hat_avg = test.copy()
y_hat_avg['moving_avg_forecast']=train['Count'].rolling(60).mean().iloc[-1] #以p=60计算滚动平均值
plt.figure(figsize=(16,8))
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['moving_avg_forecast'], label='Moving Average Forecast')
plt.legend(loc='best')
plt.show()

rms = sqrt(mean_squared_error(test['Count'], y_hat_avg['moving_avg_forecast']))
print(rms)

（四）简单指数平滑法(SES)

应用情境：没有明显趋势或季节规律的预测数据。简单平均法和加权移动平均法的折中方法。
应用方法：预测的价值为每个时间段乘以该时间段的权重和，越接近当下(预测)的时间段赋予的权重越大。
该数据集的均方根误差RMS为43.357625225228155，α=0.6。(最终均方根误差可根据α的调节而降低)

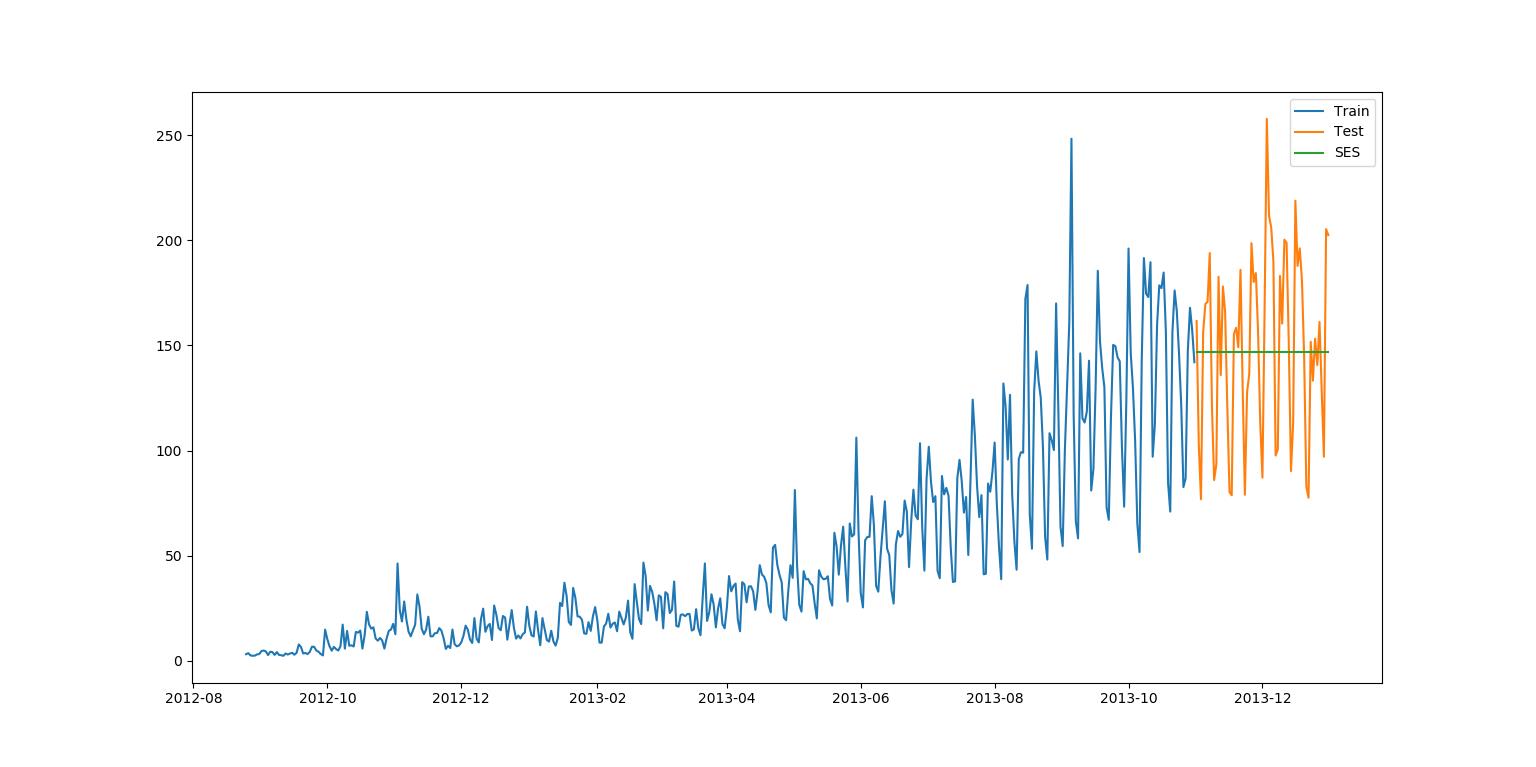
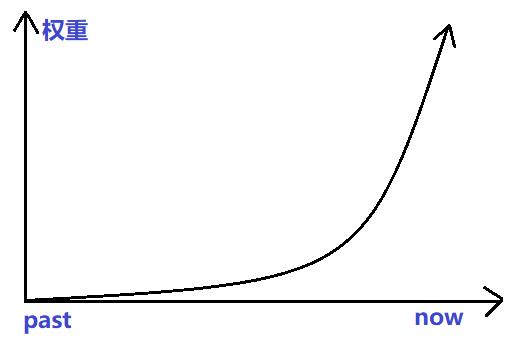
权重的赋予方式：从早到晚的每个时间段值的权重参数呈指数级下降。$${\hat{y}}_{T+1|T}=\alpha y_T+\alpha (1-\alpha )y_{T-1}+\alpha (1-\alpha {)}^2{y}_{T-2}+\dots$$其中 0≤α≤1 为平滑参数；$y_{T+1}$是$y_1$~$y_t$的值的加权平均值；预测值${\hat{y}}_x$为$\alpha \cdot y_t$与$(1-\alpha )\cdot {\hat{y}}_x$的和。即上述公式也可以写成： y ^ t + 1 ∣ t = α y t + ( 1 − α ) y ^ t − 1 ∣ t \\hat{y}_{t+1|t}=\\alpha y_t+(1-\\alpha)\\hat{y}_{t-1|t} y^​t+1∣t​=αyPython 炫技操作：合并字典的七种方法

90%人不知道的Python炫技操作：合并字典的七种方法

python 添加字符串的七种方法

Python 炫技操作：合并字典的七种方法

Python 炫技操作：条件语句的七种写法

Python 炫技操作：条件语句的七种写法