论文阅读|《基于拍卖的运输能力约束的单元零件调度协作机制》

Posted 2021-09-19 码丽莲梦露

《Auction-based cooperation mechanism for cell part scheduling with transportation capacity constraint》

International Journal of Production Research/2018

1 摘要

        本文研究了具有运输能力约束的单元零件调度问题。在该问题中，零件可能需要访问不同的单元，它们必须通过自动引导车辆(AGV)转移。目标是最小化整个过程的制造跨度。建立了一个整数非线性规划(INLP)模型，用于机器、agv的分配和各部件的调度。提出了一种合理的运输方式，并提出了一种基于拍卖的启发式方法来解决这一问题，重点解决了在加工和运输过程中机器与agv之间的协作问题。拍卖包括两个方面:AGV拍卖和机器拍卖。在这两种拍卖中，agv和机器分别充当拍卖人，零部件充当投标人。提出了一种改进的析取图模型，用于优化基于拍卖方法得到的可行解。通过数值实验对基于拍卖的方法和改进的析取图模型进行了验证。结果表明了基于拍卖的方法和改进的分离图模型的有效性，并表明了AGV能力对调度部件的影响。

2 介绍

        单元制造（CM）是一种生产系统，在该生产系统中，同类生产过程的部件被分组在不同的制造单元中进行生产。CM十分适用于高度定制和复杂产品的中小批量生产。

        根据单元数，CMS的研究可分为：

                （1）单单元部件调度（single-cell part scheduling,S-CPS）:运输主要在细胞（cell）内将进行，称为细胞内移动.

                （2）多单元部件调度（multi-cell part scheduling,M-CPS）:在M-CPS中，一个部件不能再一个细胞中完成所有加工，部件访问不同的细胞是不可避免的，相对于细胞内运动，细胞间运动更为重要，称为细胞间运动。

        这篇文章解决问题的环境为M-CPS，所有细胞中AGV相同。这篇文章需要解决的问题是：如何时为指定的AGV转移零件、直接移动到该零件或在AGV上完成现有零件的转移后;如果有两个或多个部件等待同一AGV加载，则AGV首先移动到哪个部件;如何确定在AGV上卸现有零件的顺序。

3 论文解读

3.1 问题描述

        本文提出了一个由多个制造单元组成的元胞制造系统。每个单元的机器、AGV和零件的分配是事先确定的。对于所有细胞，每种类型只有一台机器。每个部件都有特定的加工路线，每个操作都在一台机器上进行。当一个部件需要从一个单元移动到另一个单元时，需要通过AGV进行转移。我们假设每个部件的体积相同，AGV的容量为n，即每个AGV最多可以同时处理n个部件。我们把每个部件的装卸当作一项运输任务。不同细胞间的运输时间与细胞和工件有关。忽略细胞内运输时间。各细胞内AGV相同，尽量在不同细胞内内平均分配，在细胞间运输时，如果剩余空间足够大，可以将零件装载在AGV上。当零件在机器上完成最后一次加工后，可以立即离开制造系统进行处理。提出的问题的目标是得到一个最小完工时间的调度方案。

3.2 算法求解

3.2.1 生成初始解

        在具有运输能力约束的M-CPS问题中，由于供给与需求的关系在不同的时间点是可变的，拍卖商可以估计出机器和agv在每个时间点的资源价格，资源的价格可以揭示竞标者对资源的需求，引导拍卖商将资源分配给最渴望的人，既能使利润最大化，又能提高资源的利用率。因此，拍卖理论可以有效地解决运输能力约束下的M-CPS问题。机器与AGV的拍卖模型的主要结构如下：

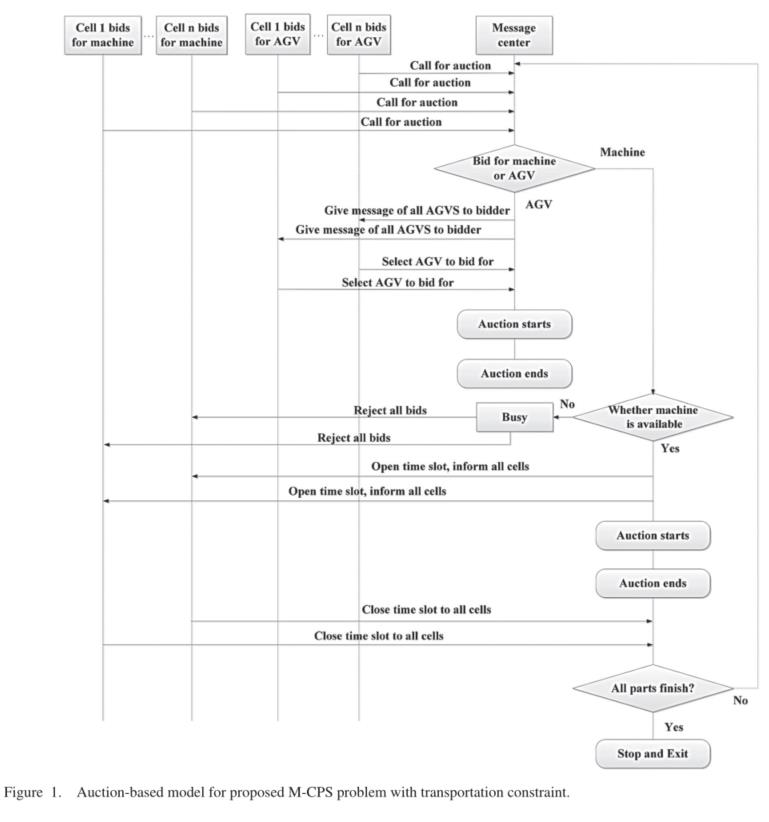
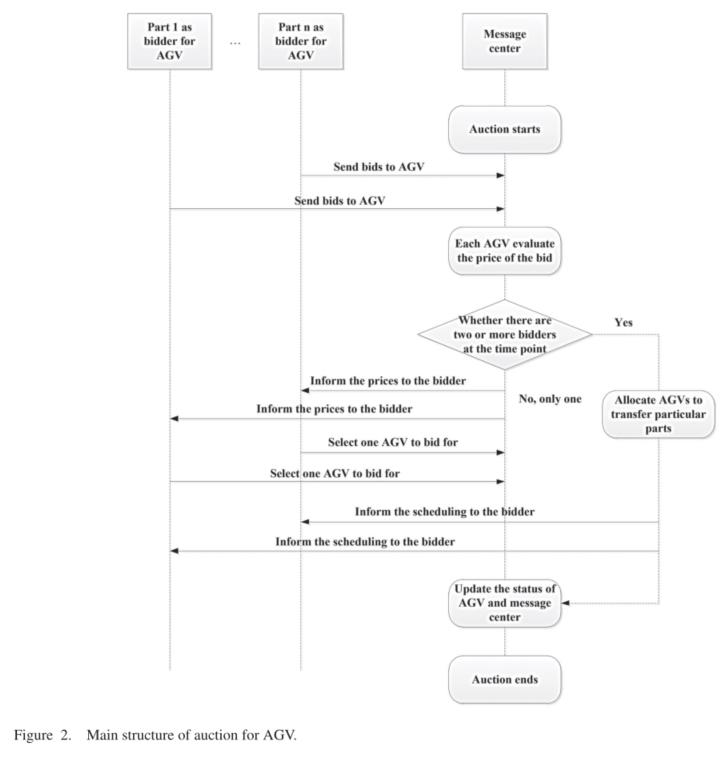
         拍卖AGV的主要框架：

        当一个零件想要竞标AGV的时隙时，它将包含它希望AGV到达的时间以及何时开始将其转移到下一台机器。要确定这些信息，首先需要确定AGV的(计划)路线。现在，问题出现了，如何确定AGV的路线。当AGV得到第一个运输任务(部件)时，它将直接从原来的位置移动。随着任务的增多，AGV需要决定何时装入(特定)部件以及何时卸货。AGV将根据AGV的当前位置和部件、部件的目的地位置、自由空间大小和规划路线来选择时间。

 3.2.2 样例

        表1就是一个带运输能力约束的M-CPS问题，其中AGV数量为1，容量为2.

         于是，AGV在CELL之间的运输路线如下：

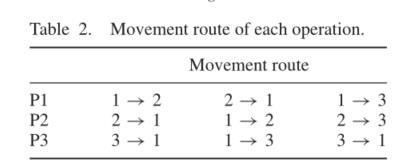
        AGV的最终每个时间短的 

         得到初始解AGV的各时间节点和闲余空间：

        Gantt图如下：

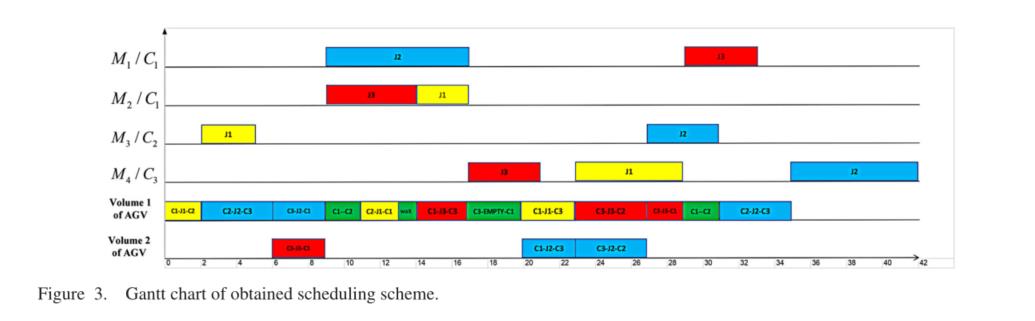         机器拍卖：

                当操作完成生产安排时，它将打开机器，调用该资源处理。如果机器状态不可用，则将拒绝操作请求，并且操作将持续联系机器，直到机器可用于响应请求。之后，拍卖将开始。然后，拍卖将在拍卖人响应请求时开始。我们处理一个参数ASL，即每次拍卖中(开放)时隙的长度。在提交修改后的投标后，拍卖人将决定谁将获胜，并且存在两种情况：(1)只有一个总成本最高的投标人；(2)多个总成本相同的投标人。对于第一种情况，只有一个投标人可以赢得拍卖；对于第二种情况，拍卖人将以相同的总成本估算不同投标人的投标时隙，如果它们之间存在冲突，被选中的投标人将继续按照上述方式修改竞价，以拍卖时隙，直到一个投标人赢得拍卖。否则，所有总成本最高的投标人都将成为赢家。

3.2.3 改进的析取图模型

        基于拍卖方法，我们可以得到有容量约束的M-CPS问题的可行解。

        下图表示的是AGV容量为1的JS-AGV析取图：

         由于AGV的容量等于1，所以析取图模型可以描述JS-AGV问题。一旦AGV装载了部件，它必须立即转移以卸载该部件。然而，在我们提出的问题中，当AGV的载客量大于1时，AGV在装载零件后可能不会立即转移卸货，如何用析取图模型来描述这一点？同样，由于AGV的容量大于1，当AGV移动到机器上时，如何区分AGV是装卸零件呢？

        为了解决这一问题，我们将运输任务分为两部分：装卸任务。例如，T13将被描述为L13和U13，分别表示装载和卸载O13。

4 实验

        实验为La01-La40的改编