⭐K-Means和DBSCAN聚类算法——理论结合代码的实现
Posted 土味儿大谢
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了⭐K-Means和DBSCAN聚类算法——理论结合代码的实现相关的知识,希望对你有一定的参考价值。
文章目录
一、基本概念
聚类本质上是一个贴标签的过程
聚类与分类的区别
- 分类:监督学习,有限类别中的某一类
- 聚类:无监督学习,不依赖预先定义的类或带类标记的训练实例需要由聚类学习算法自动确定标记 。聚类是一种探索性的分析,聚类分析所使用方法的不同,用的特征不同,常常会得到不同的结论
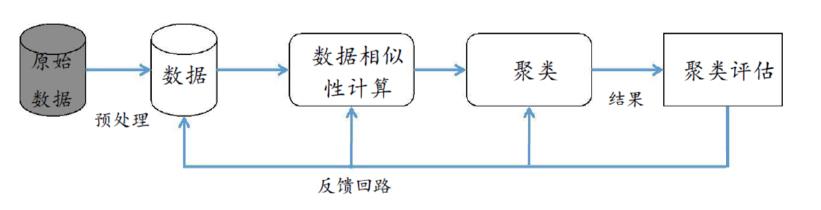
聚类基本流程
-
对数据进行表示和预处理 包括数据清洗、特征选择或特征抽取
-
给定数据之间的相似度或相异度及其定义方法
-
根据相似度 对数据进行划分 即聚类
-
对聚类结果进行评估
常见聚类方法
| 基于划分聚类算法 | K-means,K-medoids,CLARA |
| 基于层次聚类算法 | BIRCH,CURE 等 |
| 基于密度聚类算法 | DBSCAN,OPTICS 等 |
| 基于网格的聚类算法 | STING,WaveCluster 等 |
| 基于神经网络的聚类算法 | 自组织神经网络SOM |
| 基于统计学的聚类算法 | COBWeb,AutoClass 等 |
二、K-Means
这里的K表示要把数据聚成几个类
基本思想:将每一个样本分配给最近中心(均值)所属的类
Kmeans:基于距离的聚类
- 自定义聚类数据:
- 肘部法则
- 轮廓系数
- 对初始质心敏感:多次随机初始化
- 适合凸数据集
2.1 基本步骤与流程
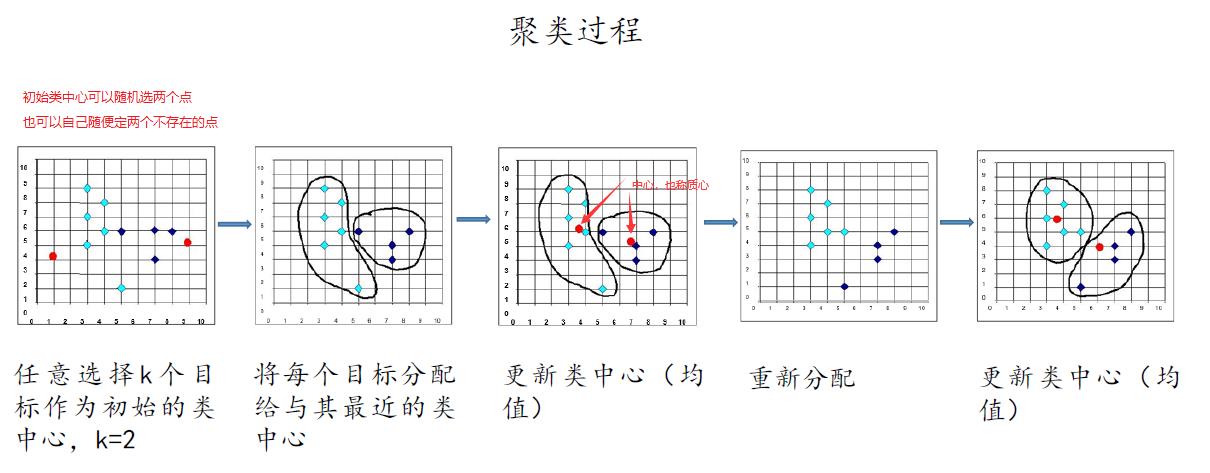
算法步骤:
- 先从没有标签的元素集合 A 中随机取 k 个元素作为 k 个子集各自的中心
- 分别计算剩下的元素到 k 个子集中心的距离 将这些元素分别划归到距离最近的子集
- 根据聚类结果 重新计算中心 子集中所有元素各个维度的算数平均数
- 将集合 A 中全部元素按照新的中心再重新聚类
- 重复以上步骤 直到聚类的结果不再发生变化
2.2 代码实现
2.2.1 手写python代码实现
kmeans.txt
1.658985 4.285136
-3.453687 3.424321
4.838138 -1.151539
-5.379713 -3.362104
0.972564 2.924086
-3.567919 1.531611
0.450614 -3.302219
-3.487105 -1.724432
2.668759 1.594842
-3.156485 3.191137
3.165506 -3.999838
-2.786837 -3.099354
4.208187 2.984927
-2.123337 2.943366
0.704199 -0.479481
-0.392370 -3.963704
2.831667 1.574018
-0.790153 3.343144
2.943496 -3.357075
-3.195883 -2.283926
2.336445 2.875106
-1.786345 2.554248
2.190101 -1.906020
-3.403367 -2.778288
1.778124 3.880832
-1.688346 2.230267
2.592976 -2.054368
-4.007257 -3.207066
2.257734 3.387564
-2.679011 0.785119
0.939512 -4.023563
-3.674424 -2.261084
2.046259 2.735279
-3.189470 1.780269
4.372646 -0.822248
-2.579316 -3.497576
1.889034 5.190400
-0.798747 2.185588
2.836520 -2.658556
-3.837877 -3.253815
2.096701 3.886007
-2.709034 2.923887
3.367037 -3.184789
-2.121479 -4.232586
2.329546 3.179764
-3.284816 3.273099
3.091414 -3.815232
-3.762093 -2.432191
3.542056 2.778832
-1.736822 4.241041
2.127073 -2.983680
-4.323818 -3.938116
3.792121 5.135768
-4.786473 3.358547
2.624081 -3.260715
-4.009299 -2.978115
2.493525 1.963710
-2.513661 2.642162
1.864375 -3.176309
-3.171184 -3.572452
2.894220 2.489128
-2.562539 2.884438
3.491078 -3.947487
-2.565729 -2.012114
3.332948 3.983102
-1.616805 3.573188
2.280615 -2.559444
-2.651229 -3.103198
2.321395 3.154987
-1.685703 2.939697
3.031012 -3.620252
-4.599622 -2.185829
4.196223 1.126677
-2.133863 3.093686
4.668892 -2.562705
-2.793241 -2.149706
2.884105 3.043438
-2.967647 2.848696
4.479332 -1.764772
-4.905566 -2.911070
import numpy as np
import random
import matplotlib.pyplot as plt
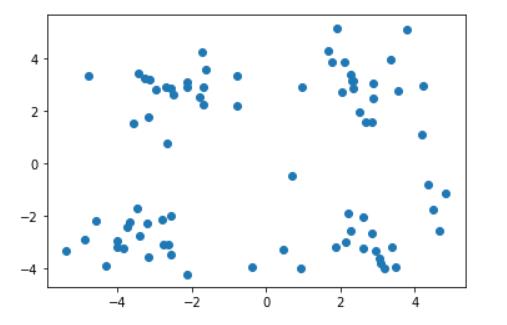
data = np.genfromtxt('kmeans.txt',delimiter=' ')
plt.scatter(data[:,0],data[:,1]) #散点图
plt.show()
#计算两个向量的距离,用的是欧几里得距离
def euclDistance(vector1, vector2):
return np.sqrt(sum((vector1-vector2)**2))#
#随机生成初始的质心。只选一次就行
def initCentroids(data, k): #k=4
centroids=random.sample(data.tolist(),k) #不能对数组采,转化为列表,得到4个列表
return np.array(centroids) #转换回数组,得到4×2的质心
# 主代码,迭代,传入数据和k值,k=4
def kmeans(data, k): #data为所有数据,k需要指定
# 计算样本的个数
numSamples = data.shape[0] #80
# clusterData样本的属性,行是代表各个样本,第一列保存样本属于哪个簇,第二列保存样本跟它所属簇的距离
clusterData = np.zeros((numSamples, 2)) #新建为0的数组
# 初始化质心
centroids = initCentroids(data, k) #4*2
# 决定质心是否要改变,决定是否要继续迭代
clusterChanged = True #控制是否循环
while clusterChanged: #次数不确定所以用while循环
clusterChanged = False
# 循环每一个样本
for i in range(numSamples): #80,对所有的样本点
# 最小距离
minDist = 100000.0
# 定义样本所属的簇
minIndex = 0
# 循环计算每一个质心和样本的距离
for j in range(k): # 4,求每个样本点到4个质心的距离
# 计算距离 选最小的
distance = euclDistance(centroids[j,:],data[i,:])
if distance < minDist:
# 更新最小距离
minDist = distance
# 更新样本所属的簇
minIndex = j
# 更新样本保存的最小距离
clusterData[i,1] = distance
# 每算完一个样本点都要看一下标签。如果样本所属的簇发生改变
if clusterData[i,0] != minIndex:
clusterChanged = True
# 更新样本的簇
clusterData[i,0] = minIndex
# 所有样本贴上标签后更新质心
for j in range(k):#0,1,2,3
# 第j个簇所有的样本点
pointsInCluster = data[clusterData[:,0]==j]
# 计算质心
centroids[j,:] = np.mean(pointsInCluster,axis=0)
return centroids, clusterData
# 设置k值
k = 4
# centroids簇的中心
# clusterData样本的属性,行是代表各个样本,第一列保存样本属于哪个簇,第二列保存样本跟它所属簇的距离
centroids,clusterData = kmeans(data, k)
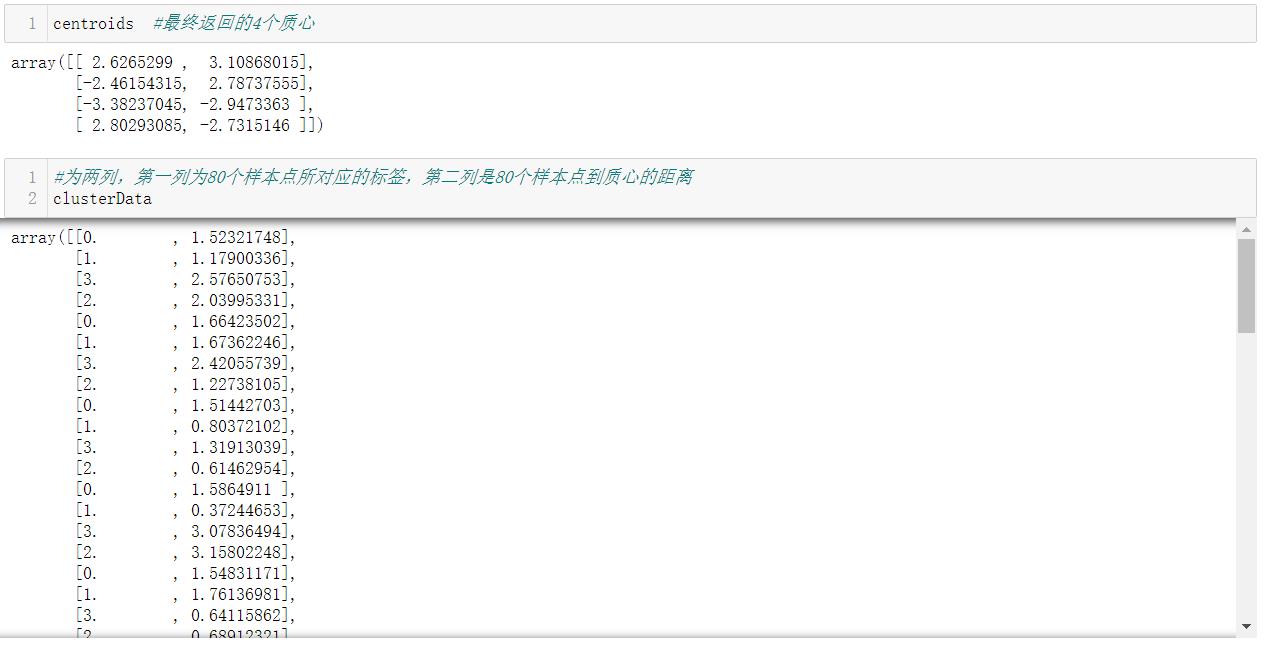
显示聚类结果:
#可视化函数
def showCluster(data, k, centroids, clusterData):
#画样本点
numSamples, dim = data.shape #80,2
mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', '<r', 'pr'] #不同的簇类样本点用不同mark
for i in range(numSamples): #所有样本点
markIndex = int(clusterData[i,0]) #簇头,0,1,2,3
plt.plot(data[i, 0], data[i, 1], mark[markIndex])
#画质心
mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', '<b', 'pb']
for i in range(k): #画质心
plt.plot(centroids[i, 0], centroids[i, 1], mark[i], markersize = 12)
plt.show()
showCluster(data, k, centroids, clusterData) #画图
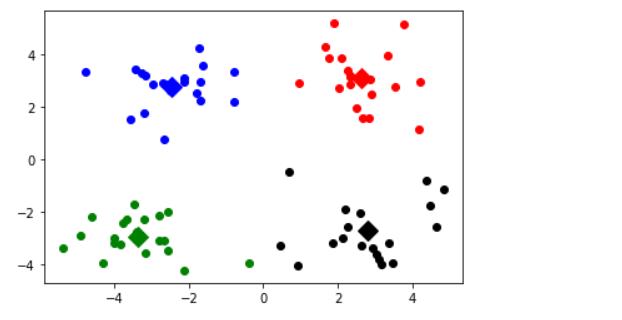
#做预测,执行的是分类
x_test = [0,1]
np.argmin(np.sqrt((x_test - centroids)**2).sum(axis=1)) #返回最小值所对应的索引下标

2.2.2 算法优化
2.2.2.1 多次随机初始化
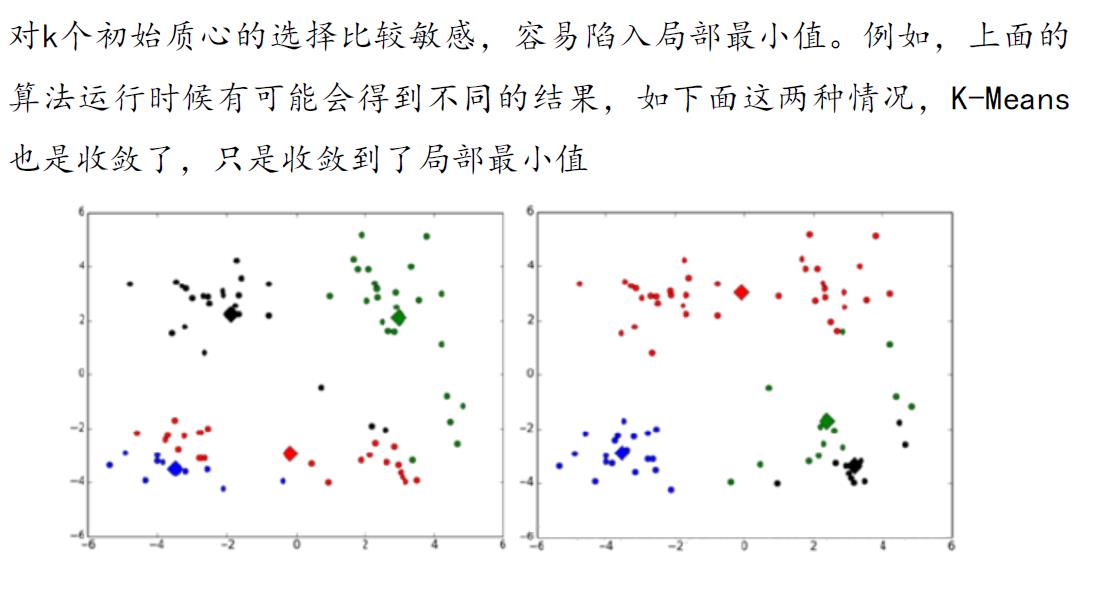
使用多次随机初始化,计算每一次建模得到代价函数的值,选取代价函数最小结果作为聚类结果
# 设置k值
k = 4
min_loss = 10000
min_loss_centroids = np.array([]) #最小loss对应的质心
min_loss_clusterData = np.array([]) #最小loss对应的clusterData
for i in range(50): #随机50次
centroids,clusterData = kmeans(data, k) #每次都会得到质心和clusterData。要clusterData内的数据最小
loss = sum(clusterData[:,1]**2)/data.shape[0] #误差平方和 SSE
if loss < min_loss:
min_loss = loss
min_loss_centroids = centroids
min_loss_clusterData = clusterData
centroids = min_loss_centroids #最终的质心
clusterData = min_loss_clusterData #最终的clusterData
showCluster(data, k, centroids, clusterData)
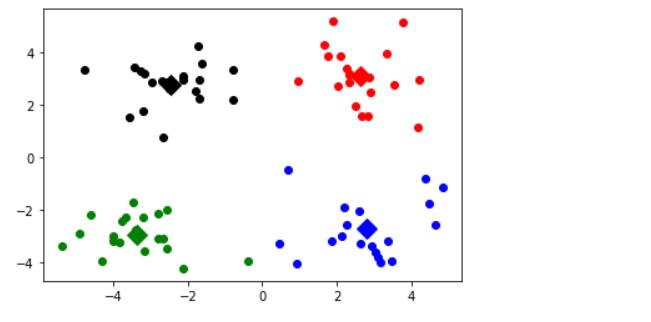
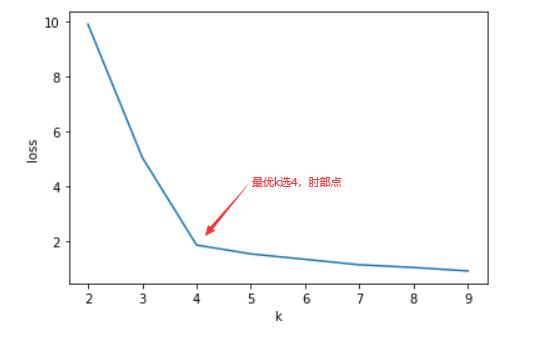
2.2.2.2 使用肘部法则确定k
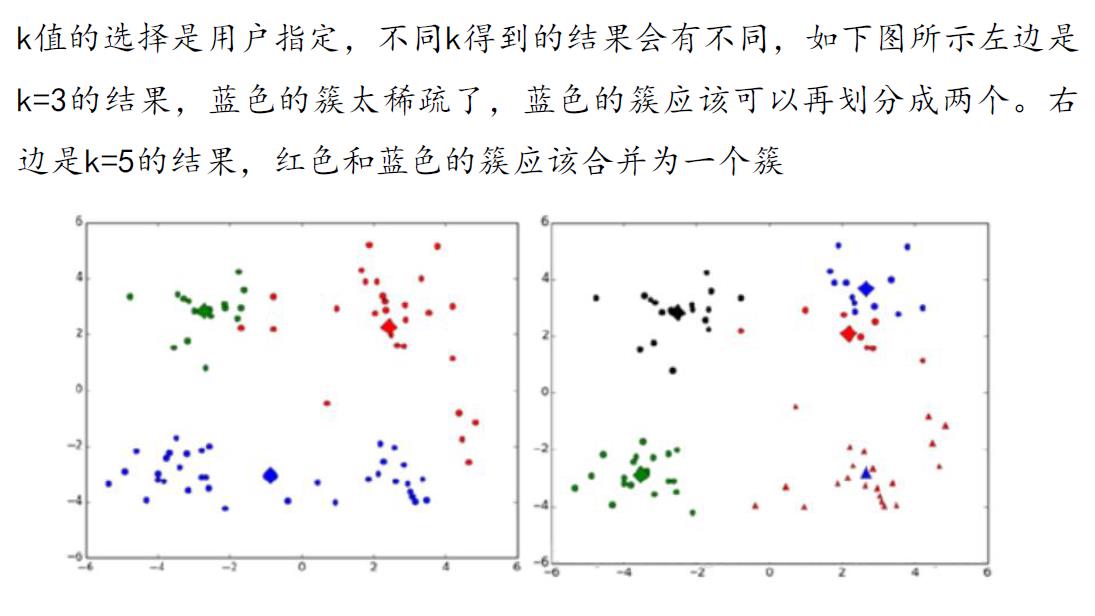
使用肘部法则或轮廓系数来选择 k 的值
list_loss = [] #损失函数,SSE
for k in range(2,10): #尝试不同的k值
min_loss = 10000
min_loss_centroids = np.array([])
min_loss_clusterData = np.array([])
#解决初始质心选择
for i in range(50): #每个k都迭代50次
centroids,clusterData = kmeans(data, k)
loss = sum((clusterData[:,1])**2)/data.shape[0]
if loss < min_loss:
min_loss = loss
min_loss_centroids = centroids
min_loss_clusterData = clusterData
list_loss.append(min_loss)
plt.plot(range(2,10),list_loss)
plt.xlabel('k')
plt.ylabel('loss')
plt.show()
2.2.3 sklean中的kmeans
https://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html#sklearn.cluster.KMeans

代码实现:
from sklearn.cluster import KMeans
import numpy as np
import matplotlib.pyplot as plt
# 载入数据
data = np.genfromtxt('kmeans.txt',delimiter=' ')
k = 4
model = KMeans(n_clusters=k) #创建模型
model.fit(data) #聚类结束

model.cluster_centers_ #四个质心

model.labels_ #样本所对应的标签

model.predict(data) #预测,分类

model.n_iter_ #迭代次数

model.inertia_ #SSE,簇内平方误差和
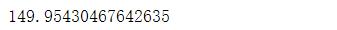
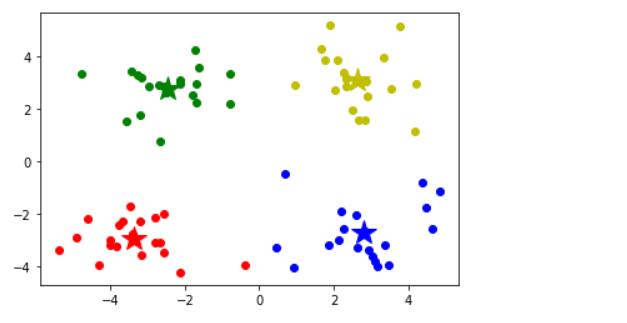
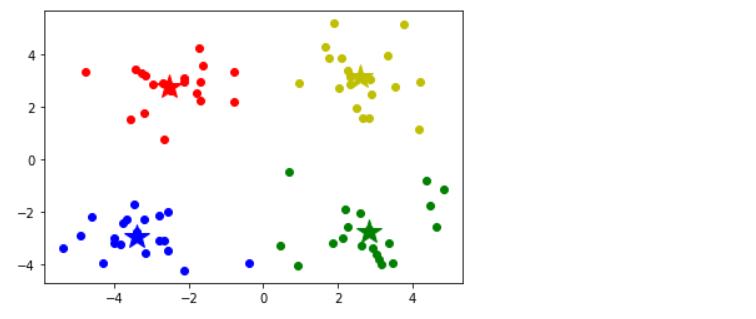
#画图
centers=model.cluster_centers_ #质心
# 画样本点
mark = ['or','ob','og','oy']
for i,d in enumerate(data):
plt.plot(d[0],d[1],mark[model.labels_[i]])
# 画质心
mark = ['*r','*b','*g','*y']
for i,center in enumerate(centers):
plt.plot(center[0],center[1],mark[i],markersize=20)
plt.show()
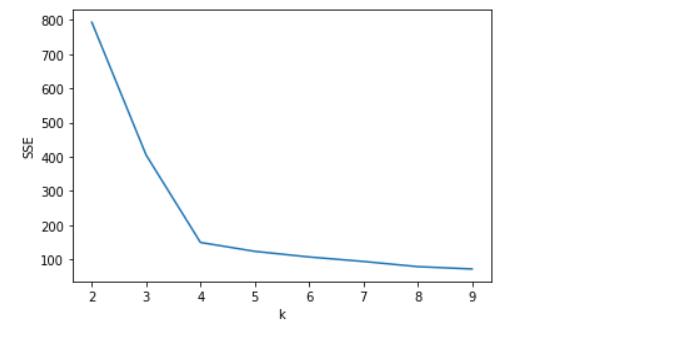
2.2.3.1 肘部法则优化k
SSE=[]
for k in range(2,10): #优化n_clusters参数
model = KMeans(n_clusters=k)
model.fit(data)
SSE.append(model.inertia_) #SSE
plt.plot(range(2,10),SSE)
plt.xlabel('k')
plt.ylabel('SSE')
plt.show()
2.2.3.2 轮廓系数

from sklearn import metrics
silhouette_all=[] #轮廓系数
for k in range(2,10):
model = KMeans(n_clusters=k) #聚类
model.fit(data)
labels = model.labels_ #每个样本的标签
silhouette_score = metrics.silhouette_score(data, labels) #轮廓系数;所有样本点的轮廓系数的平均值
silhouette_all.append(silhouette_score)
plt.plot(range(2,10),silhouette_all) #k和轮廓系数关系
plt.xlabel('k')
plt.ylabel('silhouette_score')
plt.show()
#选最高的k值聚类会比较好

2.2.4 MiniBatchKMeans
样本数比较多的时候,收敛比较慢。就要用到这种算法进行优化

https://scikit-learn.org/stable/modules/generated/sklearn.cluster.MiniBatchKMeans.html#sklearn.cluster.MiniBatchKMeans

from sklearn.cluster import MiniBatchKMeans
import numpy as np
import matplotlib.pyplot as plt
# 载入数据
data = np.genfromtxt('kmeans.txt',delimiter=' ')
data.shape #数据比较少,看不出什么性能变化
# 设置k值
k = 4
model = MiniBatchKMeans(n_clusters=k,batch_size=100)
model.fit(data)

centers = model.cluster_centers_
centers

predictions = model.predict(data)
predictions

# 画样本点
mark = ['or','ob','og','oy']
for i,d in enumerate(data):
plt.plot(d[0],d[1],mark[predictions[i]])
# 画分类中心点
mark = ['*r','*b','*g','*y']
for i,center in enumerate(centers):
plt.plot(center[0],center[1],mark[i],markersize=20)
plt.show()
三、DBSCAN(基于密度)
3.1 基本概念
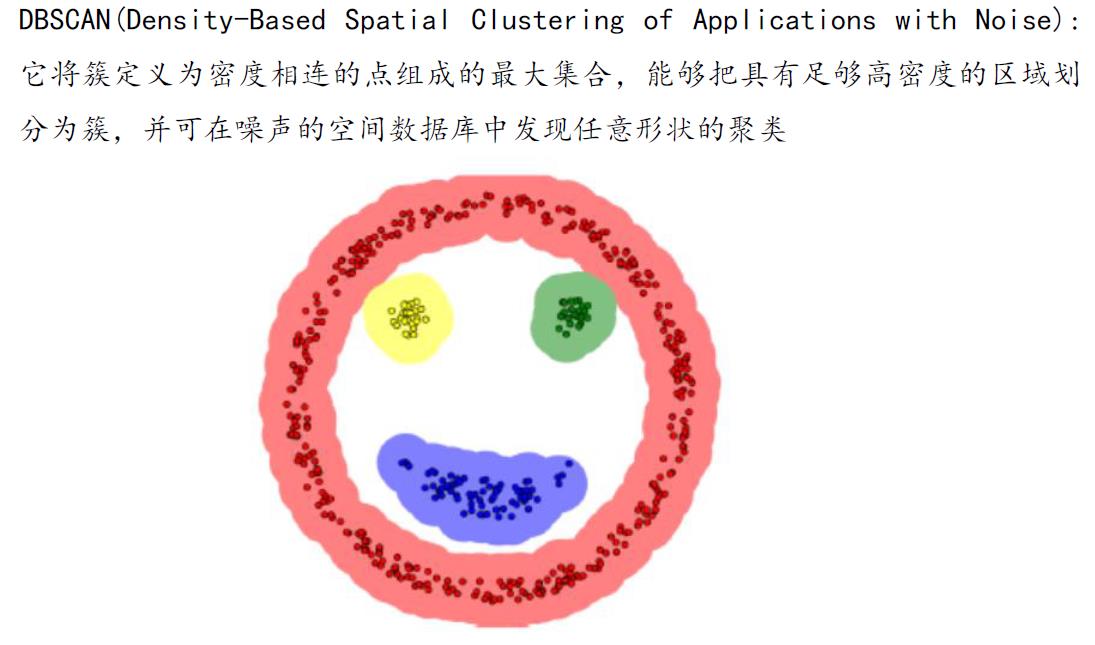
DBSCAN 中的几个定义:
-
Ε 邻域:给定对象半径为 Ε 内的区域称为该对象的 Ε 邻域
-
核心对象:如果给定对象 Ε 邻域内的样本点数大于等于 Min-points 则称该对象为核心对象
-
直接密度可达:对于样本集合 D, 如果样本点 q 在 p 的 Ε 邻域内,并且 p 为核心对象,那么 p 到 q 直接密度可达
-
密度可达:对于样本集合 D 给定一串样本点 p 1,p 2 pn,p=p1,q=pn,假如pi-1 到 pi 直接密度可达,那么对象 p 到 q 密度可达
-
密度相连:存在样本集合 D 中的一点 o ,如果对象 o 到对象 p 和对象 q 都是密度可达的,那么 p 和 q 密度相联
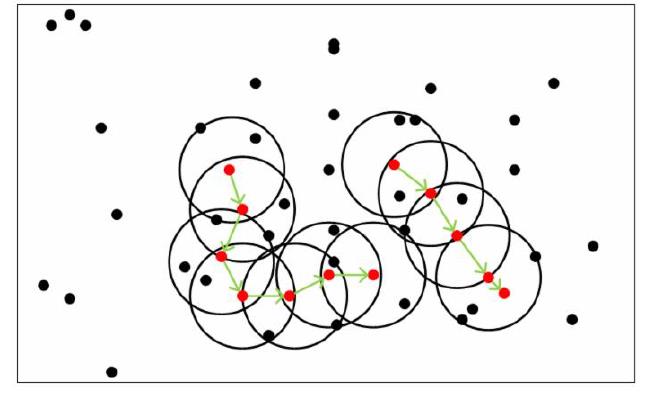
DBSCAN 密度聚类思想:由密度可达关系导出的最大密度相连的样本集合,即为我们最终聚类的一个类别,或者说一个簇
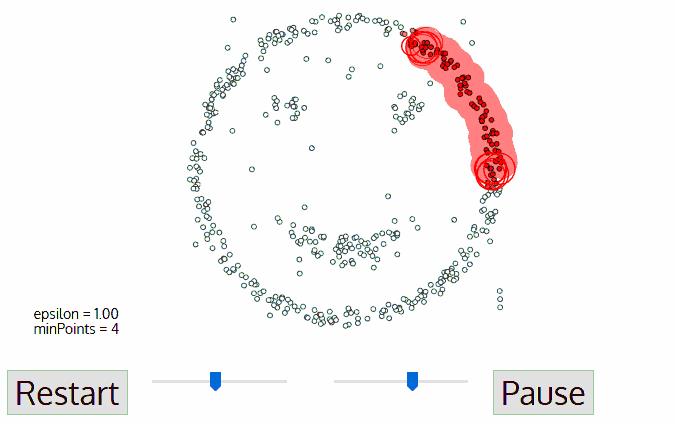
算法步骤:
- 指定合适的 E 和 Min-points
- 计算所有的样本点,如果 p 的 E 邻域里有超过 Min-points 个点,则创建一个以 p 为核心点的新簇
- 反复寻找这些核心点直接密度可达(之后可能是密度可达 )的点,将其加入到相应簇 对于核心点发生“密度相连”状况的簇,给予合并
- 当没有新的点可以被添加到任何簇时,算法结束
3.2 凸数据集
from sklearn.cluster import DBSCAN
import numpy as np
import matplotlib.pyplot as plt