数据结构之堆以及topk问题

Posted 2021-09-19 捕获一只小肚皮

文章目录

• 前言
• 堆的结构化
• 定义堆
• 堆的各种操作方法
• 堆操作之初始化
• 堆操作之销毁空间
• 堆操作之入堆
• 堆操作之出堆
• 堆操作之判空
• 堆操作之获取堆顶
• 堆操作之获取大小
• 堆结构练习:获取前k个最小或最大元素

前言

博主上一小节动图演示堆讲到了通过堆的特性进行堆排序,今天博主将要提到的就是详细了解堆,以及实现堆操作

---

堆的结构化

既然我们知道是堆是一种特殊的二叉树,并且是用顺序表进行实现的,那么我们便尝试着用顺序表进行实现堆的高级操作,比如入堆,出堆,初始化等等.

---

定义堆

既然是用顺序表实现堆,那么我们便需要借助顺序表,代码如下:

typedef int HeapDataType;
typedef struct heap      //堆
{
    HeapDataType* num;     //数组
    int size;
    int capacity;
}heap;

---

堆的各种操作方法

既然堆是一种数据结构,那么它同样与其他数据结构一样,具有增删改查等功能,所以我们现在先声明各种方法,后面再一一实现各个方法.

堆的初始化声明:

//堆初始化主要负责把数组num中的数字转移到pheap->num中,然后把pheap->num中的数据转换为堆的逻辑结构
void HeapInit(heap* pheap,HeapDataType* num,int n);   //n是数组长度

堆的销毁

//当此堆不再使用以后就要销毁空间
void HeapDestroy(heap* pheap);

数据载入堆

//此函数作用是把新数据载入堆,并且还要保持堆的结构不被破坏
void HeapPush(heap* pheap,int n);

删除堆顶元素

//此函数作用是为了删除堆顶元素并且堆结构不能被破坏,最后还需要返回所删除的元素
HeapDataType HeapPop(heap* pheap);

判断堆中数据是否为空

bool HeapEmpty(heap* pheap);

获取堆顶元素

HeapDataType HeapTop(heap* pheap);

获取堆的大小

int HeapSize(heap* pheap);

---

此外,没有看博主上一节文章动图演示堆排序的小伙伴先看下堆排序哦,下面博主会直接贴出向下调整算法,不再解释了哦~~

向下调整算法:

void AdjustDown(int num[], int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child + 1 < n && num[child] < num[child + 1])
		{
			child++;
		}

		if (num[parent] < num[child])
		{
			Swap(&num[parent], &num[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

---

堆操作之初始化

堆初始化主要负责把数组num中的数字转移到pheap->num中,然后把pheap->num中的数据转换为堆的逻辑结构

所以涉及的内容为数组拷贝(挨个赋值也可以),动态空间开辟,向下调整算法进行建堆

void HeapInit(heap* pheap, HeapDataType* num, int n)
{
	assert(pheap);
	//第一步,开辟空间
	HeapDataType* tmp = (HeapDataType*)malloc(sizeof(HeapDataType) * n);
	if (tmp == NULL)
	{
		printf("空间开辟失败,抱歉!\\n");
		exit(-1);
	}
	pheap->num = num;
	pheap->size = pheap->capacity = n;   //初始化数组大小和容量

	//第二步,拷贝数组.
	memcpy(pheap->num, num, sizeof(HeapDataType) * n);

	//第三步,建堆.
	for (int parent = (n - 1 - 1) / 2; parent >= 0; parent--)
	{
		AdjustDown(pheap->num, n, parent);
	}
}

---

堆操作之销毁空间

堆销毁空间很简单,直接free掉num就行

void HeapDestroy(heap* pheap)
{
	assert(pheap);
	free(pheap->num);
	pheap->num = NULL;
}

---

堆操作之入堆

该函数的要求是数据必须进入堆,并且不能毁掉堆的特性.大家想想有什么办法可以解决?

答案是进行向上调整,过程如下图(以小堆为例子):

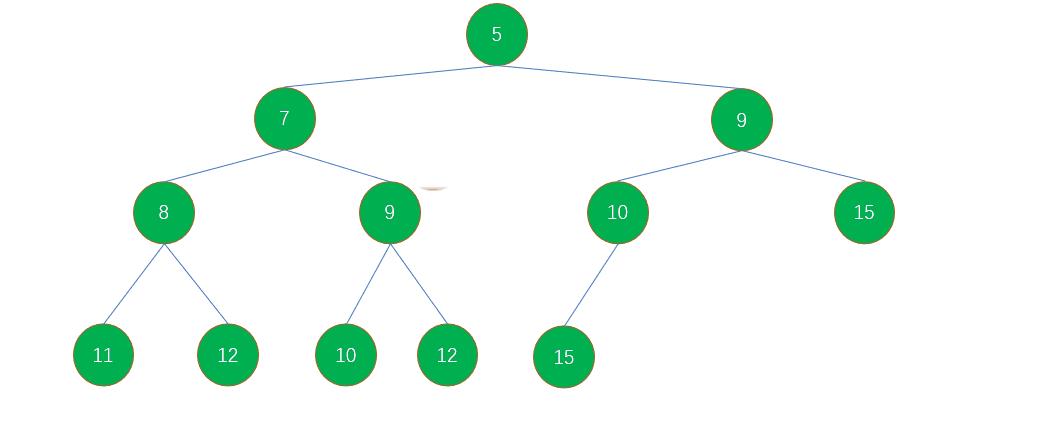
观察上图,我们发现向上调整的步骤是:

• 数据首先载入最后
• 与其双亲结点进行比较,如果比双亲结点小,就交换其值,一直不断重叠
• 如果该数据比双亲结点值大,就结束调整;如果当child等于0,就结束调整

所以代码如下:

void HeapPush(heap* pheap, int n)
{
	assert(pheap);

	//第一步,需要检查堆空间是否足够继续存储新数据,不足时候句增加空间,这一步很多人总是忽略
	if (pheap->size == pheap->capacity)
	{
		HeapDataType* tmp = (HeapDataType*)realloc(pheap->num, pheap->capacity * 2 * sizeof(HeapDataType));
		if (tmp == NULL)
		{
			printf("空间不足,系统尝试增容,但是抱歉,增容失败.\\n");
			exit(-1);
		}
		pheap->capacity *= 2;
	}

	//数据入堆
	pheap->num[pheap->size] = n;
	pheap->size++;

	//开始向上调整
	AdjustUp(pheap->num, pheap->size-1);
}

上面我们可以把向上调整写成一个函数

void AdjustUp(HeapDataType num[], int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)   //主要动的就是child位置,所以child>0
	{
		if (num[child] < num[parent])
		{
			Swap(&num[child], &num[parent]);   //自己写一个交换函数
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

---

堆操作之出堆

该函数的作用是删除堆顶元素,并且不能毁坏堆结构,大家想想有什么办法呢?

答案是,借助堆排序的思想,先把堆顶元素与最后一个元素交换,然后不管最后一个元素,重新进行向下调整.

仍然以小堆为例,看下图演示:

HeapDataType HeapPop(heap* pheap)
{
	assert(pheap);
	assert(!HeapEmpty(pheap));
	//保存需要删除的值
	HeapDataType return_value = pheap->num[0];

	//交换首位
	Swap(&pheap->num[0], &pheap->num[pheap->size - 1]);
	pheap->size--;   //当size减一就代表着已经删除了最后一个值.

	//向下调整
	AdjustDown(pheap->num, pheap->size, 0);

	//返回
	return return_value;
}

---

堆操作之判空

bool HeapEmpty(heap* pheap)
{
    assert(pheap);
    return pheap->size == 0;
}

---

堆操作之获取堆顶

HeapDataType HeapTop(heap* pheap)
{
    assert(pheap);
    assert(!HeapEmpty(pheap));
    return pheap->num[0];
}

---

堆操作之获取大小

int HeapSize(heap* pheap)
{
    assert(pheap);
    return pheap->size;
}

堆结构练习:获取前k个最小或最大元素

题目:

假设有数组num,其内容的定义如下:

#include <time.h>
int main()
{
    int num[10000] = {0};
	srand(time(NULL));
    for(int i = 0;i<10000;i++)
    {
        num[i] = rand() % 10000;  //保证数组中每个元素都是小于10000;
    }
    
    for(int i = 0;i<10;i++)
    {
        num[rand() % 10000] = rand()%10 + 10001;  //随机给数组赋值10个大于10000的数.
    }
}

要求:写一个算法,求出该数组前10个大于10000的数.

而这我们就可以利用堆的特性,因为堆的最值永远在堆顶,所以每次获取删除堆顶的元素就行

void  SetNarry(int num[])
{
    srand(time(NULL));
    for (int i = 0; i < 10000; i++)
    {
        num[i] = rand() % 10000;  //保证数组中每个元素都是小于10000;
    }

    for (int i = 0; i < 10; i++)
    {
        int ret = 0;
        num[ret = rand() % 10000] = rand() % 10 + 10001;  //随机给数组赋值10个大于10000的数.
    }
}

int main()
{
    heap hp = { 0 };
    int  num[10000] = { 0 };

    SetNarry(num); //给数组赋值

    HeapInit(&hp, num,10000); //变成堆,初始化函数里面的向下调整算法注意修改成大堆算法哦

    for (int i = 0; i < 10; i++)
    {
        printf("%d ", HeapPop(&hp));
    }
    return 0;
}

测试:

成功

我们分析下这种算法的时间复杂度是多少?

建堆时间复杂度为O(N) , 删除堆顶时间复杂度复杂为O(k * logN),所以最后时间复杂度为O(N+k * logN).

现在我们对数据升级了,假设有100亿个数据,电脑内存存不下了,请问该怎样利用堆特性解决?

这是一道思考题,博主就不赘述了,大家仔细想想哦~~