LeetCode最小栈问题的最优解法+代码实现

Posted 2021-09-19 xiao zhou

LeetCode最小栈问题的最优解法+代码实现

• 题目描述
• 思路一（错误的）
• 思路二（时间复杂度O（1）、空间O（N））
• • 初版思想
  • • 代码实现：
  • 进阶思想
  • • 代码实现：
• 思路二（最优解：时间复杂度O（1）、空间O（1））
• • 算法思想
  • • 代码实现：
  • 总结
• 综上

xxxx最近做了一道LeetCode中的一道题。 最小栈，这道题其实是一个简单级别的题目，但是如果深究这道题，我觉得还是可以到达一个很深的层次。因为这道题如果想解决不算难，但是如果追求时间、空间上的极致，确实需要一定的思考与算法基础。

题目描述

xxxx简单来说，设计一个栈，除了基本的push、pop、top操作，还需要设计一个直接可以获取栈中元素最小值的接口。

思路一（错误的）

xxxx我估计大多数人都会像我一样，牺牲栈中第一个位置，或者创建一个成员变量，用来存储最小值。当push数据的时候就与这个最小值进行比较，如果push的新数据小于最小值，那么就更新最小值。
xxxx但是这种想法是错误的。举一个例子来印证这个错误。
错误原因：假如栈中的数据是{ 2,1,0 }，那么此时最小值 min=0，当我们pop掉栈顶数据0时，min就要被更新，而更新的话，就要遍历整个栈中数据。而栈中的数据又无法直接遍历，所以这种想法是错误的。

思路二（时间复杂度O（1）、空间O（N））

初版思想

xxxx有一个很好的思路，就是额外使用一个辅助栈，这个辅助栈就是存储最小值。每次调用getMin时，直接取辅助栈的栈顶数据就是当前栈中数据的最小值
分析原因:其实这也依赖了栈的后进先出的原理。这个最后再印证。
1、首先，push第一个数据a后，栈中只有一个数据，当然最小的数据就是它自己，所以我们在辅助栈中push该数据a，表明栈中该位置及以前所有数据中a是最小的。
2、然后我们再push第二个数据b，
（1）如果b>a，说明在栈中所有数据中a仍然是最小的，那么在辅助栈中仍然push进a，说明，在该位置及以前所有数据中，仍然是a最小
（2）如果b<=a，说明b是目前栈中所有数据中最小的数，那么就要push进b，最小值就更新成b
3、重复（2）步骤知道数据push结束。。。。
4、解释为何依赖了栈的后进先出的特点：在push数据的时候，我们就可以得到插入每一个数字之后，最小值。在pop数据时，由于最先pop出栈的是最新更新的最小值，数据pop，最新更新的最小值也随之出栈，这样剩下的内容就相当于从来没有push过该数据，剩下的栈依然符合既定的结构。
如果不是栈，是队列的话就无法成功，因为pop出的是最先插入的最小值。具体大家可以自己举个例子试验一下，很容易验证！
举一个例子具体阐明：

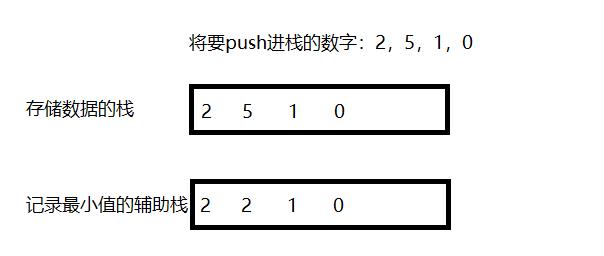
解析
xxxx1、先在栈中push进2，那么栈中只有2这个数字，所以最小值就是2，所以在下面辅助栈中push进2.
xxxx2、再在栈中push进5，5与辅助栈栈顶数据（原先栈中最小数据）2比较，5大，所以最小值不变，那么我们继续在辅助栈中push进2。
xxxx3、再push进1,1与辅助栈栈顶数据（原先栈中最小数据）2比较，1小，那么最小值就更新成1，在辅助栈中push进1。
xxxx4、再在栈中push进0,0与辅助栈栈顶数据（原先栈中最小数据）1比较，0小，那么最小值就更新成0，在辅助栈中就push进0。

代码实现：

class MinStack {
public:
    /** initialize your data structure here. */
    //构造函数，可以不写
    MinStack() {

    }
    
    void push(int val) {
        st.push(val);
        if(help.empty())
        {
            help.push(val);
        }
        else
        {
            //如果新插入数据大于原先辅助栈栈顶数据（原最小数据），那么最小数据不变，还是栈顶数据
            if(val>help.top())
                help.push(help.top());
            //如果小于等于，那么更新最小数据
            else
                help.push(val);
        }
    }
    
    void pop() {
        st.pop();
        help.pop();
    }
    
    int top() {
        return st.top();
    }
    
    int getMin() {
        return help.top();
    }
    //存储数据的栈
    stack<int> st;
    //辅助栈
    stack<int> help;
};

进阶思想

xxxx按照之前的想法，是可以完成的，但是会出现一个问题，那就是如果有大量连续重复的数据，就会导致空间的浪费。
例如：

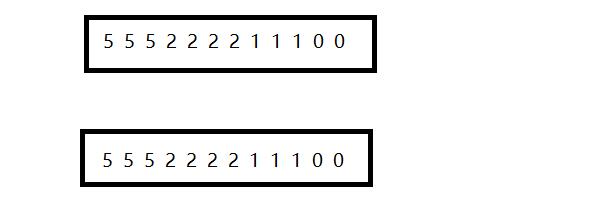
xxxx这个时候我们就想到，如果出现重复的，我们就可以不去push，只写一个。但是就会出现一个问题。例如上面最后push的两个0.下面的辅助栈中只写入一个0，这样当我们pop一个0后，辅助栈也pop一个0.这样导致的结构就是，辅助栈的栈顶元素是1了，但是栈中明明还有更小的0，这就出现了一个问题。因此，为了完成这个任务，我们需要记录，在辅助栈中连续出现了几次相同最小值。

3次5、4次2、3次1、2次0

代码实现：

//创建一个结构体
struct ValueMin
{
	//最小值
    int min;
    //出现次数
    int count;
};

class MinStack {
public:
    /** initialize your data structure here. */
    MinStack() {

    }
    
    void push(int val) {
        st.push(val);
        if(help.empty() || val<help.top().min)
        {
            ValueMin tmp = {val,1};
            help.push(tmp);
        }
        else
        {
            help.top().count += 1;
        }
    }
    
    void pop() {
        int value = st.top();
        st.pop();
        if(!--help.top().count)
            help.pop();
    }
    
    int top() {
        return st.top();
    }
    
    int getMin() {
        return help.top().min;
    }

private:
	//存储数据
    stack<int> st;
    //辅助栈中存储对应最小值及出现次数 
    stack<ValueMin> help; 
};

思路二（最优解：时间复杂度O（1）、空间O（1））

算法思想

xxxx这种方法的话，我们的 stack 栈中，不能存放原始数值，而是应该存放差值，啥是差值？就是存放将要push的数据与最小值的差值。我还是详细一点给大家讲一个案例吧，案例配合代码，应该还是挺好理解的，例如 arr = {3, 2, 2, 4, 0}，那么把这些元素入栈时，stack 栈中元素以及最小值的变化如下：
差值 = 将要入栈元素数值 - 当前最小值

将要入栈元素	差值	入栈后的最小值
3	0（第一个初始化为0）	3
2	2-3=-1	2
2	2-2=0	2
4	4-2=2	2
0	0-2=-2	0

代码实现：

class MinStack {
public:
    /** initialize your data structure here. */
    MinStack() {

    }
    
    void push(int val) {
        if(st.empty())
        {
            //第一个数据，默认为0
            st.push(0);
            min = val;
        }
        else
        {
            long gap = val - min;
            st.push(gap);
            min = gap<0 ? val : min;
        }
    }
    
    void pop() {
        long top = st.top();
        //top<=0,说明要pop掉的数据就是最小值，所以要pop后要更新最小值
        if(top<=0)
        {
            //top = 最后插入的数据-之前的最小值，所以之前的最小值 = 最后插入的数据-top
            //因为top<=0,所以最后插入的值，就是现在最小值
            min = min - top;
        }
        st.pop();
       /* else
        {
            //top大于0，所以产出栈顶元素，最小值不变
            //其实else不需要，我是为了读者理解才写出
            min = min;
        }
        */
    }
    
    int top() {
        long top = st.top();
        if(st.top()<=0)
            return min;
        else
            return (int)(min+top);
        //top = 最后插入的数据-之前的最小值，所以 最后插入的数据=top+之前的最小值
        //因为top>0,所以之前的最小值和当前的最小值相同
            
    }
    
    int getMin() {
        return (int)min;
    }
    stack<long> st;
    long min;
};

注：这里有一个关键的问题，就是，当我们栈st和min都使用int类型时，会有一个整形溢出的bug。如图

为什么会出现这种情况？原因是如下代码

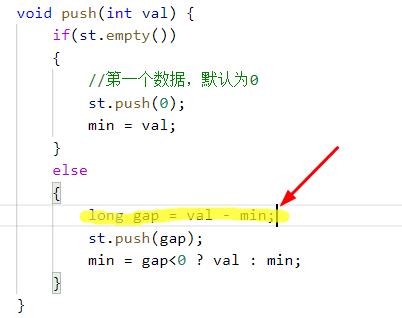
如果gap是int类型，那么gap = val - min时，有情况会使gap整形溢出。
1、val为整形最大值，min为负数时。两者相减，就会使gap溢出
2、val为整形最小值，min为正数时，两者相减，也会使gap溢出
所以，我们先全部用long类型变量存数据，返回时再强转成int类型。

总结

xxxx我们梳理一下最小栈的需要的功能。1、需要像普通栈一样存储、读取数据。2、需要以时间复杂度为O(1)的代价获取最小值。而存差值的方法是如何完成两项任务的呢？首先获取最小值很简单，直接使用min变量来获取，问题就是栈中存的是差值，如何转换成原数值呢？
xxxx答案就是，当存储的差值<=0时，说明将要push进来的值小于等于原先的最小值，最小值就需要更新，因此此时的min就等于该数值。
xxxx当存储的差值>0时，就说明，将要push进来的值是大于原先的最小值的，min还等于原来的值，差值 = 数值 - min。所以数值 = 差值+min。这样就得到了原数值。

综上

xxxx这道题想要过的话，加以思考还是不算难的，如果要求效率极致，就要相处更优秀的算法（思路二）我认为还是比较困难。大家只有多看多练多思考。将知识融会贯通才有可能成为“算法大师”。
xxxx如果大家看完这篇文章有什么感想或者有其他解题思想都可以发表在评论区，或者直接私信我。我们共同学习，共同进步！