[JavaScript 刷题] 算法中的 时间复杂度 和 空间复杂度

Posted 2021-09-18 GoldenaArcher

[javascript 刷题] 算法中的 时间复杂度 和 空间复杂度

• • 时间复杂度
  • 空间复杂度

通常来说判断一个算法的优劣一般会用 时间复杂度 和 空间复杂度 去进行衡量，花的时间越久的算法相对而言是不太偏好使用的算法。

就比如说搬家，一个人如果要搬家就必须先把所有的东西都打包，然后再开车一趟一趟的搬。但是如果 钱(资源 💰) 不成问题的话，就可以雇佣搬家公司，让搬家公司的人来打包，这样一次性就能将所有的东西搬到新的住所。

自己一次次的搬东西就要取决于有多少物品需要搬运了，$n$ 个物品就需要搬运 $n$ 次；对比搬家公司来说，搬家公司一次性将东西搬空只需要搬运 $1$ 次，这两种可以算是简单的 时间复杂度 的对比。现实生活中的算法往往更加的复杂，常见的时间复杂度有 $O(1)$, $O(log(n))$, $O(n)$, $O(nlog(n))$, $O(n^2)$, $O(2^n)$, 以及 $O(n!)$。

图形化展示如下：

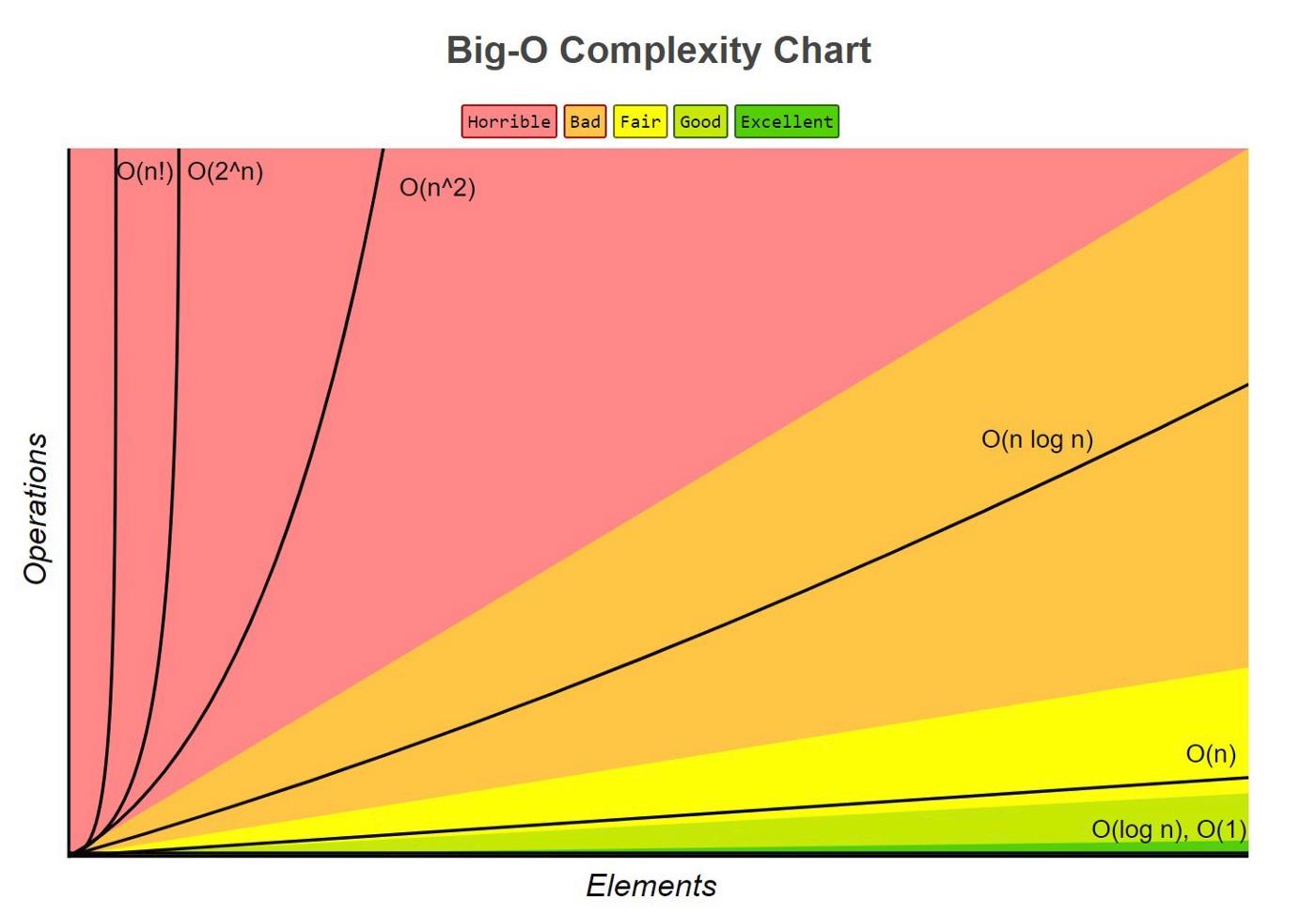
图像资料来源于: Big-O Complexity Chart: http://bigocheatsheet.com/

注意到所有的时间复杂度都以 $O$ 开头进行标注，这也是为什么时间复杂度又被称之为 Big O Notation(大 O 标记法)。

时间复杂度

以上面的图而言，x 轴代表 $n$ 的数量，y 轴代表的则是花费的时间。

在计算时间复杂度的时候，常量 及 非主导项 都是可以被忽略的，因为时间复杂度计算的是当 x 趋近于无穷大的时候，常量 及 非主导项 对比于无穷大的 x，都是没有意义的，因此可以进行简化，只保留 主导项。

另外也可以看到，绿色区域中的 $O(1)$ 和 $O(log(n))$ 在 $n$ 的数量增长的情况下，耗费的时间对比起他的算法来说，显而易见的少。在日常算法中，相对而言 $O(n)$ 是一个比较优的解决方案， $O(log(n))$ 是比较理想的解决方案。

接下来就列举说明一下几种常见的时间复杂度。

• $O(1)$

  指的是该操作花费的时间是一个常量，常见的操作有 使用下标从数组中获取一个值：

  const arr = [1, 2, 3, 4, 5, 6, 7];
  const val = arr[4];
  

  无论 数组的长度(x) 有多少，因为已经知道了 下标(index)，所以获取值的这个操作是一个常量时间。

• $O(log(n))$

  通俗一点的理解就是，每次操作都会使 元素的长度(x) 以对数增长。

  如 二分搜索，每一次的搜索都会使得数组的长度折半，摊开来的做法就是这样的：

  $n,\frac{n}{2},\frac{n}{4},\frac{n}{8},...,1$

  从而推导出 $n\times \frac{1}{2^k}=1$，最终再得出 $k={\log }_{2}n$。

  因为当 元素的长度(x) 趋近于无穷大时，常量可以简化，最终得出二分算法的复杂度为 $O(log(n))$。

  二分算法复杂度在 二分算法 原理 及 复杂度 详解 里有更详细的解释。

• $O(n)$

  应用较多的地方是常见的循环体，一个循环体可以视作一个 $O(n)$，因为循环体内的值都要被遍历：

  for (let index = 0; index < array.length; index++) {
    console.log(array[index]);
  }
  

• $O(nlog(n))$

  这是一个结合了 $O(n)$ 和 $O(log(n))$ 的操作。几个比较有效率的排序算法都是 $O(nlog(n))$ 的复杂度，$O(n)$ 部分在于遍历数组中所有的元素，$O(log(n))$ 部分在于找到元素应当被放置的地方。

• $O(n^2)$,

  最简单的案例在于遍历同一个数组两遍，这是比较常见的暴力解：

  for (let i = 0; i < array.length; i++) {
    // do sth
    for (let j = i; j < array.length; j++) {
      // do sth
    }
  }
  

  一些不是很有效率的排序方法，如冒泡排序、插入排序，也属于时间复杂度为 $O(nlog(n))$ 的范畴。

• $O(2^n)$

  递归的复杂度是 $O(2^n)$，分析之后学到 递归 再讲

空间复杂度

空间复杂度的表达方式和时间复杂度很像，计算方式是一样的，这里就不再重复了。

日常生活中的实现，较为常见的优化是使用 空间 换 时间，例如说缓存就是使用这样的优化方法。