BF与KMP算法的初步认知

Posted 2021-09-18 Booksort

• 算法介绍
• • BF（暴力匹配算法）
  • • 代码实现
  • KMP（模式匹配算法）
  • • 举例分析（逻辑分析）
    • next数组
    • 代码实现next组
    • KMP算法的实现
    • 时间复杂度分析
• 总结

算法介绍

BF（暴力匹配算法）

BF算法，即暴力(Brute Force)算法，是普通的模式匹配算法，BF算法的思想就是将目标串S的第一个字符与模式串T的第一个字符进行匹配，若相等，则继续比较S的第二个字符和 T的第二个字符；若不相等，则比较S的第二个字符和T的第一个字符，依次比较下去，直到得出最后的匹配结果。BF算法是一种蛮力算法。

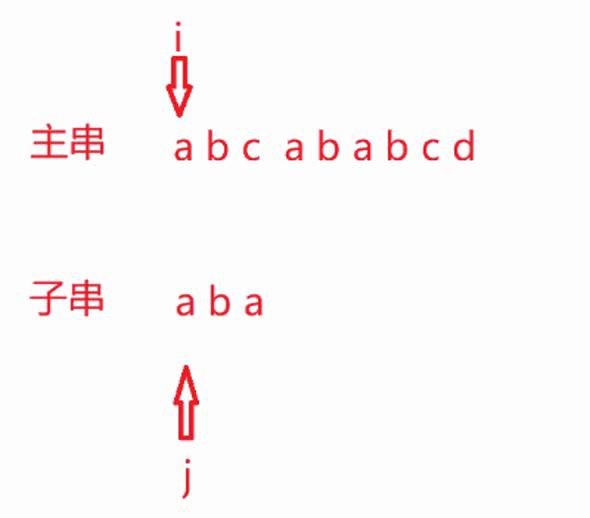
就这样循环往复，进行暴力查找。
有两个分别表示主串和子串的下标，i，j。当元素一样时，a[i]==b[j]满足此条件时， 两个下标都会加加，向后移动一位。如果，a[i]！=b[j]，则，j 会回到子串的起始位置，重新匹配，而 i 会回到刚开始匹配的下一个位置，也就是 i=i-j+1。就这样再次与子串匹配。

代码实现

int BF(string& maistr, string& substr,int pos=0)
{
	int mailen = maistr.size();
	int sublen = substr.size();
	int i = pos;
	int j = 0;
	if (pos >= mailen) return -1;
	if (mailen < sublen) return -1;
	if (mailen == 0 || sublen == 0) return -1;

	while (i < mailen && j < sublen)
	{
		if (maistr[i] == substr[j])
		{
			i++;
			j++;
		}
		else
		{
			i = i - j + 1;
			j = 0;
		}
	}
	return j == sublen ? i - j : -1;
}

举个例子

如果主串中找不到子串，则j会停在除'\\0'以外的任意一个位置，这样只有当主串走完后才会结束循环，这样满足不了条件就只会返回-1
如果j停在'\\0'就代表j==len，就会结束循环。也满足条件。

KMP（模式匹配算法）

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。时间复杂度O(m+n)

KMP算法可以利用匹配失败的信息来减少模式串和主串的匹配次数来加快匹配。而模式串是那种其中有多个重复的子串。

对于KMP算法而言，如果是对非模式串而言，算法时间复杂度会退化严重。

其通过生成一个next数组来完成加快匹配的进程。
但是KMP算法并不像BF算法那样，j会回退回起点，而是回退回next数组中指定的位置。

举例分析（逻辑分析）

此时的情况，如果是BF算法，j回退回0，而i回退回i-j+1。但是太慢了。

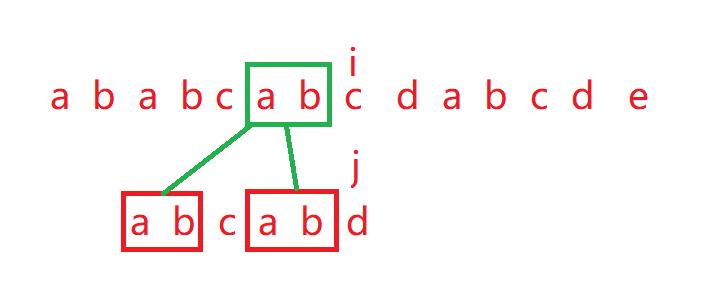
这子串与主串中有一样的。而我们可以知道，当 j走到了某一位置，而该位置前面字符的必定与主串中的字符是匹配的。

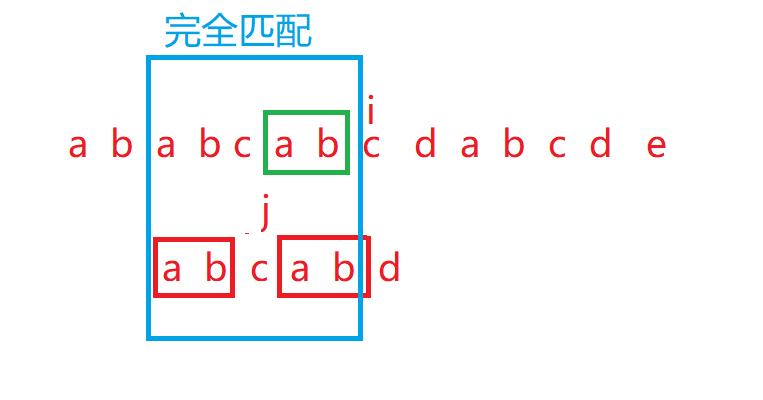
则如果 j回退到下标2的位置时，

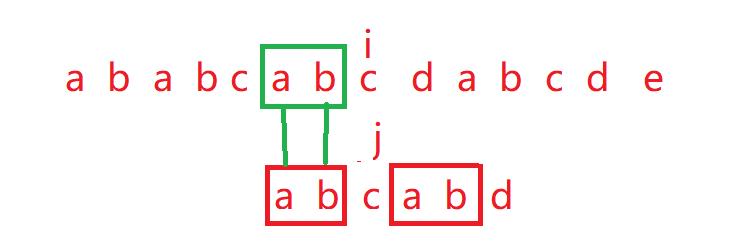
变成这样的形式，这样i就不用回退，而j只需要回退一部分即可，就又得到了子串与主串匹配的较好的基础（指不用从头依次匹配），同时也省去了相当一部分的时间去运算。直接从中间继续匹配。
在已经匹配好的字串中从头找到了一部分和主串中不匹配位置往回开始一样的部分，这样可以省去相当一部分的计算与查找时间。

当然这只是举个特例来引入KMP算法中优秀巧妙的设计。
KMP就是通过这样的设计来加快字符串匹配。

再来观察，j回退的下标，是一样的小子串的长度，因为我们必需从下标为0的位置开始找。

我当初第一次看到这种方法时，是在想如何找到这三一样的子串部分。
但是，我还忽略了一个问题，就是，如果存在这样的子串，那么，在主串与子串不匹配之前，相应大小范围的字符都是匹配的。也就是说，

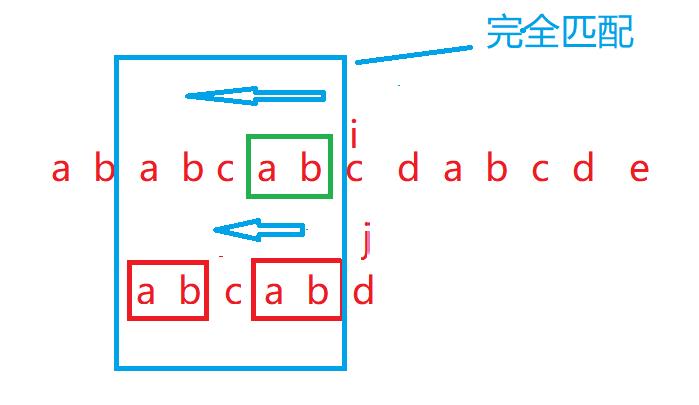
这也意味着，从不匹配处往回找，是一摸一样的，这也说明，只要在子串中找得到和从下标0开始完全一样的 小子串，那么在主串中也一定存在，则一定可以满足条件。

也就可以简化成一个伪公式

sub[0]....sub[k-1]==sub[x]...sub[i-1]
而数据长度是一样的
则；k-1+1=i-1-x+1
---x=i-k
sub[0]....sub[k-1]==sub[i-k]...sub[i-1]

找到一样的，可以继续匹配

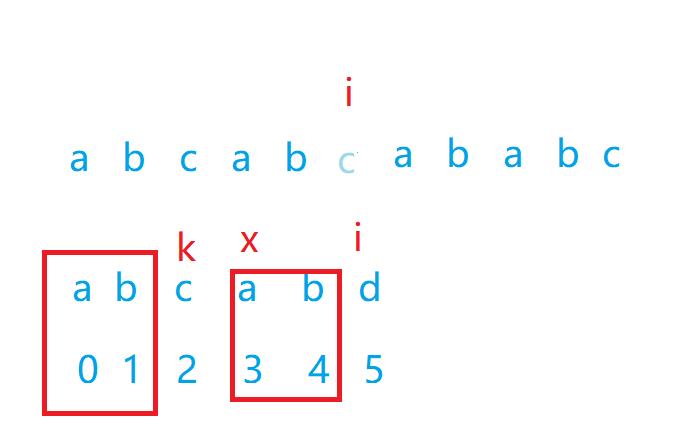
也就是说，我们根本不需要考虑主串的情况，只要在子串中寻找一样的小子串就行。而这个算法，就需要借助next数组来操作。

next数组

我们子串下标回退，不用考虑主串的情况，而子串是不会改变的，所以，下标在每个位置上，如果不匹配后，就要回退，而回退的位置是固定的，所以我们用next数组来储存下标回退的位置。而下标回退要严格遵守上述规则。
sub[0]....sub[k-1]==sub[i-k]...sub[i-1]。

拿这个来分析

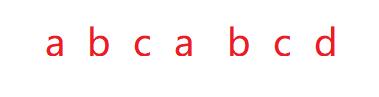
对于next数组而言，目的是储存模式串的回退下标。

先假设next[i]=k，结合上面的继续分析。

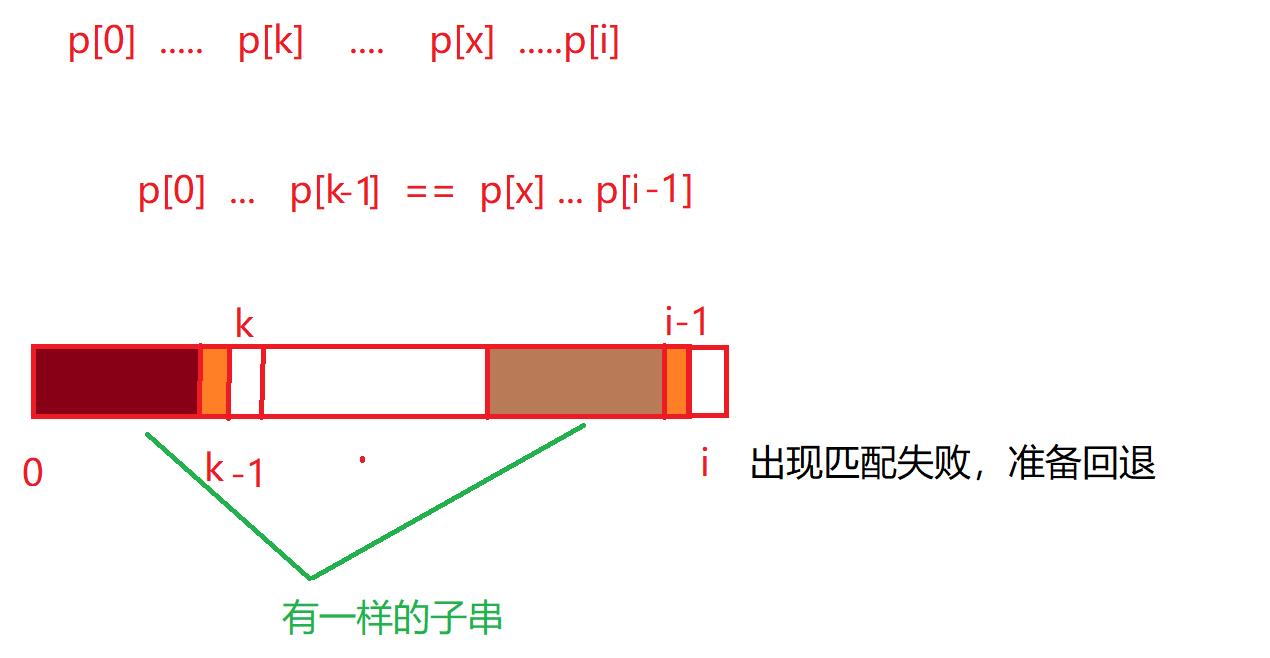
继续分析，如果p[i]==p[k]，则代表这两个前后模式串是一样的，则，如果i+1处，出现匹配失败的情况下，则i+1可以回退到k+1处，即next[i+1]=k+1。
但是如果，无法找到前后缀匹配的小子串，也就是这样的情况

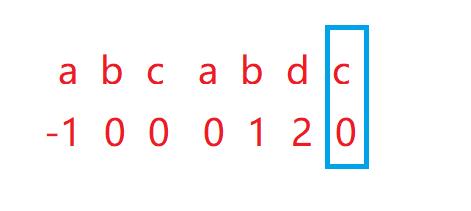
根据递推理论，我们只需要关心。这次的判断是否符合，因为，如果这次判断符合相等的条件，而前面已经按照这次的规则处理过了。不需要判断了。而这次c的匹配处出现了问题，k（前面一个元素的回退的下标）就需要再次回退，知道符合条件。

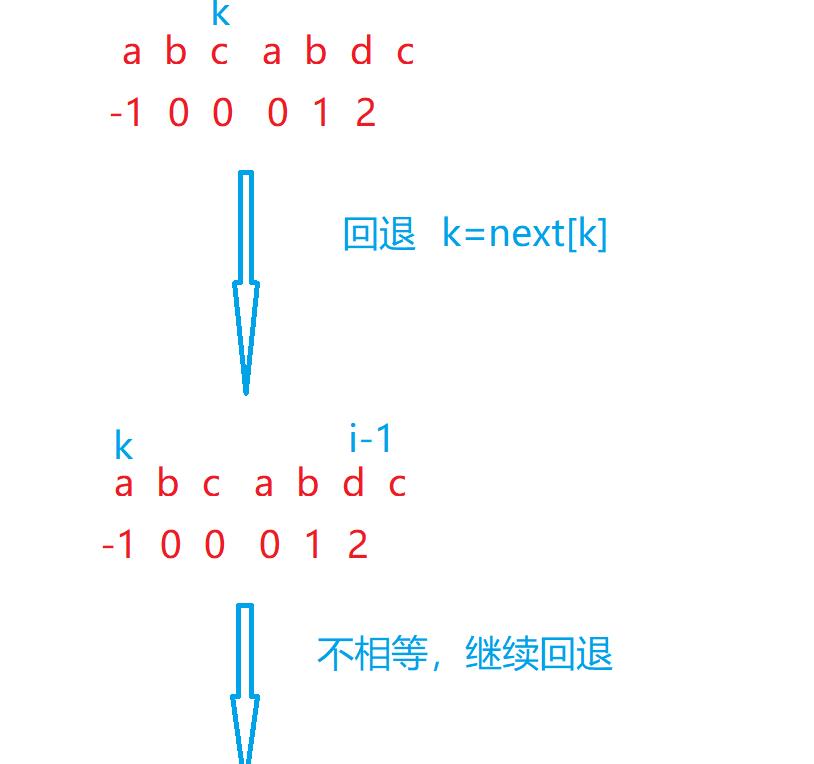
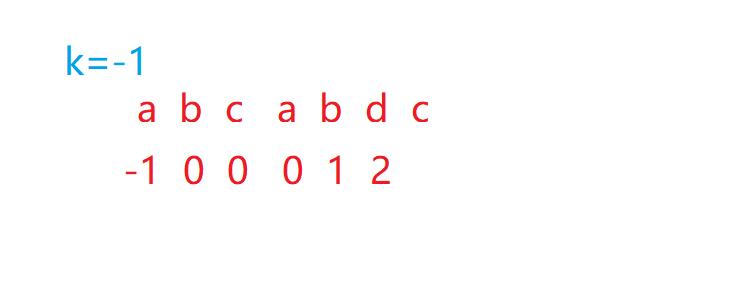
而这个k==-1的条件就意味着，i前是无法找到一样的前后缀的小字符串。也就意味着，要回退到0处。

也就是说，如果找不到前一个元素和它的回退位置的元素一样的话，就需要k一直去回退，直到找到或者，k==-1为止

代码实现next组

void GetNext(int next[],string& sub)
{
	int sublen = sub.size();
	next[0] = -1;
	int k = -1;
	for (int i = 1; i < sublen; i++)
	{	
		if ((k==-1||sub[i - 1] == sub[k]))//此时的k是上一级的k
		{
			next[i] = k + 1;
			k++; 
		}
		else
		{
			k = next[k];
		}
	}
}

要记住，如果是求i位置的回退下标，那么就需要比较 前一个位置的元素和它的回退位置的元素是否相当，如果匹配，就意味着，这两个小串可以继续向后匹配。k就回比前面要大 1。

KMP算法的实现

int KMP(string& maistr, string& substr,int pos=0)
{      ///主串           //子串           //主串开始匹配的位置
 	int i = pos; 
	int j = 0;
	int mailen = maistr.size();
	int sublen = substr.size();
	if (pos >= mailen) return -1;
	if (mailen < sublen) return -1;
	if (mailen == 0 || sublen == 0) return -1;
	int* next=new int[sublen];
	GetNext(next,substr);
	
	while (i < mailen && j < sublen)
	{
		if (j==-1 ||maistr[i] == substr[j])
		{
			i++;
			j++;
		}
		else
		{
			j = next[j];//匹配失败，开始回退
		}
	}
	delete[] next;
	return j == sublen ? i - j : -1;
}

j==-1意味着j不断回退，都找不到满足条件的小子串，就代码子串要从头开始从新比较。

时间复杂度分析

对于一个主串，一个子串而言，最坏的情况是，在最后才完成匹配，而主串的下标是不会回退的，所以走到最后的时间复杂度是O(m)。而对于next数组而言，其需要遍历子串长度的数组，也就是O(n)
所以总的是O(m+n)

总结

对于KMP算法，要利用next数组匹配回退，来减少从头匹配的次数，提高效率。但是对于子串是杂乱无序的而言，算法时间复杂度回退化严重。