JavaScript 实现二叉搜索树的操作（插入遍历最值）(ES6)

Posted 2021-09-18 YuLong~W

文章目录

• 二叉树

二叉树

树 ： 是n（n>=0)个结点的非线性表结构，n=0时称为空树。在任意一棵非空树中：

• 有且仅有一个根结点
• 当n>1时，其余结点可分为m（m>0)个互不相交的有限集T1,T2,…,Tm, 其中每一个集合本身又是一棵树，被称为根的子树
  

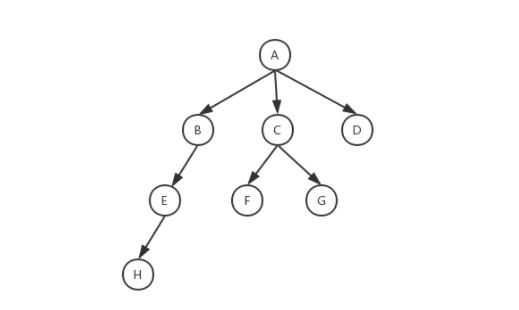
二叉树： 每个节点最多只有2个子节点的树，这两个节点分别是左子节点和右子节点

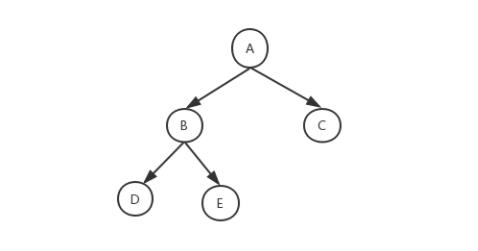
满二叉树： 有一种二叉树，叶子全部在最底层，除了叶子节点外，每个节点都有左右两个子节点

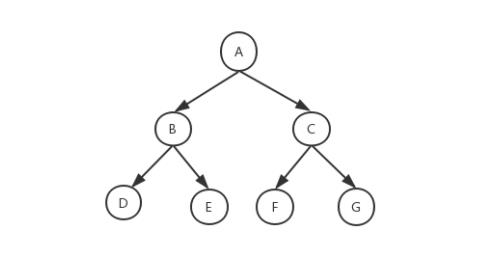
完全二叉树： 有一种二叉树，叶子节点都在最底下两层，最后一层叶节点从左到右连续，中间无缺失，并且除了最后一层，其他层的节点个数都要达到最大

二叉树的性质：

• 性质1：二叉树第i层上的结点数目最多为 2{i-1} (i≥1)。
• 性质2：深度为k的二叉树至多有2{k}-1个结点(k≥1)。
• 性质3：包含n个结点的二叉树的高度至少为log2 (n+1)。
• 性质4：在任意一棵二叉树中，若终端结点的个数为n0，度为2的结点数为n2，则n0=n2+1。

二叉树的遍历：不重复的访问二叉树中的每一个节点（递归思想）

• 前序遍历：根—左—右 即 root-left-right
• 中序遍历：左—根—右
• 后序遍历：左—右—根
• 广度优先遍历（层次遍历）：一层一层地访问，每一层的节点访问结束了再访问下一层，通过层级遍历画不出树

二叉搜索树： 是二叉树的一种，但是它只允许在左侧节点存储（比父节点）小的值， 在右侧节点存储（比父节点）大（或者等于）的值

ES6实现二叉搜索树：

class Node {
    constructor(val) {
        this.val = val;
        this.left = null;
        this.right = null;
    }
}

class binarySearchTree {
    constructor() {
        this.root = null;
        this.result_array=[];
    }

    //创建二叉搜索树 即根节点的值大于左节点的值 小于右节点的值
    insertNodeByFather(node, newNode) {
        //如果newNode<node的值
        if (newNode.val < node.val) {
            //判断左节点是否为空
            if (node.left === null) {
                node.left = newNode;
            } else { //继续递归查找下一层
                this.insertNodeByFather(node.left, newNode);
            }
        } else { //如果newNode>node的值
            if (node.right === null) {
                node.right = newNode;
            } else {
                this.insertNodeByFather(node.right, newNode);
            }
        }
    }
    insert(val) {
        //创建新的节点
        let node = new Node(val);
        if (this.root === null) { //如果没有根节点
            this.root = node;
        } else { //否则 调用insertNode方法
            this.insertNodeByFather(this.root, node);
        }
    }
    //前序遍历：根右左
    preOrder(node) {
            if (node) {
                this.result_array.push(node.val);
                this.preOrder(node.left);
                this.preOrder(node.right);
            }
    }

    //中序遍历：左根右
    inOrder(node) {
            if (node) {
                this.inOrder(node.left);
                this.result_array.push(node.val);
                this.inOrder(node.right);
            }
    }

    //后序遍历：左右根
    postOrder(node) {
        if (node) {
            this.postOrder(node.left);
            this.postOrder(node.right);
            this.result_array.push(node.val);
        }
    }
    //广度优先遍历（层次遍历）从二叉树的第一层（根结点）开始，自上至下逐层遍历；在同一层中，按照从左到右的顺序对结点逐一访问
    levelOrderTraversal(node) {
        if (!node) {
            throw new Error('Empty Tree');
        }
        let que = [];
        que.push(node)
        while (que.length !== 0) {
            node = que.shift()
            this.result_array.push(node.val)
            if (node.left) que.push(node.left)
            if (node.right) que.push(node.right)
        }
    }
    //清除存放的树节点的值
    init(){
        this.result_array=[];
    }

    //搜索最小值
    minNode(node){
        if (!node) return null;
        while (node.left){
            node=node.left;
        }
        return node.val;
    }

    //搜索最大值
    maxNode(node){
        if (!node) return null;
        while (node.right){
            node=node.right;
        }
        return node.val;
    }
}

检测代码：

let tree = new binarySearchTree();
let arr = [11,7,15,5,9,4,6,8,10];
arr.forEach((a) => {
    tree.insert(a);
});

let pre_arr = []; //存放前序遍历序列
let in_arr = []; //存放中序遍历序列
let post_arr = []; //存放后序遍历序列
let level_arr = []; //存放层次遍历序列

tree.preOrder(tree.root);
pre_arr=tree.result_array;
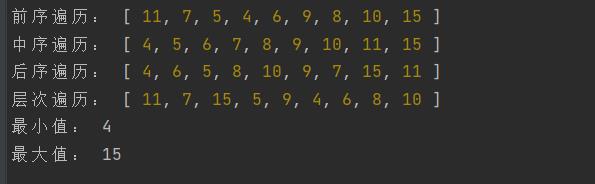
console.log('前序遍历：',pre_arr);

tree.init();//清空数组里的值
tree.inOrder(tree.root);
in_arr=tree.result_array;
console.log('中序遍历：',in_arr);

tree.init();
tree.postOrder(tree.root);
post_arr=tree.result_array;
console.log('后序遍历：',post_arr);

tree.init();
tree.levelOrderTraversal(tree.root);
level_arr=tree.result_array;
console.log('层次遍历：',level_arr);

console.log('最小值：',tree.minNode(tree.root));
console.log('最大值：',tree.maxNode(tree.root));

输出结果：

案例：输入二叉树的前序和中序遍历的数组结果，确定二叉树结构

 class binaryTree {
    constructor(v, l, r) {
        this.val = v;
        this.left = l;
        this.right = r
    }
}

/**
 * 输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。
 * 假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
 * 例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历列{4,7,2,1,5,3,8,6}，
 * 则重建二叉树并返回。
 * 
 *   输入：  前序：[1,2,3,4,5,6,7],中序：[3,2,4,1,6,5,7]   
     输出：    树的结构
 */

function reConstructBinaryTree(pre, next) {
    // 递归出口
    if (pre.length == 0 || next.length == 0 || pre.length != next.length) {
        return null;
    }
    // 拿到根结点
    let root = new binaryTree(pre[0]);
    // 找的根结点在中序遍历中的位置
    let i = 0;
    while (next[i] != root.val) {
        i++;
    }
    //确定左子树前序遍历长度
    let preLeft = new Array(i);
    //确定左子树中序遍历长度
    let inLeft = new Array(i);

    //确定右子树前序遍历长度
    let preRight = new Array(next.length - i - 1);
    //确定右子树中序遍历长度
    let inRight = new Array(next.length - i - 1);

    // 遍历依次拿到左右子树  前中序遍历的值
    for (let j = 0; j < next.length; j++) {
        if (j < i) {
            preLeft[j] = pre[j + 1];  //从j+1开始
            inLeft[j] = next[j];      //从j开始
        } else if (j > i) {
            preRight[j - i - 1] = pre[j];
            inRight[j - i - 1] = next[j];
        }
    }
    // 递归
    root.left = reConstructBinaryTree(preLeft, inLeft);
    root.right = reConstructBinaryTree(preRight, inRight);
    return root;
}

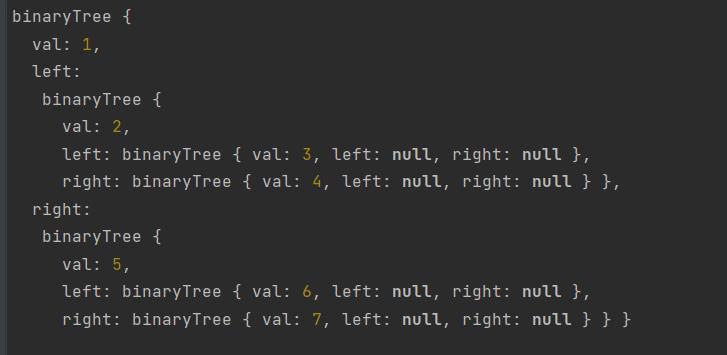
测试： 已知前序和中序确定树的结构

let pre = [1, 2, 3, 4, 5, 6, 7];
let next = [3, 2, 4, 1, 6, 5, 7];
let root = reConstructBinaryTree(pre, next);
console.log(root);

二叉树的结构：