数学建模 非线性规划原理的应用与编程实现
Posted DQ_CODING
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数学建模 非线性规划原理的应用与编程实现相关的知识,希望对你有一定的参考价值。
非线性规划模型NP
包含非线性函数:不是直线而是曲线、曲面、或不确定的属性,叫非线性。
如:x^2
线性函数:一次函数,ax+b

列1-投资决策问题

解答:
设置决策变量:
1)投资某个项目达到收益最高,使用比值法(更直观)
收益/投资花费

取值范围
1)*非线性规划中常用
限制xi=0或1(在编程中) xi(1-xi)=0

数学模型:

如果增设一个风险(不确定),此时需要:投资收益-风险-投资,但在此题中没有风险,所以直接用收益/投资就行
非线性规划的数学模型

matlab中非线性规划的数学模型
s.t内前两个是线性规划函数,后两个是非线性规划函数
c(x)<=0 非线性规划的不等式
ceq(x)=0非线性规划的等式
lb上界 ub下界

matlab中的命令:
[x,fval]=fmincon()

普通的非线性规划例子

matlab编写过程

二次规划
1)约束条件全部是线性函数ax+b
2)实对称矩阵:矩阵元素沿着对角线是对称的
如:
1 0 0
0 1 0
0 0 1
3)目标函数中有二次函数也有一次函数f^t x
4)标准形式中是1/2x^2,所以在带值进入函数时
x^2的系数*2
5)x^T是转置矩阵

matlab中求解二次规划的命令:
x0:非线性函数的初值

二次规划例子
系数变为原来的两倍:
2x1^2–>4
-4x1x2–>-8
+4x2^2–>8
-8是x1x2,所以使用时是-4 -4

应用实例-供应与选址
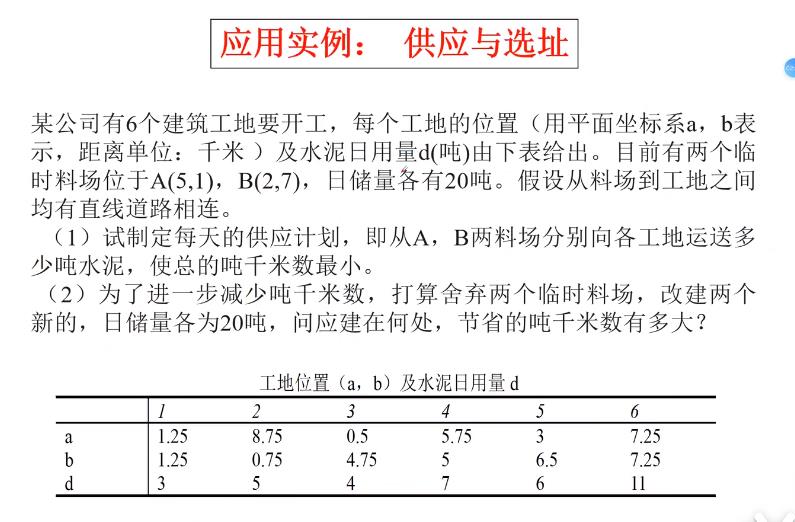
解答:
建立模型:
1)吨千米数:吨千米数
2)两个料场运输到6个工地,共有26=12个决策变量
3)新建立两个料场,现在每个料场的坐标不知道,就有12+4=16个未知数/决策变量,这只是多了4个变量,因此可以1,2问一起写
4)题目中写明了分别向工地运输多少吨水泥,所以直接设置每个料场向工地的运输量为xij
5)xij的和即料场向工地运输的量要满足每个工地的需求di
6)xij的和<=ej
x11+x21+x31+x41+x51+x61<=e1
x21+x22+x32+x42+x52+x62<=e2
从料场1向所有工地运输的量小于其存储量
从料场2向所有工地运输的量小于其存储量

第一问:
使用临时料场的情况:

matlab代码:


计算结果:
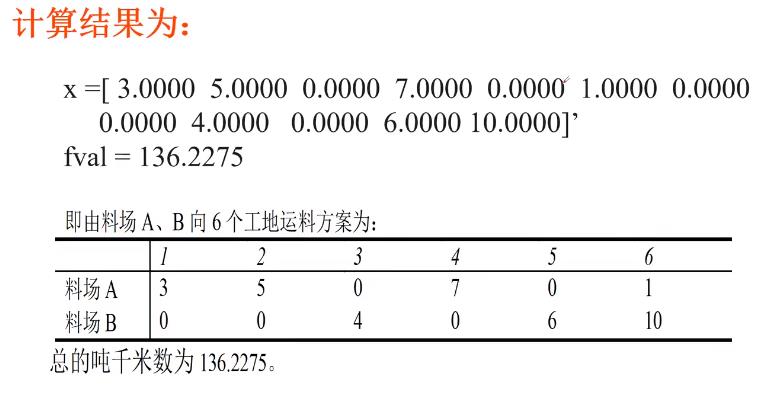
第二问:
改建两个新料场的情况:

matlab代码:

第一个程序:

第二个程序:


计算结果:
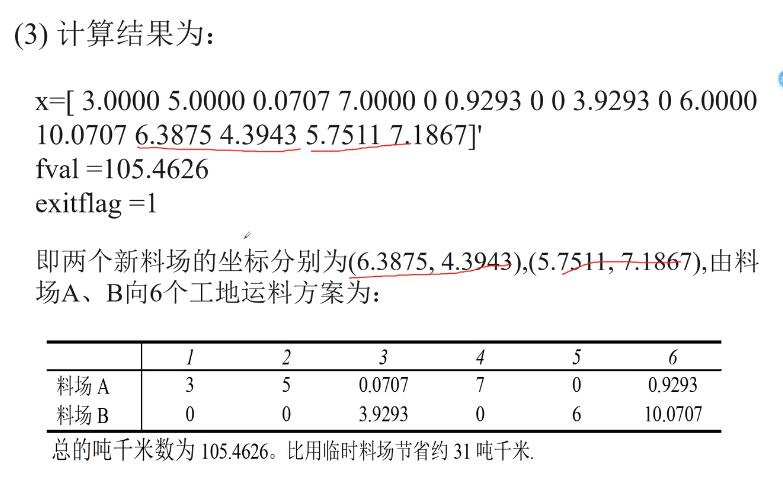
如果取初值为上面运算的结果:
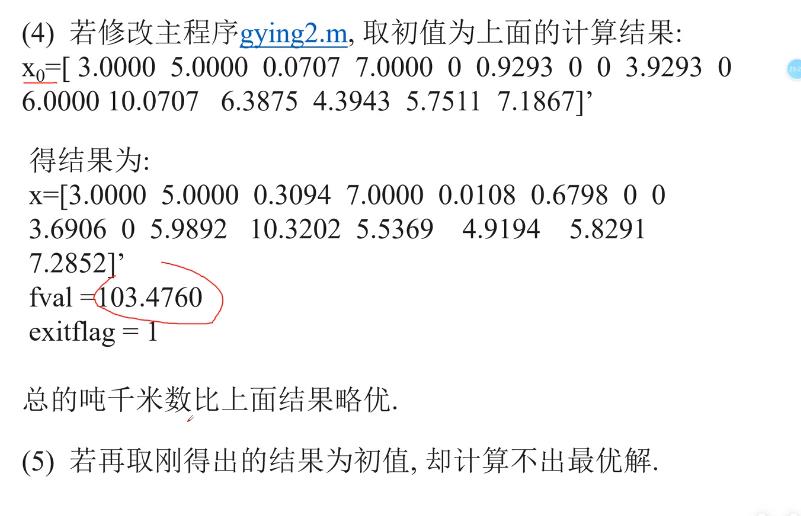
以上是关于数学建模 非线性规划原理的应用与编程实现的主要内容,如果未能解决你的问题,请参考以下文章