79. 单词搜索

Posted 2021-09-17 炫云云

79. 单词搜索

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

例如，在下面的 3×4 的矩阵中包含单词 “ABCCED”（单词中的字母已标出）。

示例 1：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

示例 2：

输入：board = [["a","b"],["c","d"]], word = "abcd"
输出：false

提示：

1 <= board.length <= 200
1 <= board[i].length <= 200
board 和 word 仅由大小写英文字母组成

回溯

思路与算法

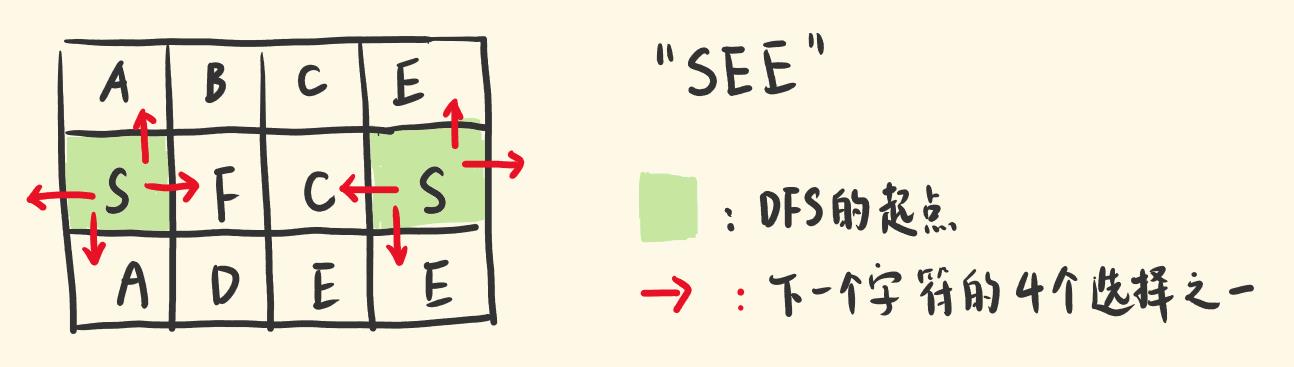
• 以"SEE"为例，首先要选对起点：遍历一遍矩阵，找到起点S。
• 起点可能不止一个，基于其中一个S，看看能否找出剩下的"EE"路径。
• 下一个字符E有四个可选点：当前点的上、下、左、右。
• 逐个尝试每一种选择。基于当前选择，为下一个字符选点，又有四种选择，继续探索。
• 每到一个点做的事情是一样的。DFS 往下选点，构建路径。
• 当发现某个选择不对，不用继续选下去了，结束当前递归，考察别的选择。

设函数 $\text{check}(i,j,index)$ 表示判断以网格的 $(i,j)$ 位置出发，能否搜索到单词 $\text{word}[index..]$ ，其中 $\text{word}[index..]$ 表示字符串 $\text{word}$ 从第 $index$ 个字符开始的后缀子串。如果能搜索到，则返回 $\text{true}$ ，反之返回 $\text{false}$ 。函数 $\text{check}(i,j,index)$ 的执行步骤如下：

• 如果 $\text{board}[i][j]\ne word[index]$ ，当前字符不匹配，直接返回 $\text{false}$ 。
• 如果当前已经访问到字符串的末尾，且对应字符依然匹配，此时直接返回 $\text{true}$​ 。
• 否则，遍历当前位置的所有相邻位置。如果从某个相邻位置出发，能够搜索到子串 $\text{word}[index+1..]$​ ，则返回 $\text{true}$​ ，否则返回 $\text{false}$​ 。

这样，我们对每一个位置 $(i,j)$ 都调用函数 $\text{check}(i,j,0)$ 进行检查：只要有一处返回 $\text{true}$ ，就说明网格中能够找到相应的单词，否则说明不能找到。

为了防止重复遍历相同的位置，需要额外维护一个与 $\text{board}$ 等大的 $\text{visited}$ 数组，用于标识每个位置是否被访问过。每次遍历相邻位置时，需要跳过已经被访问的位置。

class Solution(object):
    def exist(self, board, word):
        """
        :type board: List[List[str]]
        :type word: str
        :rtype: bool
        """
        directions = [(0, 1), (0, -1), (1, 0), (-1, 0)] #(i,j)的移动
        def check(i,j,index):
            if board[i][j] != word[index]: 
                return False
            elif index == lenw - 1: # 最后一个字母了
                return True
            visited.add((i, j)) #记录一下当前点被访问
            result = False
            for di, dj in directions:
                newi, newj = i + di, j + dj
                # 在矩阵范围内且没有被使用过,不遍历相同位置
                if 0<= newi < h and 0<=newj < w and (newi, newj) not in visited :
                    if check(newi,newj,index+1):
                        result =True
                        break
            visited.remove((i, j))
            return result

        h, w = len(board), len(board[0])
        lenw = len(word)
        # 判断数目
        board_count = Counter(board[i][j] for i in range(h) for j in range(w))
        word_count = Counter(word)
        for key in word_count.keys():
            if word_count[key] > board_count[key]:
                return False

        visited = set()
        for i in range(h):
            for j in range(w):
                if check(i, j, 0):# 如果返回的是true,则直接返回，反之则继续
                    return True
        return False

深度优先搜索（DFS）+ 剪枝

本问题是典型的矩阵搜索问题，可使用 深度优先搜索（DFS）+ 剪枝 解决。

• 深度优先搜索： DFS 通过递归，先朝一个方向搜到底，再回溯至上个节点，沿另一个方向搜索，以此类推。
• 剪枝： 在搜索中，遇到 这条路不可能和目标字符串匹配成功的情况（例如：此矩阵元素和目标字符不同、此元素已被访问），则应立即返回，称之为可行性剪枝 。

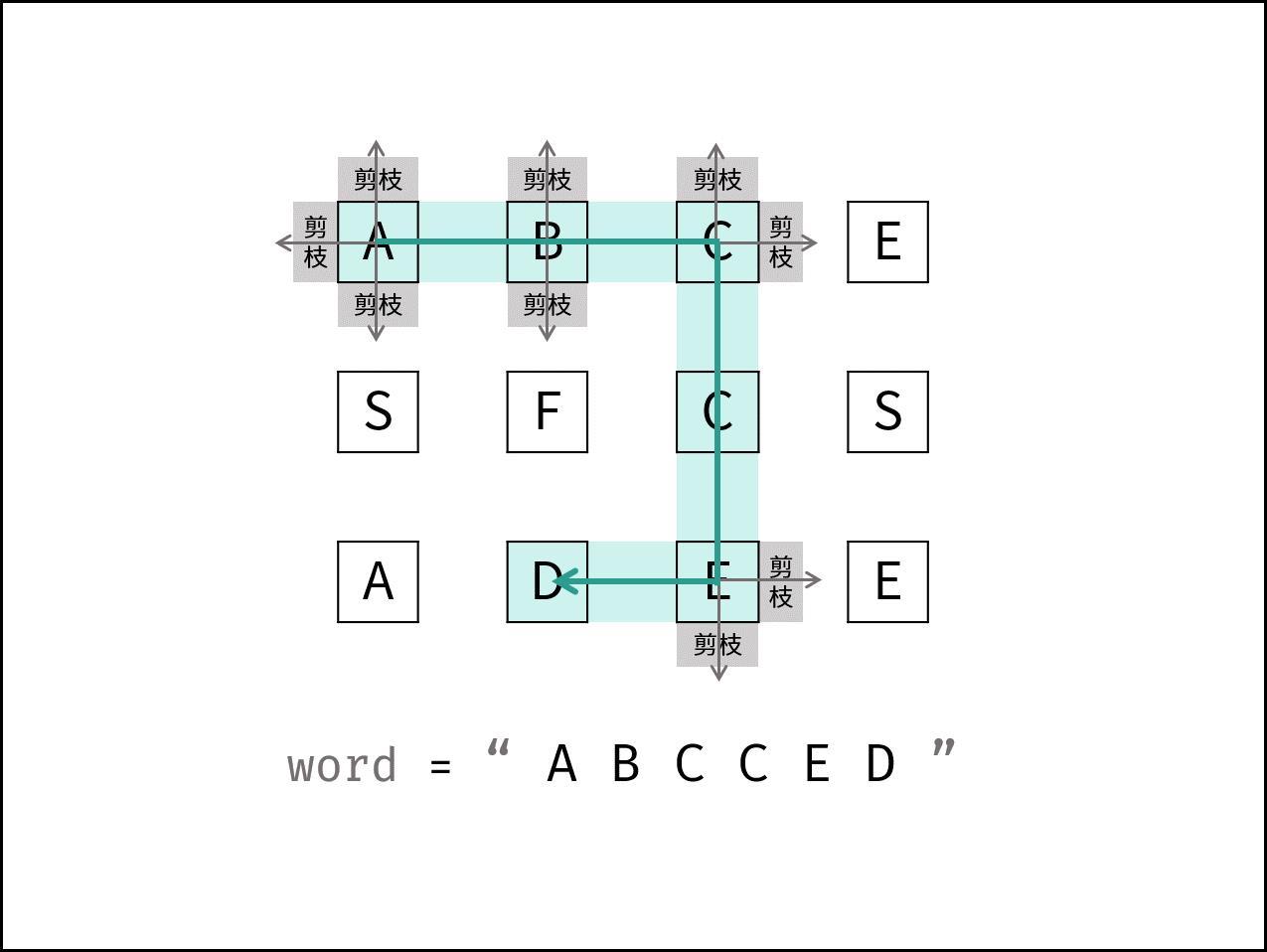
DFS 解析：

• 递归参数： 当前元素在矩阵 board 中的行列索引 $i$ 和 $j$ ，当前目标字符在 word 中的索引 $index$ 。

• 终止条件：

• • 返回 false ： (1) 行或列索引越界 或 (2) 当前矩阵元素与目标字符不同 或 (3) 当前矩阵元素已访问过 （ (3) 可合并至 (2) ） 。
• • 返回 true ： $index==len(word)-1$ ，即字符串 word 已全部匹配。

• 递推工作：

• • 标记当前矩阵元素： 将 board[i][j] 修改为 空字符 '' ，代表此元素已访问过，防止之后搜索时重复访问。
• • 搜索下一单元格： 朝当前元素的 上、下、左、右 四个方向开启下层递归，使用 或 连接 （代表只需找到一条可行路径就直接返回，不再做后续 DFS ），并记录结果至 res 。
• • 还原当前矩阵元素： 将 board[i][j] 元素还原至初始值，即 word[index] 。

• 返回值： 返回布尔量 res ，代表是否搜索到目标字符串。

使用空字符做标记是为了防止标记字符与矩阵原有字符重复。当存在重复时，此算法会将矩阵原有字符认作标记字符，从而出现错误。

复杂度分析：

$M,N$ 分别为矩阵行列大小, $K$​ 为字符串 word 长度。

• 时间复杂度 $O\left(3^{K}MN\right)$ : 最差情况下，需要遍历矩阵中长度为 $K$ 字符串的所有方案, 时间复 杂度为 $O\left(3^K\right)$; 矩阵中共有 $MN$ 个起点， 时间复杂度为 $O(MN)$ 。
• • 方案数计算：设字符串长度为 $K$ ，搜索中每个字符有上、下、左、右四个方向可以选择, 舍弃回头（上个字符) 的方向，剩下 3 种选择，因此方案数的复杂度为 $O\left(3^K\right)$ 。
• 空间复杂度 $O(K)$ : 搜索过程中的递归深度不超过 $K$ ， 因此系统因函数调用累计使用的栈空 间占用 $O(K)$ (因为函数返回后，系统调用的栈空间会释放) 。最坏情况下 $K=MN$, 递归 深度为 $MN$, 此时系统栈使用 $O(MN)$ 的额外空间。

class Solution(object):
    def exist(self, board, word):
        """
        :type board: List[List[str]]
        :type word: str
        :rtype: bool
        """
        def dfs(i,j,index):
            if not 0 <= i < h or not 0 <= j < w or board[i][j] != word[index]: 
                return False
            elif index == len(word) - 1:# 最后一个字母了
                return True
            board[i][j] = ''
            res = dfs(i + 1, j, index + 1) or dfs(i - 1, j, index + 1) or dfs(i, j + 1, index + 1) or dfs(i, j - 1, index + 1)
            board[i][j] = word[index]
            return res

        h, w = len(board), len(board[0])
        # 判断数目
        board_count = Counter(board[i][j] for i in range(h) for j in range(w))
        word_count = Counter(word)
        for key in word_count.keys():
            if word_count[key] > board_count[key]:
                return False

        for i in range(h):
            for j in range(w):
                if dfs(i, j, 0): return True
        return False

参考

Krahets - 力扣（LeetCode） (leetcode-cn.com)