123. 买卖股票的最佳时机 III

Posted 2021-09-17 炫云云

123. 买卖股票的最佳时机 III

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。

**注意：**你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

输入：prices = [3,3,5,0,0,3,1,4]
输出：6

解释：在第 4 天（股票价格 = 0）的时候买入，在第 6 天（股票价格 = 3）的时候卖出，
		这笔交易所能获得利润 = 3-0 = 3 。
     随后，在第 7 天（股票价格 = 1）的时候买入，
     在第 8 天 （股票价格 = 4）的时候卖出，这笔交易所能获得利润 = 4-1 = 3 。

动态规划

状态定义：dp[i][j][k] 表示在 [0, i] 区间里（状态具有前缀性质），交易进行了 j 次，并且状态为 k 时我们拥有的现金数。其中 j 和 k 的含义如下：

• j = 0 表示没有交易发生；
• j = 1 表示此时已经发生了 1 次买入股票的行为；
• j = 2 表示此时已经发生了 2 次买入股票的行为。

即我们 人为规定 记录一次交易产生是在 买入股票 的时候。

• k = 0 表示当前不持股；
• k = 1 表示当前持股。

推导状态转移方程：

「状态转移方程」可以用下面的图表示，它的特点是：状态要么什么都不做，要么向后面走，即：状态不能回退。

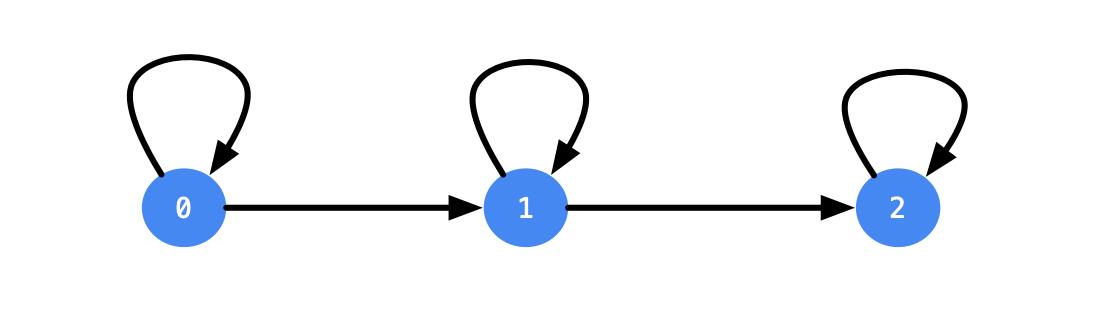
具体表示式请见代码注释。

思考初始化：

下标为 0 这一天，交易次数为 0 、1 、2 并且状态为 0 和 1 的初值应该如下设置：

• dp[0][0][0] = 0：这是显然的；
• dp[0][0][1]：表示一次交易都没有发生，但是持股，这是不可能的
• dp[0][1][0] = 0：表示发生了 1 次交易，但是不持股，这是不可能的。
• dp[0][1][1] = -prices[0]：表示发生了一次交易，并且持股，所以我们持有的现金数就是当天股价的相反数；
• dp[0][2][0] = 0：表示发生了 2 次交易，但是不持股，这是不可能的。虽然没有意义，但是设置成 0 不会影响最优值；
• dp[0][2][1] = 负无穷：表示发生了 2 次交易，并且持股，这是不可能的。注意：虽然没有意义，但是不能设置成 0，

最后一天不持股的状态都可能成为最大利润。

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        if not prices:
            return 0
        n = len(prices)
        if n<2:
            return 0
        # 定义三维数组：第i天、交易了多少次、当前的买卖状态
        # 第 2 维的 0 没有意义，1 表示交易进行了 1 次，2 表示交易进行了 2 次
        # 为了使得第 2 维的数值 1 和 2 有意义，这里将第 2 维的长度设置为 3
        dp = [[[0  for _ in range(2)] for _ in range(3)] for _ in range(n)]

        # 理解如下初始化
        # 第 3 维规定了必须持股，因此是 -prices[0]
        dp[0][1][1] = -prices[0];
        #还没发生的交易，持股的时候应该初始化为负无穷
        dp[0][2][1] =-float('inf')
        for i in range(1,n):
            dp[i][1][1] = max(dp[i - 1][1][1], -prices[i] )#发生了一次交易，并且持股
            dp[i][1][0] = max( dp[i - 1][1][0] , dp[i - 1][1][1] +prices[i]  )#发生了一次交易，不持股
            
            dp[i][2][1] =max(dp[i-1][2][1], dp[i][1][0] - prices[i])  #发生了2次交易，并且持股
            dp[i][2][0] = max(dp[i-1][2][0], dp[i-1][2][1] +  prices[i] )#发生了2次交易，不持股

        return max(dp[-1][1][0],dp[-1][2][0])

空间优化

由于今天只参考了昨天的状态，所以直接去掉第一维不会影响状态转移的正确性）

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        if not prices:
            return 0
        n = len(prices)
        if n<2:
            return 0
        dp = [[0  for _ in range(2)] for _ in range(3)] 
        # 第 2 维规定了必须持股，因此是 -prices[0]
        dp[1][1] = -prices[0];
        #还没发生的交易，持股的时候应该初始化为负无穷
        dp[2][1] =-float('inf')
        for i in range(1,n):
            dp[1][1] = max(dp[1][1], -prices[i])
            dp[1][0] =  max(dp[1][0], dp[1][1]+prices[i])

            dp[2][1] = max(dp[2][1], dp[1][0]-prices[i])
            dp[2][0] =  max(dp[2][0], dp[2][1]+prices[i])
        return max( dp[2][0] ,dp[1][0]  )

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        n = len(prices)
        buy1 = buy2 = -prices[0] #买进
        sell1 = sell2 = 0  # 卖出
        for i in range(1, n):
            buy1 = max(buy1, -prices[i])
            sell1 = max(sell1, buy1 + prices[i])
            buy2 = max(buy2, sell1 - prices[i])
            sell2 = max(sell2, buy2 + prices[i])
        return sell2

参考

Krahets - 力扣（LeetCode） (leetcode-cn.com)