算法笔记：并查集

Posted 2021-09-17 UQI-LIUWJ

1 并查集介绍

        并查集主要用于解决一些元素分组的问题。它管理一系列不相交的集合，并支持两种操作：

• 合并（Union）：把两个不相交的集合合并为一个集合。
• 查询（Find）：查询两个元素是否在同一个集合中。

2 用比武的方式解释并查集

        并查集的重要思想在于，用集合中的一个元素代表集合。我们不妨把集合比喻成帮派，而代表元素则是帮主。

        接下来我们利用这个比喻，看看并查集是如何运作的。

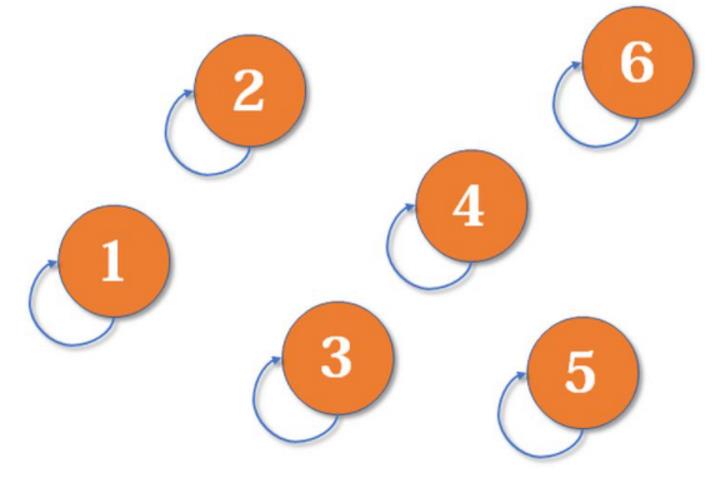
        最开始，所有大侠各自为战。他们各自的帮主自然就是自己。（对于只有一个元素的集合，代表元素自然是唯一的那个元素）

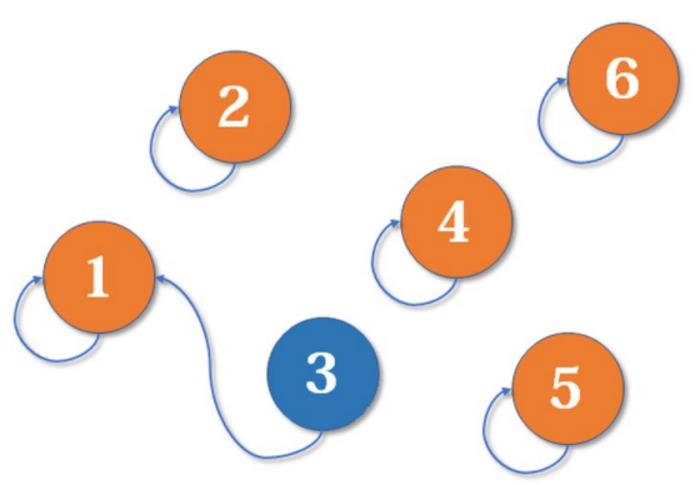
        现在1号和3号比武，假设1号赢了（这里具体谁赢暂时不重要），那么3号就认1号作帮主（合并1号和3号所在的集合，1号为代表元素）。       

 

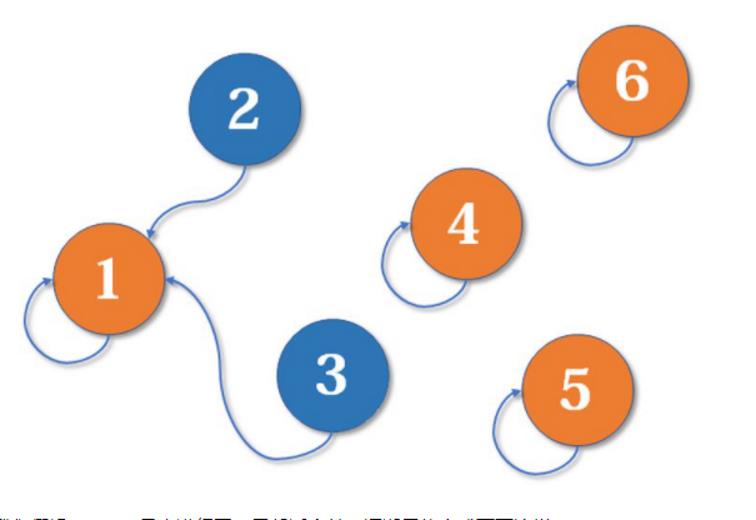
        现在2号想和3号比武（合并3号和2号所在的集合），但3号表示，别跟我打，让我帮主来收拾你（合并代表元素）。不妨设这次又是1号赢了，那么2号也认1号做帮主。

 

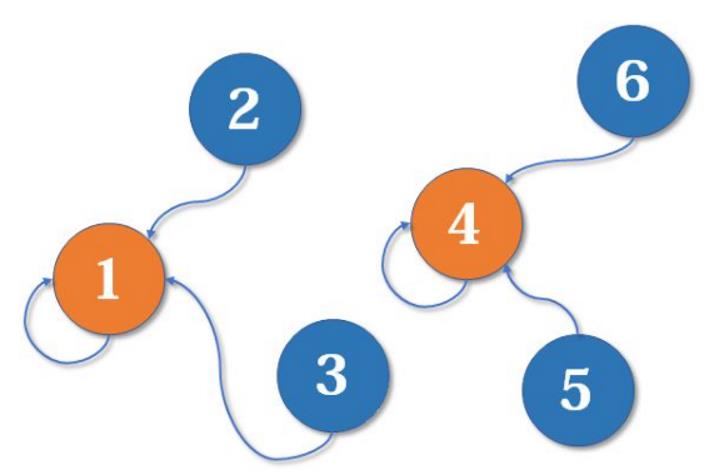
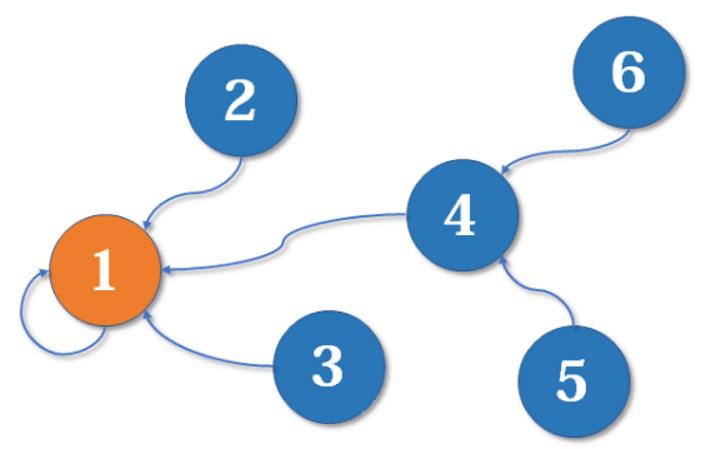
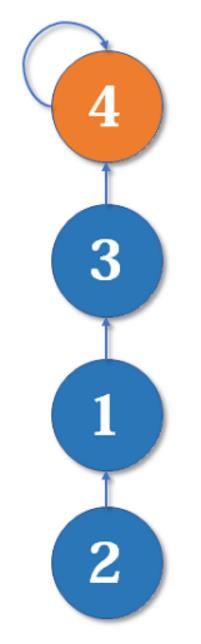
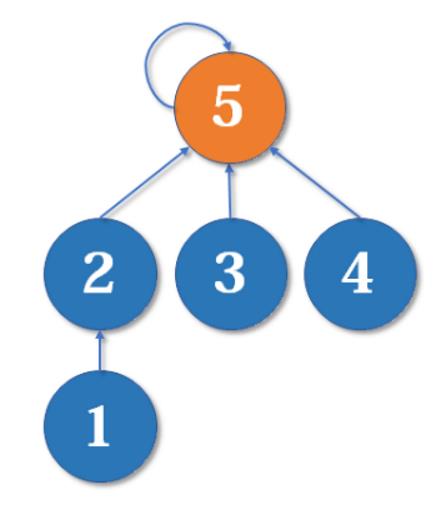
 现在我们假设4、5、6号也进行了一番帮派合并，江湖局势变成下面这样：

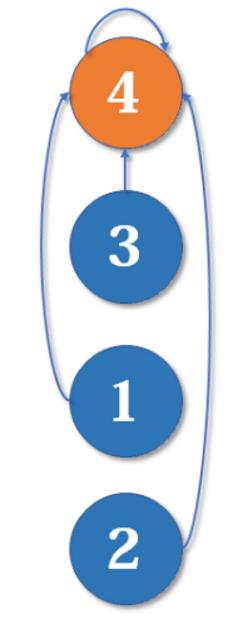
 现在假设2号想与6号比，跟刚刚说的一样，喊帮主1号和4号出来打一架【小弟约架，帮主出面】。1号胜利后，4号认1号为帮主，当然他的手下也都是跟着投降了。 

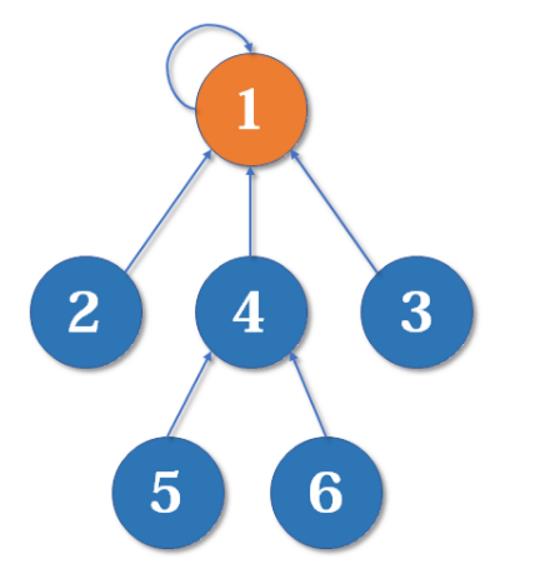
        不难发现，这是一个树状的结构，要寻找集合的代表元素，只需要一层一层往上访问父节点（图中箭头所指的圆），直达树的根节点（图中橙色的圆）即可。根节点的父节点是它自己。我们可以直接把它画成一棵树：

 3 原始并查集代码部分

假设我们有5个点

3.1 初始化

naive_union_find=[0]
for i in range(1,5+1):
    naive_union_find.append(i)
naive_union_find
'''
[0, 1, 2, 3, 4, 5]
'''

        假如有编号为1, 2, 3, 4, 5的5个元素，我们用一个数组naive_union_find来存储每个元素的父节点（因为每个元素有且只有一个父节点，所以这是可行的）。

        一开始，我们先将它们的父节点设为自己。

        假设有n个点，那么初始化操作的时间复杂度是O(n)

3.2 查询

        查找一个节点的根节点（也就是这个节点属于哪个“帮派”）

def find(x):
    if(naive_union_find[x]=x):
        return x
    else:
        return find(naive_union_find[x])

        我们用递归的写法实现对代表元素的查询：一层一层访问父节点，直至根节点（根节点的标志就是父节点是本身）。

        要判断两个元素是否属于同一个集合，只需要看它们的根节点是否相同即可。

        假设有n个点，那么合并操作的时间复杂度是O(树的深度)【从叶子节点到根节点层层遍历上去】

       定理：在并查集中， 假设有n个点，那么树的最大深度为O(logn)

        证明：

1. 当包含u的集合被合并了之后，整体并查集树的深度最多增加1（在5.2节我们会知道，只有合并的两棵并查集树深度一样的时候，整体并查集树的深度才会增加1）
2. 因为我们都是深度小的树往深度大的数合并，所以如果深度增加的话，整体并查集数的节点数量至少翻倍
3. 节点的数量是n，所以层数最多O(logn)

         所以，此时合并操作的时间复杂度是O(logn)

3.3 合并

def merge(i,j):
    naive_union_find[find(i)]=find(j)

        合并操作也是很简单的，先找到两个集合的代表元素，然后将前者的父节点设为后者即可。        

        当然也可以将后者的父节点设为前者，这里暂时不重要。之后会给出一个更合理的比较方法。 

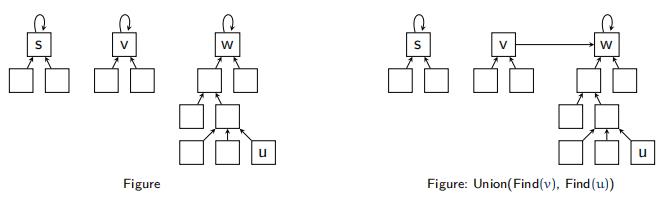
         假设有n个点，那么合并操作的时间复杂度是O(1)

 4 路径压缩

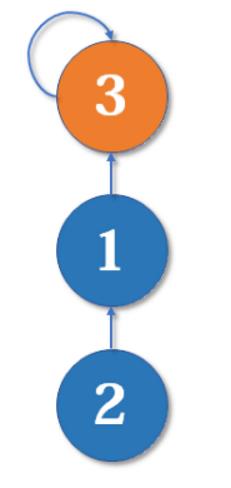
最简单的并查集效率是比较低的。例如，来看下面这个场景：

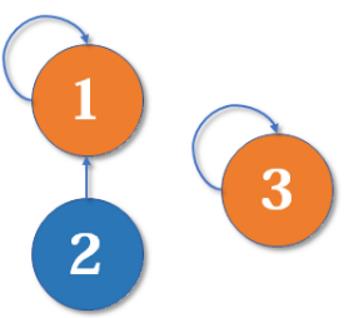
现在我们要merge(2,3)，于是从2找到1，naive_union_find[1]=3，于是变成了这样：

 

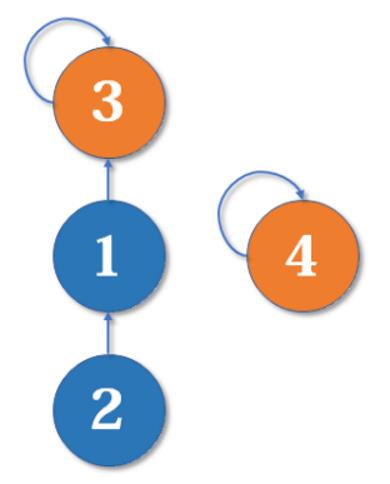
 然后我们又找来一个元素4，并需要执行merge(2,4)：

 

从2找到1，再找到3，然后naive_union_find[3]=4，于是变成了这样：

 

 这样可能会形成一条长长的链，随着链越来越长，我们想要从底部找到根节点会变得越来越难。

 怎么解决呢？我们可以使用路径压缩的方法。既然我们只关心一个元素对应的根节点，那我们希望每个元素到根节点的路径尽可能短，最好只需要一步，像这样：

 其实这说来也很好实现。只要我们在查询的过程中，把沿途的每个节点的父节点都设为根节点即可。下一次再查询时，我们就可以省很多事。这用递归的写法很容易实现：

def find(x):
    if(naive_union_find[x]=x):
        return x
    else:
        #return find(naive_union_find[x]) 原来的查询

        naive_union_find[x]=find(naive_union_find[x])
        #将目前节点的父节点直接设置为根节点

        return(naive_union_find[x])
        #返回当前节点的父节点，也就是根节点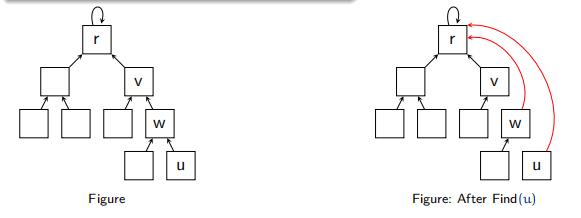

         路径压缩优化后，并查集的时间复杂度已经比较低了，绝大多数不相交集合的合并查询问题都能够解决。然而，对于某些时间卡得很紧的题目，我们还可以进一步优化。

        有些人可能有一个误解，以为路径压缩优化后，并查集始终都是一个菊花图（只有两层的树的俗称）。但其实，由于路径压缩只在查询时进行，也只压缩一条路径，所以并查集最终的结构仍然可能是比较复杂的。

4.1 路径压缩的效率提升

        直接看结论吧：使用路径压缩之后，Find操作的平均时长为O(α(n))，其中α(n)是阿克曼函数（Ackermann function ）A(n,n)的倒数

 4.1.2 阿克曼函数

        阿克曼函数的定义如下：

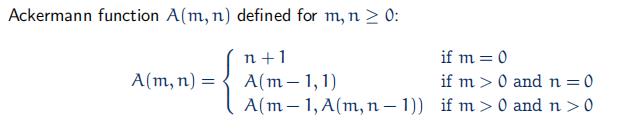
这是一个增长速度很快的函数

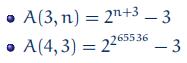
        而使用路径压缩之后，Find操作的平均时间复杂度是O(α(n))，，其中α(n)是阿克曼函数（Ackermann function ）A(n,n)的倒数。所以是一个很小的数。（经验结论，对于一般的数据集来说，α(n)≤5）

5 按秩合并

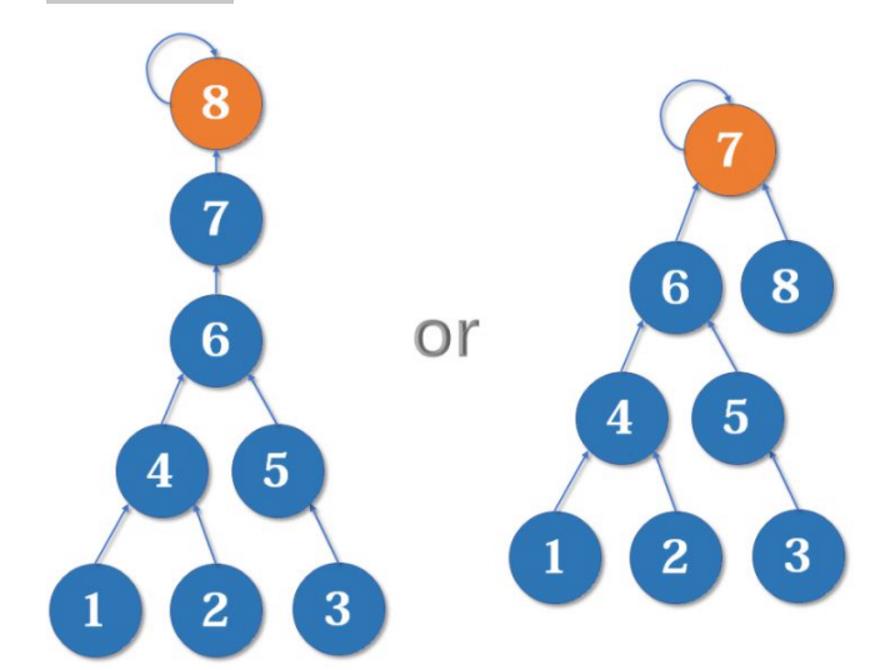
现在我们有一棵较复杂的树需要与一个单元素的集合合并

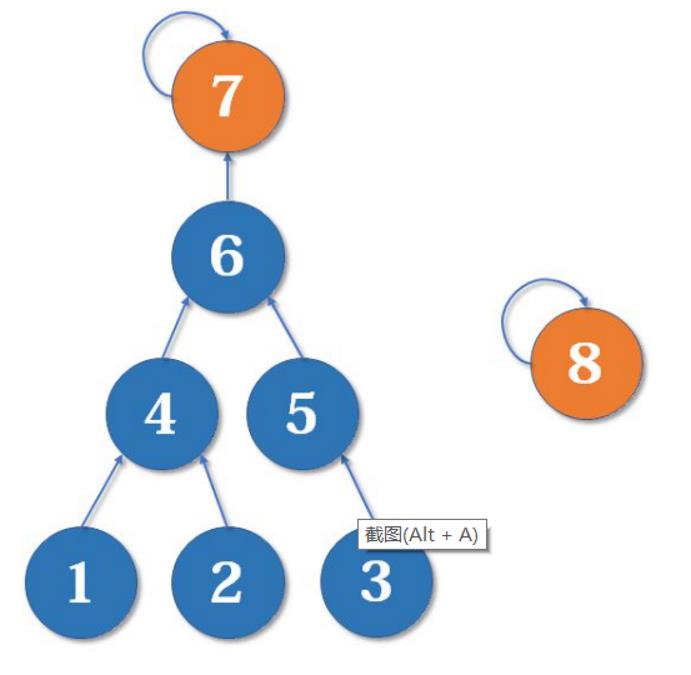
        假如这时我们要merge(7,8)，如果我们可以选择的话，是把7的父节点设为8好，还是把8的父节点设为7好呢？

        

        当然是后者。因为如果把7的父节点设为8，会使树的深度（树中最长链的长度）加深，原来的树中每个元素到根节点的距离都变长了，之后我们寻找根节点的路径也就会相应变长。虽然我们有路径压缩，但路径压缩也是会消耗时间的。而把8的父节点设为7，则不会有这个问题，因为它没有影响到不相关的节点。 

        这启发我们：我们应该把简单的树往复杂的树上合并，而不是相反。因为这样合并后，到根节点距离变长的节点个数比较少。

        我们用一个数组rank[]记录每个根节点对应的树的深度（如果不是根节点，其rank相当于以它作为根节点的子树的深度）。

        一开始，把所有元素的rank（秩）设为1。合并时比较两个根节点，把rank较小者往较大者上合并。

  5.1 初始化（按秩合并）

naive_union_find=[0]
#记录每个节点对应的父节点
rank_union_find=[0]
#记录每个节点的秩
for i in range(1,5+1):
    naive_union_find.append(i)
    rank_union_find.append(1)

5.2 合并（按秩合并）

def merge(i,j):
    i=find(i)
    j=find(j)

    if(rank_union_find[i]>rank_union_find[j]):
        naive_union_find[j]=i
    else:
        naive_union_find[i]=j

    if(rank_union_find[i]==rank_union_find[j] and i!=j):
        rank[j]+=1
    #如果深度相同，但是根节点不同，那么新的根节点的深度+1
    #因为如果原来的深度不同的话，合并之后根节点的深度不会增加（因为是小的合并到多的）

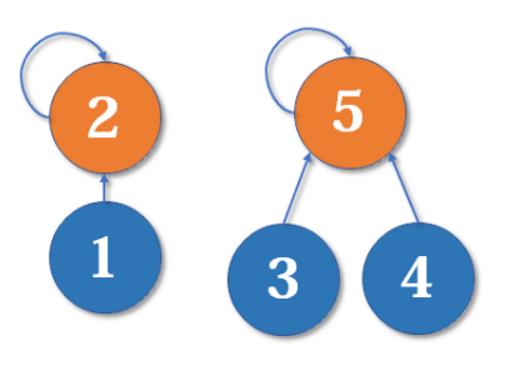
        为什么深度相同，新的根节点深度要+1？

        如下图，我们有两个深度均为2的树，现在要merge(2,5)：

        这里把2的父节点设为5，或者把5的父节点设为2，其实没有太大区别。我们选择前者，于是变成这样：

        

         显然树的深度增加了1。另一种合并方式同样会让树的深度+1。